电源完整性的PDN测试与仿真

阻抗的测量方法

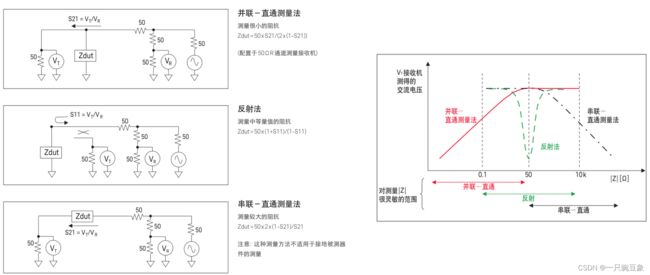
        并联直通法在小阻抗范围内具有良好的灵敏度，通常用于测量旁路电容器，这些电容在串联谐振频率附近阻抗可以低至毫欧量级，而测量阻抗较高的元器件，例如铁氧体磁珠，使用反射法则更为合理，串联直通法目前暂未涉及，从右图曲线来看，其应当更适合于信号滤波器的测量。

图片摘自：“Keysight Technologies – 使用E5061B低频-射频网络分析仪测量直流-直流转换器和PDN应用指南” 

反射法工作原理

        最简单的阻抗测试由单端口网分完成，VNA的源信号为50欧姆端接的正弦波发生器，通过传输线发射到DUT，返回探测器将拾取反射回来的正弦波，反射信号的强弱取决于DUT和50欧姆系统之间（源以及传输线）阻抗不匹配的程度；

        测量精度上，1Ω至2kΩ精度约为10%，不适用于更低阻抗的测试；

        举例说明： 当DUT阻抗为1Ω时，S11为-0.96或-0.35dB，较为合理； 当DUT阻抗为0.1Ω时，S11为-0.996或-0.035dB，这是一个非常小的反射量，已经很难将其与0Ω区分开，因此，也就不能进行更低阻抗的精准测量。

图片摘自：“Keysight Technologies – Ultra-Low Impedance Measurements Using 2-Port Measurement” 

反射法的限制区间

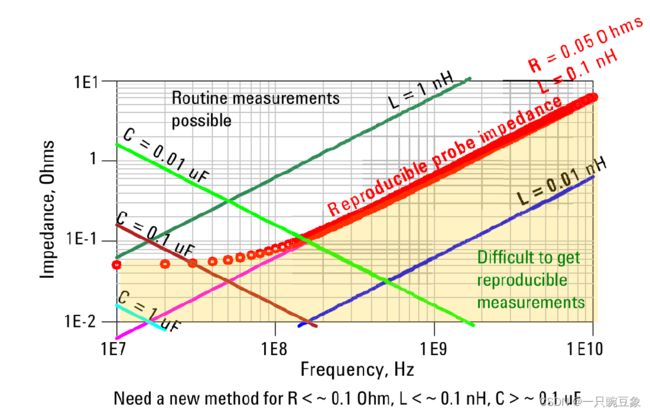
        如果考虑到电容的实际等效模型，那么单端口阻抗测试的限制点大致是：

        R < 0.1Ω，L < 0.1nH，C > 0.1uF

        当设计中临界了以上的条件，则需要引入新的阻抗测试方法。

图片摘自：“Keysight Technologies – Ultra-Low Impedance Measurements Using 2-Port Measurement”

并联-直通法工作原理

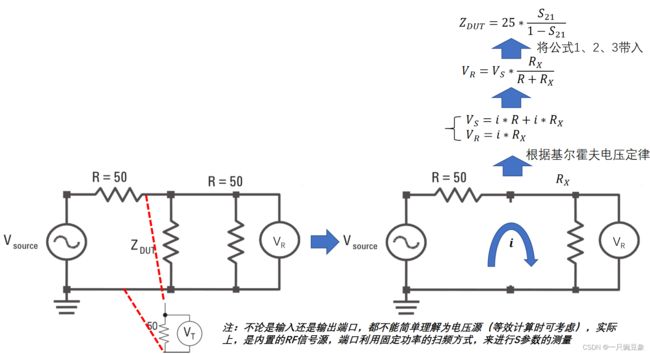
        通过将DUT并联在激励信号线和接地线之间，然后测量传输系数S21，再从S21推导出DUT的阻抗，S21表示由非常小的并联阻抗导致的很大衰减；

        假设Vsource做为VNA内部的50欧姆信号源，当其施加到VT端口时，VT端口电压为：             V_T=1/2∗V_source        --公式1

        S21表达式可以简化为：     

        S_21=V_R/V_T            --公式2

        为方便计算，对DUT和接收机的端口阻抗进行了合并：     

        R_X=Z_DUT∗R/(Z_DUT+R)        --公式3 

并联-直通法的探头连接方式

        PDN测试有三种探头的连接方式可供选择，小编最终采用了下图中的(a)选项所描述的焊接方法，但是，在实际设计中，由于芯片和电容采用了正反面放置，所以探头测试点最终选在芯片焊接植球处，图示（a）所表示的是电容与芯片在同一面时的情形，接下来，用这种方法，对所用芯片的4组0.8V供电网络进行了PDN的测试及仿真对比。 

图片摘自：“Keysight Technologies – 使用E5061B低频-射频网络分析仪测量直流-直流转换器和PDN应用指南” 

测试与仿真结果对比

        从四路的数据对比可以发现，测试与仿真的差异主要存在于谐振点的表现上：仿真可以很清楚地观察到每个电容谐振点的影响情况，而测试则不明显或存在一定的差异，这其中，电容模型与实际使用性能之间的差异、焊接带来的偏差、VNA的校准精度等都是影响测试结果的外在因素，因此，想取得完全一致的结果，有一定的困难或费时费力的，至少从目前的结果来看，基本达到了小编的预期，尤其是在谐振点之后的ESL表现形式上，几乎是相同的；

电容案例

        考虑完常温的表现，小编对高低温时的电容阻抗表现同样非常关注，举一个电容的例子，某供应商曾经提供过一颗1uF三端子电容的高低温及常温模型，对其三温的阻抗曲线进行了对比；

        从其阻抗曲线上，明显可以观察到，较之常温时，高低温时的谐振点往高频处发生偏移（因为容值变小，这样的变化也导致在进入谐振点之前的曲线斜率变得更为陡峭，当组合使用时，阻抗波动将会略为明显），过了谐振点后，伴随着感抗曲线的进一步降低（其感抗值ESL变小了）；

        如果单纯考虑该电容个体的温度性能，那么，常温会成为worst case，这也就能解释，为什么无需进行高低温的PDN仿真，那么，实际情况会是如何呢？ 

温漂影响

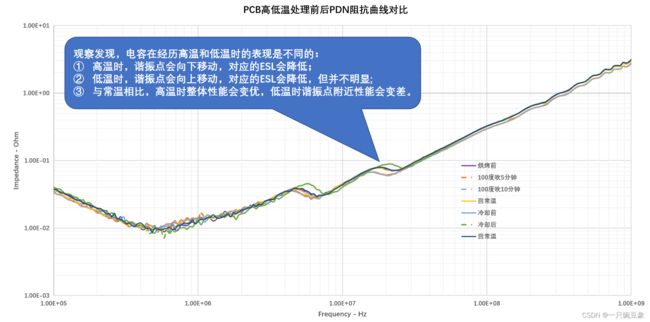
        为了验证所用电容在高低温下的PDN影响，小编用热风枪对板子上的电容进行了烘烤，然后用冷却剂进行速冻，并对结果进行了对比；

        经历的过程如下：常温-->100度烘烤5分钟-->100度烘烤10分钟-->回常温-->静置一天-->冷却至极低度-->回常温；

温漂试验数据对比 

电容温漂数据对比

        对所使用到的电容的温度系数进行了收集对比，发现与PDN相关的这些电容，在温度超过80度时，均会呈现容值下降的趋势，会导致谐振点往高频处移动，这与上一页所观察到的部分现象不相符合，尤其是高温时的曲线，所以，高温下，电容发生的应当不仅仅是容值及ESL的变化，其它外部参数，甚至板材是否会发生性能变化，都是未知的，小编暂时也未开始更为深入的调查； 

结论

        通过上述的数据汇总，可以发现，PDN的测试和仿真，可以达到较好的匹配度，仿真结果基本是可以被相信的，除此之外，在这个过程中，有一些技巧必须要被关注：

        1. 测试时，必须保证线缆焊接的牢固，而且，并联直通法要求两根线缆要焊接在同一个电源引脚，同一个地引脚上；

        2. 仿真时，需要开启过孔周围的3D网格细化功能，其会使用增强的网格质量对过孔及其周边进行二次电流计算，从而得到更为准确的阻抗计算结果，这点对于高频处的ESL计算尤为重要；

        3. 仿真中，由于有些电源网络的管脚数量太多，通常会采用等势面的计算方式，而测试中，只能是针对某一个具体管脚的阻抗测量，因此，两者会存在差异；

        4. 如果要在仿真中排除这种差异，就需要按照测试的环境，对同一个电源引脚，同一个地引脚进行单独的仿真运算；

        5. 通常情况下，仿真会采用等势面的计算方式，主要是因为，在BGA内部设计中，其电源采用的也是一个完整的平面，而所有的电源引脚会统一接到这一平面上，并且，完整平面会导致感抗的进一步降低以及容抗的进一步提升，因而，等势面计算的结果会优于单引脚计算的结果（小编之前也与做芯片仿真的同行交流过，大概也是这个原因，如理解有误，欢迎指正）；

        6. 由于有太多的外在限制因素，比如焊接带来的寄生参数、线缆的校准好坏、电容模型与实际参数的差异、仿真与实际板材信息的差异等等，仿真与测量不可能得到一模一样的结果，但是，只要趋势上能够吻合，尤其是电容的谐振变化能够达到趋势上的一致性，仿真就达到了参考的价值；

        7. 温度对PDN的影响是综合因素的产物，单纯从电容个体进行考虑，其性能不会变差，但是组合使用后，高低温就产生了不同的效果，相对来说，低温更值得被关注，如果想进行三温的仿真评估，就不得不要求供应商提供更多的参数模型，但是板材的温度变化影响暂时不能在仿真中得到体现。