数据结构（7.5）-- 树扩展之字典树

一、字典树

1、字典树介绍

字典树，也称为“前缀树”，是一种特殊的树状数据结构，对于解决字符串相关问题非常有效。典型

用于统计、排序、和保存大量字符串。所以经常被搜索引擎系统用于文本词频统计。它的优点是：

利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树

高。

2、字典树的性质

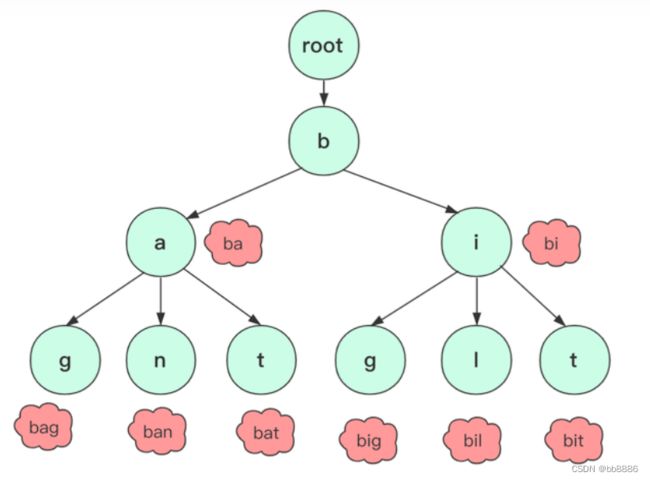
（1）根节点不包含字符，除了根节点每个节点都只包含一个字符。root节点不含字符这样做的目的是为了能够包括所有字符串。

（2）从根节点到某一个节点，路过字符串起来就是该节点对应的字符串。

（3）每个节点的子节点字符不同，也就是找到对应单词、字符是唯一的。

3、字典树的实现

(1)定义多叉树--孩子表示法

struct TreeNode {
    ELEMENT_TYPE value;    //结点值
    TreeNode* children[NUM];    //孩子结点
};

(2) 定义字典树

int size = 26;
struct TrieNode {
    bool isEndOfWord; //记录该结点是否是一个串的结束
    TrieNode* children[SIZE]; //字母映射表
};

二、面试中关于字典树的常见问题

1、计算字典树中的总单词数

题目：创建一颗字典树，并且计算该字典树中的总单词数。如下字典树，[“bag”， “ban”， “bat”， “big”，“bil”，“bit”]，单词数为6。

思路：

首先要创建一颗字典树，在每个节点上，设置一个标记来表示该节点是否是一个单词的结束。

再向字典树中插入单词，从根节点开始，递归地遍历字典树的所有子节点。

最后计算单词数：对于每个子节点，如果其标记为结束，则将计数器加1。最终，计数器的值就是字典树中的总单词数。

#include
using namespace std;

const int ALPHABET_SIZE = 26;
// TrieNode表示字典树中的节点
struct TrieNode
{
    bool isEndOfWord; //用于标记该节点是否是一个单词的结束
    TrieNode* children[ALPHABET_SIZE]; //包含26个子节点的数组
    // 构造函数
    TrieNode():isEndOfWord(false){
        for(int i = 0; i < ALPHABET_SIZE; i++){
            children[i] = nullptr;
        }
    }
};

class Trie{
    private:
        TrieNode* root;
    public:
        Trie(){
            root = new TrieNode();
        }
        // 向字典树中插入单词
        void insert(string word){
            TrieNode* current = root;
            // 遍历字符串中的字符
            for(char ch: word){
                int index = ch - 'a';
                if(current->children[index] == nullptr)
                    current->children[index] = new TrieNode();
                current = current->children[index];
            }
            // 遍历结束，标记该节点单词结束
            current->isEndOfWord = true;
        }
        // 计算字典树中的总单词数
        int countWords(){
            int count = 0;
            countWordsDFS(root, count);
            return count;
        }

    private:
        // 深度优先搜索（DFS）递归地遍历字典树的所有节点，并在遇到结束节点时将计数器加1。
        void countWordsDFS(TrieNode* node, int& count){
            if(node == NULL)
                return;
            if(node->isEndOfWord) 
                count += 1;
            for(int i = 0; i < ALPHABET_SIZE; i++){
                if(node->children[i] != NULL)
                    countWordsDFS(node->children[i], count);
            }
        }

};


int main(){
   Trie trie;
   trie.insert("bag");
   trie.insert("ban");
   trie.insert("bat");
   trie.insert("big");
   trie.insert("bil");
   trie.insert("bit");
   
   int count = trie.countWords();
   cout << "字典树中的总单词数：" << count << endl;
}

2、查找字典树中某个单词是否存在 

题目：输入ban，返回true；输入bad，返回False。

思路：和插入操作类似。

从字典树的根节点依次遍历单词中的字符，如果当前节点的子节点中，不存在键为 ch 的节点，则说明不存在该单词，直接返回 False。如果当前节点的子节点中，存在键为 ch 的节点，则令当前节点指向新建立的节点，然后继续查找下一个字符。在单词处理完成时，判断当前节点是否有单词结束标记，如果有，则说明字典树中存在该单词，返回 True。否则，则说明字典树中不存在该单词，返回 False。

#include
using namespace std;

const int ALPHABET_SIZE = 26;
// TrieNode表示字典树中的节点
struct TrieNode
{
    bool isEndOfWord; //用于标记该节点是否是一个单词的结束
    TrieNode* children[ALPHABET_SIZE]; //包含26个子节点的数组
    // 构造函数
    TrieNode():isEndOfWord(false){
        for(int i = 0; i < ALPHABET_SIZE; i++){
            children[i] = nullptr;
        }
    }
};

class Trie{
    private:
        TrieNode* root;
    public:
        Trie(){
            root = new TrieNode();
        }
        // 向字典树中插入单词
        void insert(string word){
            TrieNode* current = root;
            // 遍历字符串中的字符
            for(char ch: word){
                int index = ch - 'a';
                if(current->children[index] == nullptr)
                    current->children[index] = new TrieNode();
                current = current->children[index];
            }
            // 遍历结束，标记该节点单词结束
            current->isEndOfWord = true;
        }
        // 查找字典树中某个单词是否存在
        bool searchWord(string word){
            TrieNode* current = root;
            for(char ch: word){
                int index = ch - 'a';
                if(current->children[index] == NULL)
                    return false; //如果当前节点的子节点中，不存在键为 ch 的节点,直接返回false
                current = current->children[index];
            }
            // 判断当前节点是否为空，并且是否有单词结束标记
            return (current->isEndOfWord & current != NULL);
        }

};


int main(){

    Trie trie;
    trie.insert("bag");
    trie.insert("ban");
    trie.insert("bat");
    trie.insert("big");
    trie.insert("bil");
    trie.insert("bit");
   string word = "bad";
    bool b = trie.searchWord(word);
    if(b)
        cout << "该字典树存在" << word;
    else
        cout << "该字典树不存在" << word;

}

3、查找字典树中某个前缀是否存在

在字典树中查找某个前缀是否存在，和字典树的查找单词操作一样，不同点在于最后不需要判断是否有单词结束标记。

// 查找字典树中某个前缀是否存在
        bool searchWord(string word){
            TrieNode* current = root;
            for(char ch: word){
                int index = ch - 'a';
                if(current->children[index] == NULL)
                    return false; //如果当前节点的子节点中，不存在键为 ch 的节点,直接返回false
                current = current->children[index];
            }
            // 判断当前节点是否为空
            return current;
        }

4、打印存储在字典树中的所有单词

题目：如下字典树，打印[ bag，ban，bat，big，bil，bit ]。

思路：在哈希遍历树的完整路径中，我们使用先序遍历逐步构建叶子节点的路径。本题类似，使用

深度遍历递归地遍历字典树的所有子节点，并存储每个叶子节点的字符串。遇到叶子节点（即

isEndOfWord=true），则打印存储在容器里的字符串（字符串组合起来就是一个完整单词）。

#include
using namespace std;

const int ALPHABET_SIZE = 26;
// TrieNode表示字典树中的节点
struct TrieNode
{
    bool isEndOfWord; //用于标记该节点是否是一个单词的结束
    TrieNode* children[ALPHABET_SIZE]; //包含26个子节点的数组
    // 构造函数
    TrieNode():isEndOfWord(false){
        for(int i = 0; i < ALPHABET_SIZE; i++){
            children[i] = nullptr;
        }
    }
};

class Trie{
    private:
        TrieNode* root;
    public:
        Trie(){
            root = new TrieNode();
        }
        // 向字典树中插入单词
        void insert(string word){
            TrieNode* current = root;
            // 遍历字符串中的字符
            for(char ch: word){
                int index = ch - 'a';
                if(current->children[index] == nullptr)
                    current->children[index] = new TrieNode();
                current = current->children[index];
            }
            // 遍历结束，标记该节点单词结束
            current->isEndOfWord = true;
        }
        void printWord(){
            string arr;
            print(root, arr);
        }
    private: 
        void print(TrieNode* node, string& arr){
            
            if(node->isEndOfWord){
                for(auto a: arr)
                    cout << a;
                cout << "," ;
                }
              
            for(int i = 0; i < ALPHABET_SIZE; i++){
                if(node->children[i] != NULL){
                    char ch = i + 'a';
                    arr.push_back(ch);
                    print(node->children[i], arr);
                }
            }
            arr.pop_back();
        }
};


int main(){
   Trie trie;
   trie.insert("bag");
   trie.insert("ban");
   trie.insert("bat");
   trie.insert("big");
   trie.insert("bil");
   trie.insert("bit");
   
   trie.printWord();
}

 

5、使用字典树对数组的元素进行排序

题目：

input：arr = ['apple', 'banana', 'application']

output：arr = ['apple', 'application', 'banana']

思路：同第二题，因为字典树节点的顺序已经确定，所以，遍历出来的单词即是排序后的单词组。

#include
#include
using namespace std;

const int ALPHABET_SIZE = 26;
// TrieNode表示字典树中的节点
struct TrieNode
{
    bool isEndOfWord; //用于标记该节点是否是一个单词的结束
    TrieNode* children[ALPHABET_SIZE]; //包含26个子节点的数组
    // 构造函数
    TrieNode():isEndOfWord(false){
        for(int i = 0; i < ALPHABET_SIZE; i++){
            children[i] = nullptr;
        }
    }
};

class Trie{
    private:
        TrieNode* root;
    public:
        Trie(){
            root = new TrieNode();
        }
        // 向字典树中插入单词
        void insert(string word){
            TrieNode* current = root;
            // 遍历字符串中的字符
            for(char ch: word){
                int index = ch - 'a';
                if(current->children[index] == nullptr)
                    current->children[index] = new TrieNode();
                current = current->children[index];
            }
            // 遍历结束，标记该节点单词结束
            current->isEndOfWord = true;
        }
        vector Order(){
            string arr;
            vector s;
            traverse(root, arr, s);
            return s;
        }
    private: 
    // arr:连接字符串组成的单词，res：排序后的数组
        void traverse(TrieNode* node, string& arr, vector& res){
            
            if(node->isEndOfWord){
                res.push_back(arr);
                }
              
            for(int i = 0; i < ALPHABET_SIZE; i++){
                if(node->children[i] != NULL){
                    char ch = i + 'a';
                    arr.push_back(ch);
                    traverse(node->children[i], arr, res);
                }
            }
            arr.pop_back();
        }
};


int main(){
   Trie trie;
   vector arr = { "apple", "banana", "application" };
    for (const string& word : arr)
        trie.insert(word);
   
   vector sortedArr = trie.Order();
   std::cout << "排序后的数组元素：" << std::endl;
    for (const std::string& word : sortedArr)
        std::cout << word << std::endl;
}