百钱百鸡-第11届蓝桥杯选拔赛Python真题精选

[导读]：超平老师的Scratch蓝桥杯真题解读系列在推出之后，受到了广大老师和家长的好评，非常感谢各位的认可和厚爱。作为回馈，超平老师计划推出《Python蓝桥杯真题解析100讲》，这是解读系列的第14讲。

百钱百鸡，本题是2019年~2020年举办的第11届蓝桥杯青少组Python编程选拔赛真题（具体日期不详），题目要求编程解决经典的百钱百鸡问题，即拿100元钱买100只鸡，可以买到公鸡、母鸡和小鸡各多少只。

先来看看题目的要求吧。

一.题目说明

背景信息：

我国古代数学家张丘建（公元五世纪，南北朝时期）在《算经》一书中最早提出了不定方程组的数学问题，原文为：鸡翁一值钱五，鸡母一值钱三，鸡维三值钱一。

百钱买百鸡，问鸡翁、鸡母、鸡维各几何？

编程实现：

上述问题即：拿100 元钱买 100 只鸡。如果公鸡 5 元一只，母鸡 3 元一只，小鸡仔 1元3只，应该各买多少只？

请编程求解，输出所有可能的答案。

输入描述：

无

输出描述：

输出所有的答案；要求一行品示一组答案，分行输出所有的答案。输出样例如下：

公鸡XX只，母鸡XX只，小鸡仔XX只

公鸡XX只，母得XX只，小鸡仔XX只

评判标淮：

• 6 分：至少能输出一组正确的答案，输出格式不需要符合样例；

• 5分：至少能输出一组正确的答案，且输出格式符合样例；

• 9分：分行输出所有正确的答案，且输出格式符合样例。

二.思路分析

这是一道经典的计算题，考查的知识点包括枚举算法、循环嵌套和条件语句。

百钱百鸡是一道经典的数学问题，在数学中，一般会使用列方程的方式来求解。

假设公鸡数量为x，母鸡数量为y，小鸡数量为z，如图：

可以得到如下方程式组：

5x + 3y + z/3 = 100x + y + z = 100

其中x、y、z的值范围都是0~100，包括0和100。

很显然，这里有3个未知数，但是只有两个方程式，所以这是一个不定方程，其解有多组。

对于有多组解的不定方程，需要使用猜解的方式，所谓猜解，就是逐个列举，找到满足方程式的解，这其实就是枚举法。

对于计算机来说，枚举是它的强项，所以，我们可以使用枚举算法来解决。

如果只是想得到问题的解，代码是比较简单的。但是，对于算法的具体实现，不同的同学可能会有不同的见解，自然也会有不同的写法。

如何写出算法效率更高的代码，也是我们需要考虑的一个问题。

思路有了，接下来，我们就进入具体的编程实现环节。

三.编程实现

根据上面的思路分析，我们分两步来编写程序：

• 简单实现

• 逐步优化

1. 简单实现

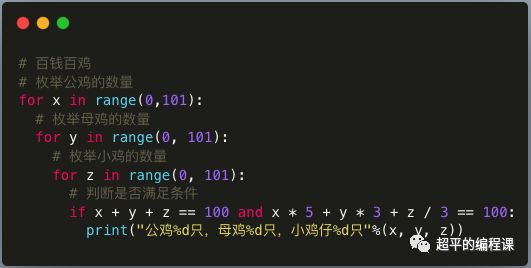
根据前面的思路分析，我们用一个最简单粗暴的方式来编写代码，如下：

代码非常简单，运行程序，效果如下：

从结果上来看，没有任何问题，但是从效率来看，这个代码就有点惨不忍睹啦，所以我们需要进行优化，提升算法的效率。

如何考量算法的效率呢，最常用的就是时间复杂度，也就是所谓的大O表示法。简单来说，就是程序执行的次数。

那你知道上面的程序，重复执行了多少次吗？

一共是101 * 101 * 101 =  1030301次，不经意间就已经百万级别了，是不是感觉怪吓人的。

2.逐步优化

在上面的循环中，我们的变量x、y、z的范围都是0~100，实际上，母鸡的数量最多只有100//5 = 20，公鸡的数量最多只有 100//3 = 33只，而小鸡的数量最多有100 * 3 = 300只。

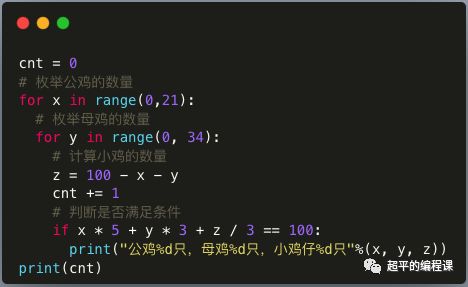
稍作修改，代码如下：

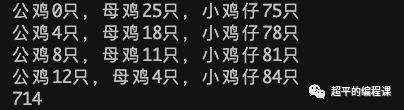
代码中增加了一个变量cnt，用于统计循环的次数，运行程序，如下：

结果一样，cnt的值为214200，这说明循环次数由原来的100万降低到21万，效率提升了80%。

还可以继续优化，之所以次数较多，主要是因为嵌套了3层循环，能否减少一层呢？

完全可以，既然已经知道公鸡有x只，母鸡有y只，那么小鸡就是（100 - x - y）只了，这样就可以将3层循环简化为两层循环。

相应的代码如下：

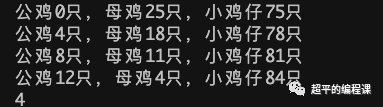
运行程序，结果如下：

这一次循环次数只有714，和21万相比，效率提升了300倍，和最初的100万相比，效率提升了1400倍！

优化到这里，就已经非常好了，但是从算法的角度来讲，还是有继续优化的空间。

还记得前面列出的方程式吧：​​​​​​​

5x + 3y + z/3 = 100x + y + z = 100

如果将这里的z消掉，只保留x和y的值，可以得到如下方程式：

y = 25 - 7/4 * x

这里的y表示母鸡的数量，肯定是大于等于0的整数，这就意味着：

25 - 7/4 * x >= 0

稍作简化，可以得到：

x <= 14

因为y是整数，也就意味着7/4 *x 是整数，所以x必须是4的倍数，这样就可以得到x的取值可以是：

0、4、8、12

因此，我们只需要一层循环即可，也不需要条件判断了，对应的代码如下：

运行程序，结果如下：

这一次，只需要执行4次，就可以了和之前的次数相比，几乎可以忽略不计了，厉害吧。

当然了，在实际答题的时候，不需要这里的cnt变量。

至此，整个程序就优化完成了，你也赶紧来试试吧。

四.总结与思考

本题的分数为20分，代码在8行左右，涉及到的知识点包括：

• 循环语句，主要是for...in循环；

• 循环嵌套的使用；

• print()函数的格式化输出；

• 枚举算法的实现及其优化；

题目难度一般，如果不考虑算法的效率，只要学过循环和选择结构，基本上都能快速地写出程序。但是，只写出程序是不够的，我们还得写出高效的程序。

实际上，在所有的编程竞赛中，当然也包括蓝桥杯，对程序的执行时间（时间复杂度）和占用空间（空间复杂度）都有明确的要求。

这就要求我们编写的程序必须满足“双低”，即低时间复杂度和低空间复杂度。

对于编程而言，所有的算法都离不开枚举，但是不能仅仅停留在暴力枚举层面，而是要思考如何聪明的枚举，如何高效的枚举，于是针对不同的问题采取了使用了不同的策略，这才产生了众多的算法。

这也要求我们在平时学习编程的时候，也要多思考一下，有没有更简单更高效的算法，这样才能快速提升自己的编程水平和算法能力。

你还有什么好的想法和创意吗，也非常欢迎和超平老师分享探讨。

如果你觉得文章对你有帮助，别忘了点赞和转发，予人玫瑰，手有余香

有需要源码的，可以移步至“超平的编程课”gzh。