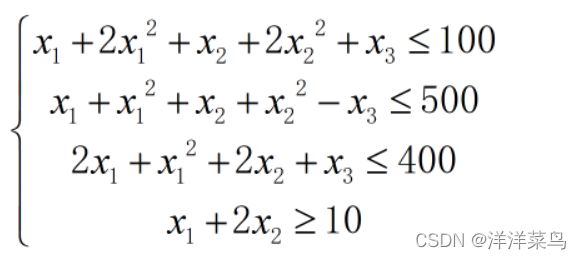蒙特卡罗模拟法 —— python

目录

1.简介

2.实例分析

2.1 模拟求近似圆周率

2.2 估算定积分

2.3 求解整数规划

---

1.简介

        蒙特卡洛又称随机抽样或统计试验，就是产生随机变量，带入模型算的结果，寻优方面，只要模拟次数够多，最终是可以找到最优解或接近最优的解。

         基本思想：为了解决数学、物理、工程技术等方面的问题，首先建立一个概率模型或随机过程，使它的参数等于问题的解；然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征，最后给出所求解的近似值。

2.实例分析

2.1 模拟求近似圆周率

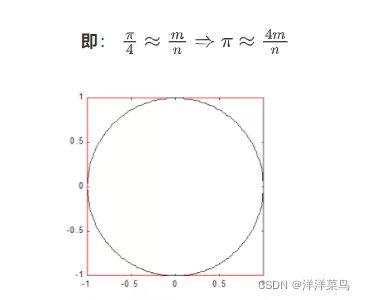
        绘制单位圆和外接正方形，正方形ABCD的面积为：2*2=4，圆的面积为：S=Π*1*1=Π，现在模拟产生在正方形ABCD中均匀分布的点n个，如果这n个点中有m个点在该圆内，则圆的面积与正方形ABCD的面积之比可近似为m/n

程序如下：

#模拟求近似圆周率
import random
import numpy as np
import matplotlib.pyplot as plt
#解决图标题中文乱码问题
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
#进入正题
r=random.random()
num=range(0,200000,10)
mypi=np.ones((1,len(num)))
for j in range(len(num)):
    # 投点次数
    n = 10000
    # 圆的半径、圆心
    r = 1.0
    a,b = (0.,0.)
    # 正方形区域
    x_min, x_max = a-r, a+r
    y_min, y_max = b-r, b+r
    # 在正方形区域内随机投点
    x = np.random.uniform(x_min, x_max, n) #均匀分布
    y = np.random.uniform(y_min, y_max, n)
    #计算点到圆心的距离
    d = np.sqrt((x-a)**2 + (y-b)**2)
    #统计落在圆内点的数目
    res = sum(np.where(d < r, 1, 0))
    #计算pi的近似值（Monte Carlo:用统计值去近似真实值）
    mypi[0,j] = 4 * res / n
plt.plot(range(1,len(mypi[0])+1),mypi[0],'.-') 
plt.grid(ls=":",c='b',)#打开坐标网格
plt.axhline(y=np.pi,ls=":",c="yellow")#添加水平直线
# plt.axvline(x=4,ls="-",c="green")#添加垂直直线
plt.legend(['模拟', '实际'], loc='upper right', scatterpoints=1)
plt.title("近似圆周率")
plt.show()

返回：

2.2 估算定积分

程序如下：

#估算定积分
import random
import numpy as np
import matplotlib.pyplot as plt
#解决图标题中文乱码问题
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
#进入正题
r=random.random()
num=range(1,10**6,500)
s = np.ones((1,len(num)))
for j in range(len(num)):
    n = 30000
    #矩形边界区域
    x_min, x_max = 0.0, 1.0
    y_min, y_max = 0.0, 1.0
    #在矩形区域内随机投点x
    x = np.random.uniform(x_min, x_max, n)#均匀分布
    y = np.random.uniform(y_min, y_max, n)
    #统计落在函数y=x^2下方的点
    res = sum(np.where(y < x**2, 1 ,0))
    #计算定积分的近似值
    s[0,j] = res / n
plt.plot(range(1,len(s[0])+1),s[0],'.-') 
plt.grid(ls=":",c='b',)#打开坐标网格
plt.axhline(y=1/3,ls=":",c="red")#添加水平直线
# plt.axvline(x=4,ls="-",c="green")#添加垂直直线
plt.legend(['模拟', '实际1/3'], loc='upper right', scatterpoints=1)
plt.title("估算定积分")
plt.show()

返回：

2.3 求解整数规划

要解的方程为：

条件如下：

程序如下：

# 求解整数规划
import random
import numpy as np
import time
import matplotlib.pyplot as plt
#解决图标题中文乱码问题
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
#进入正题
time_start=time.time() #计时开始
p0=0
for i in range(10**7):
    x=np.random.randint(0,99,(1,3))
    f=2*x[0,0]+3*x[0,0]**2+3*x[0,1]+x[0,1]**2+x[0,2]
    g=[
        x[0,0]+2*x[0,0]**2+x[0,1]+2*x[0,1]**2+x[0,2],
        x[0,0]+x[0,0]**2+x[0,1]+x[0,1]**2-x[0,2],
        2*x[0,0]+x[0,0]**2+2*x[0,1]+x[0,2],
        x[0,0]+2*x[0,1]**2
    ]
    if g[0]<=100 and g[1]<=500 and g[2]<=400 and g[3]>=10:
        if p0

返回：