第3章 表、栈和队列
前言
本章讨论最简单和最基本的三种数据结构。实际上，每一个有意义的程序都将至少明确使用一种这样的数据结构，而栈则在程序中总是隐含使用，不管你在程序中是否做了声明。
在这一章，我们将：
- 介绍抽象数据类型(ADT)的概念。
- 阐述如何对表进行有效的操作。
- 介绍栈ADT及其在实现递归方面的应用。
- 介绍队列ADT及其在操作系统和算法设计中的应用。
因为这些数据结构非常重要，所以有人可能会以为它们很难实现。事实上，它们极容易编程，主要的困难是要做足够的训练，以便写出一般只有几行大小的好的通用例程。
3.1 抽象数据类型
程序设计的基本法则之一是例程不应超过一页。这可以通过把程序分割为一些模块(module)来实现。每个模块是一个逻辑单位并执行某个特定的任务，它通过调用其他模块而使本身保持很小。模块化有几个优点。第一，调试小程序比调试大程序要容易得多。第二，多个人同时对一个模块化程序编程要更容易。第三，一个写得好的模块化程序把某些依赖关系只局限在一个例程中，这样使得修改起来更容易。例如，需要以某种格式编写输出，那么重要的当然是让一个例程去实现它。如果打印语句分散在程序各处，那么修改所费的时间就会明显地拖长。全局变量和副作用是有害的观念也正是出于模块化是有益的想法。
抽象数据类型(Abstract Data Type，ADT)是一些操作的集合。抽象数据类型是数学的
抽象，在ADT的定义中根本没涉及如何实现这些操作。这可以看作模块化设计的扩充。
例如表、集合、图以及它们的操作，它们都可以看作抽象数据类型，就像整数、实数和布尔量是数据类型一样。整数、实数及布尔量有与它们相关的操作，而抽象数据类型也有与之相关的操作。对于集合ADT，我们可以有并(union)、交(intersection)、求大小(size)以及取余(complement)等操作。或者，我们也可以只要两种操作——并和查找(find)，这两种操作又在该集合上定义了一种不同的ADT。
我们的基本的想法是，这些操作的实现只在程序中编写一次，而程序中任何其他部分需要在该ADT上运行其中的一种操作，都可以通过调用适当的函数来进行。如果由于某种原因需要改变操作的细节，通过只修改运行这些ADT操作的例程应该可以很容易实现。在理想的情况下，这种改变对于程序的其余部分通常是完全透明的。
对于每种ADT并不存在什么法则来告诉我们必须要有哪些操作，这是一个设计决策。错误处理和关系的重组(在适当的地方)一般也取决于程序设计者。我们在本章中将要讨论的这三种数据结构是ADT的最基本的例子。我们将会看到它们中的每一种是如何以多种方法实现的，不过，使用它们的程序却没有必要知道它们是如何正确实现的。
3.2 表ADT
我们将处理形如
的普通表。这个表的大小是N。我们称大小为0的表为空表(empty list)。
对于除空表外的任何表，我们说
后继
(或继之后)并称
(
)前驱(
)。表中的第一个元素是
，而最后一个元素是
。我们将不定义的前驱元，也不定义的后继元。元素在表中的位置为
。为了简单起见，我们在讨论中将假设表中的元素是整数，但一般说来任意的复元素也是允许的。
与这些“定义”相关的是我们要在表ADT上进行的操作的集合。PrintList和MakeEmpty是常用的操作，其功能显而易见；Find返回关键字首次出现的位置：Insert和Delete一般是从表的某个位置插入和删除某个关键字；而Findkth则返回某个位置上(作为参数指定)的元素。如果34，12，52，16，12是一个表，则Find(52)会返回3；Insert(X，3)可能把表变成34，12，52， X，16，12(如果在给定位置的后面插入的话)；而Delete(52)则将该表变为34，12，X，16，12。
当然，一个函数的功能怎样才算恰当，完全要由程序设计员来确定，就像对特殊情况的处理那样。(例如，上述Find(1)返回什么？)我们还可以添加一些运算，比如Next和previous，它们会取一个位置作为参数并分别返回其后继元和前驱元的位置。
3.2.1 表的简单数组实现
对表的所有操作都可以使用数组来实现。虽然数组是动态指定的，但还是需要对表的大小的最大值进行估计。通常需要估计得大一些，而这会浪费大量的空间。这是严重的局限，特别是在存在许多未知大小的表的情况下。
数组实现使得PrintList和Find正如所预期的那样以线性时间执行，而Findkth则花费常数时间。然而，插入和删除的花费是昂贵的。例如，在位置0的插入(这实际上是插入一个新的第一元素)首先需要将整个数组后移一个位置以空出空间来，而删除第一个元素则需要将表中的所有元素前移一个位置，因此这两种操作的最坏情况为
。平均来看，这两种运算都需要移动表中一半的元素，因此仍然需要线性时间。只通过
次相继插入来建立一个表将需要二次时间。
因为插入和删除的运行时间非常慢并且表的大小还必须事先已知，所以简单数组一般不用来实现表这种结构。
3.2.2 链表
为了避免插入和删除的线性开销，我们允许表可以不连续存储，否则表的部分或全部需要整体移动。图3-1表达了链表(linked list)的一般想法。
链表由一系列不必在内存中相连的结构组成。每一个结构均含有表元素和指向包含该元素后继元的结构的指针。我们称之为Next指针。最后一个单元的Next指针指向NULL；该值由C定义并且不能与其他指针混淆。ANSIC规定NULL为零。
指针变量就是包含存储另外某个数据的地址的变量。因此，如果P被声明为指向一个结构的指针，那么存储在P中的值就被解释为主存中的一个位置，在该位置能够找到一个结构。该结构的一个域可以通过P->FieldName访问，其中FieldName是我们想要考察的域的名字。图3-2指出图3-1中表的具体表示。这个表含有五个结构，恰好在内存中分配给它们的位置分别是1000、800、712、992和692。第一个结构的指针含有值800，它提供了第二个结构所在的位置。其余每个结构也都有一个指针用于类似的目的。当然，为了访问该表，我们需要知道在哪里能够找到第一个单元。指针变量就用于这个目的。重要的是要记住，一个指针就是一个数。本章其余部分将用箭头画出指针以便直观表述。
为了执行PrintList(L)或Find(L，Key)，我们只要将一个指针传递到该表的第一个元素，然后用一些Next指针遍历该表即可。这种操作显然是线性时间的，虽然这个常数可能会比用数组实现时大。
FindKth操作不如数组实现的效率高，FindKth(L，i)操作花费
时间以显性方式遍历链表。在实践中这个界是保守的，因为调用FindKth常常是以(按)排序的方式进行。例如，FindKth(L，2)、FindKth(L，3)、FindKth(L，4)以及FindKth(L，6)可通过对表的一次扫描同时实现。
删除命令可以通过修改一个指针来实现。图3-3给出在原表中删除第三个元素的结果。
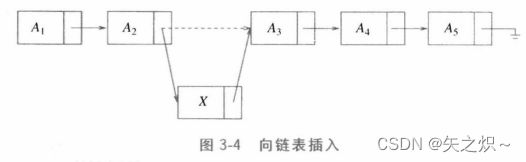
插入命令需要使用一次malloc调用从系统中得到一个新单元(后面将详细论述)并在
此后执行两次指针调整。其一般想法在图3-4中给出，其中的虚线表示原来的指针。
3.2.3 程序设计细节
上面的描述实际上足以使每一部分都能正常工作，但还是有几处地方可能会出问题。第一，并不存在从所给定义出发在表的起始端插入元素的真正显性的方法。第二，从表的起始端实行删除是一个特殊情况，因为它改变了表的起始端，编程中的疏忽将会造成表的丢失。第三个问题涉及一般的删除。虽然上述指针的移动很简单，但是删除算法要求我们记住被删除元素前面的表元。
稍做一个简单的变化就能够解决上述三个问题。我们将留出一个标志节点，有时
候称之为表头(header)或哑节点(dummy node)。这是一种惯例，在后面将会多次使用。我们约
定，表头在位置0处。图3-5表示一个带有表头的链表，它表示表
。
为避免删除操作相关的一些问题，我们需要编写例程Findprevious，它将返回我们要删除的表元的前驱元的位置。如果我们使用表头，那么当我们删除表的第一个元素时，FindPrevious将返回表头的位置。还是在这里使用它，这完全因为它使我们能够表达基本的指针操作且又不致使特殊情形的代码含混不清。除此之外，要不要使用表头则是属于个人兴趣的问题。
例如，我们将把这些表ADT的半数例程编写出来。首先，在图3-6中给出我们需要的声明。按照C的约定，作为类型的List(表)和Position(位置)以及函数的原型都列在所谓的.h头文件中。具体的Node(节点)声明则在.c文件中。
我们将编写的第一个函数用于测试空表。当我们编写涉及指针的任意数据结构的代码时，最好是先画出一张图。图3-7就表示一个空表，按照这个图，很容易写出图3-8中的函数。
下一个函数如图3-9所示，它测试当前的元素是否是表的最后一个元素，假设这个元素是存在的。
#ifndef _List_H
struct Node;
typedef struct Node *PtrToNode;
typedef struct PtrToNode List;
typedef struct PtrToNode Position;
List MakeEmpty( List L );
int IsEmpty( List L );
int IsLast( Position P, List L );
Position Find( ElementType X, List L );
void Delete( ElementType X, List L );
Position FindPrevious( ElementType X, List L );
void Insert( ElementType X, List L, Position P );
void DeleteList( List L );
Position Header( List L );
Position First( List L );
Position Advance( Position P );
ElementType Retrieve( Position P );
#endif /* _List_H */
struct Node
{
ElementType Element;
Position Next;
};
int IsEmpty(List L)
{
return L->Next == NULL;
}
int IsLast(Position P, List L)
{
return P->Next == NULL;
}
我们要写的下一个例程是Find。Find在图3-10中示出，它返回某个元素在表中的位
置。第2行用到与(&&)操作走了捷径，即如果与运算的前半部分为假，那么结果就自动为
假，而后半部分则不再执行。
Position Find(ElementType X, List L)
{
Position P;
P = L->Next;
while(P != NULL && P->Element != X)
P = P->Next;
return P;
}
递归地编写Find例程是一个非常糟糕的想法，要不惜一切代价避免它。
第四个例程是删除表L中的某个元素X。我们需要决定：如果X出现不止一次或者根本就没有，那么该做些什么？我们的例程将删除第一次出现的X，如果X不在表中我们就什么也不做。为此，我们通过调用Findprevious函数找出含有X的表元的前驱元P。实现删除(Delete)例程的程序如图3-11中所示。FindPrevious例程类似于Find，它在图3-12中列出。
void Delete(ElementType X, List L)
{
Position P, TmpCell;
P = FindPrevious(X, L);
if(!IsLast(P, L))
{
TmpCell = P->Next;
P->Next = TmpCell->Next;
free(TmpCell);
}
我们要写的最后一个例程是插入(Insert)例程。将要插入的元素与表L和位置P一起传入。这个Insert例程将一个元素插到由P所指示的位置之后。这个决定有随意性，它意味着插入操作如何实现并没有完全确定的规则。很有可能将新元素插入位置P处(即在位置P处当时的元素的前面)，但是这么做则需要知道位置P前面的元素。它可以通过调用FindPrevious而得到。因此重要的是要说明你要干什么。图3-13完成这些任务。
Position FindPrevious(ElementType X, List L)
{
Position P;
P = L;
while (P->Next != NULL && P->Next->Element != X)
P = P->Next;
return P;
}
void Insert(ElementType X, List L, Position P)
{
Position TmpCell;
TmpCell = malloc(sizeof(struct Node));
if(TmpCell == NULL)
FatalError("Out of space!");
TmpCell->Element = X;
TmpCell->Next = P->Next;
P->Next = TmpCell;
}
已经把表L传递给Insert例程和IsLast例程，尽管它从未被使用过.因为别的实现方法可能会需要这些信息，因此，若不传递表L有可能使得使用ADT的想法失败。
除Find和Findprevious例程外(还有例程Delete，它调用Findprevious)，已经编码的所有操作均需O(1)时间。这是因为在所有的情况下，不管表有多大，都只执行固定数目的指令。对于例程Find和FindPrevious，在最坏的情形下运行时间是O(N)，因为此时若元素未找到或位于表的末尾则可能遍历整个表。平均来看，运行时间是O(N)，因为必须平均扫描半个表。
3.2.4 常见的错误
最常遇到的错误是你的程序因来自系统的棘手的错误信息而崩溃，比如“memory access violation”或“segmentation violation”，这种信息通常意味着有指针变量包含了伪地址，一个通常的原因是初始化变量失败。无论何时只要确定一个指向，那么就必须保证该指针不是NULL。有些C编译器隐式地为你做这种检查，
第二种错误涉及何时使用或何时不使用malloc来获取一个新的单元。声明指向一个结构的指针并不创建该结构，而只是给出足够的空间容纳结构可能会使用的地址。创建尚未被声明过的记录的唯一方法是使用malloc库函数。malloc(HowManyBytes)奇迹般地使系统创建一个新的结构并返回指向该结构的指针。另一方面，如果你想使用一个指针变量沿着一个表行进，那就没有必要创建新的结构，此时不宜使用malloc命令。非常老的编译器需要一个类型转换(type cast)使得赋值操作符两边相符。C库提供了malloc的其他形式，如calloc。这两个例程都要求包含stdlib.h头文件。
当有些空间不再需要时，你可以用free命令通知系统来回收它。free(P)的结果是：P正在指向的地址没变，但在该地址处的数据此时已无定义了。
如果你从未对一个链表进行过删除操作，那么调用malloc的次数应该等于表的大小，若有表头则再加1。少一点儿你就不可能得到一个正常运行的程序；多一点儿你就会浪费空间并可能要浪费时间。偶尔会出现下列情况：当你的程序使用大量空间时，系统可能不能满足你对新单元的要求。此时返回的是NULL指针。
在链表中进行一次删除之后，再将该单元释放通常是一个好的想法，特别是当许多的插入和删除操作掺杂在一起而内存会出现问题的时候。对于要被释放的单元，应该需要一
个临时的变量，因为在撤除指针的工作结束后，你将不能再引用它。例如，图3-14的代码
就不是删除整个表的正确的方法(虽然在有些系统上它能够运行)。
图3-15显示了删除表的正确方法。处理闲置空间的工作未必很快完成，因此你可能要检查看看是否处理的例程会引起性能下降，如果是则要考虑周密。单元以相当特殊的顺序释放，这显然会引起另一个线性程序花费O(N log N)时间去处理N个单元。
警告：malloc(sizeof(PtrTbNode))是合法的，但是它并不给结构体分配足够的空间。它只给指针分配空间。
void DeleteList(List L)
{
Position P;
P = L->Next;;
L->Next = NULL;
while (P != NULL)
{
free(P);
P = P->Next;
}
}
void DeleteList(List L)
{
Position P, Tmp;
P = L->Next;;
L->Next = NULL;
while (P != NULL)
{
Tmp = P->Next;
free(P);
P = Tmp;
}
}3.2.5 双链表
有时候以倒序扫描链表很方便。标准实现方法此时无能为力，然而解决方法却很简单。只要在数据结构上附加一个域，使它包含指向前一个单元的指针即可。其开销是一个附加的链，它增加了空间的需求，同时也使得插入和删除的开销增加一倍，因为有更多的指针需要定位。另外，它简化了删除操作，因为你不再被迫使用一个指向前驱元的指针来访问一个关键字，这个信息是现成的。图3-16表示一个双链表(doubly linked list)。
3.2.6 循环链表
让最后的单元反过来直指第一个单元是一种流行的做法。它可以有表头，也可以没有表头(若有表头，则最后的单元就指向它)，并且还可以是双向链表(第一个单元的前驱元指针指向最后的单元)。这无疑会影响某些测试，不过这种结构在某些应用程序中却很流行。图3-17显示了一个无表头的双向循环链表。
3.2.7 例子
提供三个使用链表的例子。第一例是表示一元多项式的简单方法。第二例是在某些特殊情况下以线性时间进行排序的一种方法。最后，我们介绍一个复杂的例子，它说明了链表如何用于大学的课程注册。
1.多项式ADT
我们可以用表来定义一种关于一元(具有非负幂)多项式的抽象数据类型。令
，如果大部分系数非零，那么我们可以用一个简单数组来存储这些系数。然后，可以编写一些对多项式加减乘微分及其他操作的例程。此时，我们可以使用在图3-18中给出的类型声明。这时，我们就可编写进行各种不同操作的例程了，例如加法和乘法，它们在图3-19到图3-21中列出。忽略将输出多项式初始化为零的时间，则乘法例程的运行时间与两个输入多项式的次数的乘积成正比。它适合大部分项都有的稠密多项式，但如果
且
，那么运行时间就可能不可接受了。可以看出，大部分的时间都花在了乘以0和单步调试两个输入多项式中大量不存在的部分上。这是我们不愿看到的。
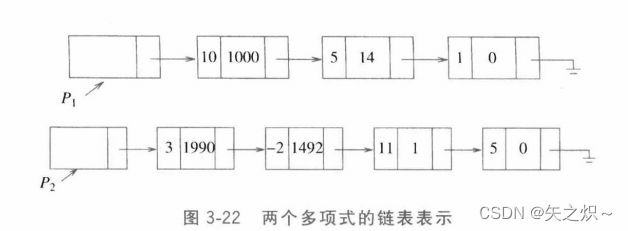
另一种方法是使用单链表(singly linked list)。多项式的每一项含在一个单元中，并且这些单元以次数递减的顺序排序。例如，图3-22中的链表表示
和
。此时我们可以使用图3-23的声明。
typedef struct
{
int CoeffArray[MaxDegree + 1];
int HighPower;
} * Polynomial;
void ZeroPolynomial(Polynomial Poly)
{
int i;
for (i = 0; i <= MaxDegree; i++)
Poly->CoeffArray[i] = 0;
Poly->HighPower = 0;
}
void AddPolynomial(const Polynomial Poly1, const Polynomial Poly2, Polynomial PolySum)
{
int i;
ZeroPolynomial(PolySum);
PolySum->HighPower = Max(Poly1->HighPower, Poly2->HighPower);
for(i = PolySum->HighPower; i >= 0; i--)
PolySum->CoeffArray[i] = Poly1->CoeffArray[i] + Poly2->CoeffArray[i];
}
void MultPolynomial(const Polynomial Poly1, const Polynomial Poly2, Polynomial PolyProd)
{
int i, j;
ZeroPolynomial(PolyProd);
PolyProd->HighPower = Poly1->HighPower + Poly2->HighPower;
if (PolyProd->HighPower > MaxDegree)
Error("Exceeded array size");
else
for (i = 0; i <= Poly1->HighPower; i++)
for (j = 0; j <= Poly2->HighPower; j++)
PolyProd->CoeffArray[i + j] += Poly1->CoeffArray[i] * Poly2->CoeffArray[j];
}
typedef struct Node *PtrToNode;
struct Node
{
int Coefficient;
int Exponent;
PtrToNode Next;
};
typedef PtrToNode Polynomial;
上述操作将很容易实现，唯一潜在的困难在于，当两个多项式相乘的时候所得到的大学生必须合并同类项，这可以有多种方法实现。
2.基数排序
使用链表的第二个例子叫作基数排序(radix sort)。基数排序有时也称为卡式排序(card sort)，因为直到现代计算机出现之前，它一直用于对老式穿孔卡的排序。
如果我们有N个整数，范围从1到M(或从0到M-1)，我们可以利用这个信息得到一种快速的排序，叫作桶式排序(bucket sort)。我们留置一个数组，称之为Count，大小为M，并初始化为零。于是，Count有M个单元(或桶)，开始时它们都是空的。当被读入时Count[]增1。在读入所有的输入以后，扫描数组Count，打印输出排好序的表。该算法花费
，如果
，则桶式排序为。
基数排序是这种方法的推广。设我们有10个数，范围在0到999之间，我们将其排序。一般说来，这是0到
间的N个数，p是某个常数。不能使用桶式排序，那样桶就太多了。我们的策略是使用多趟桶式排序。自然的算法就是通过最高(有效)“位”(对基数N所取的位)进行桶式排序，然后是对次最高(有效)位进行桶式排序，等等。这种算法不能得出正确结果，但是，如果我们用最低(有效)“位”优先的方式进行桶式排序，那么算法将得到正确结果。当然，有可能多于一个数落入相同的桶中，但有别于原始的桶式排序，这些数可能不同，因此我们把它们放到一个表中。注意，所有的数可能都有某位数字，因此如果使用简单数组表示表，那么每个数组必然大小为N，总的空间需求是
。
下面的例子说明10个数的桶式排序的具体做法。本例的输入是64，8，216，512，27，729，0，1，343，125(10个三位数，随机排列)。第一步按照最低位优先进行桶式排序。为使问题简化，此时操作按基是10进行，不过一般并不做这样的假设。图3-24显示出这些桶的位置。
为使算法能够得出正确的结果，要注意唯一出错的可能是如果两个数出自同一个桶但顺序却是错误的。不过，前面各趟排序保证了当几个数进入一个桶的时候，它们是以排序的顺序进入的。该排序的运行时间是O(P(N+B))，其中P是排序的趟数，N是要被排序的元素的个数，而B是桶数。本例中，B=N。
举一个例子，我们可以把能够在(32位)计算机上表示的所有整数按基数排序方法排序，假设我们在大小为2”的桶的条件下分三趟进行。在这台计算机上，该算法将总是O(N)的，但是，因为包含大的常数，有可能仍然不如我们将在第7章看到的某些算法有效。(注意，log N的因子并非都这么大，而该算法总有维持链表的附加开销。
3.多重表
最后一个例子阐述链表的更复杂的应用。一所由40000个学生和2500门课程的大学需要生成两种类型的报告。第一个报告列出每个班的注册者，第二个报告列出每个学生注册的班级。
常用的实现方法是使用二维数组。这样一个数组将有1亿项。平均大约一个学生注册三门课程，因此实际上有意义的数据只有120000项，约占0.1%。
现在需要的是列出每个班及每个班所包含的学生的表。我们也需要每个学生及其所注册的班级的表。图3-27显示实现的方法。
正如该图所显示的，我们已经把两个表合成为一个表。所有的表都各有一个表头并且都是循环的。比如，为了列出C3班的所有学生，我们从C3开始通过向右行进而遍历其表。第一个单元属于学生S1。虽然不存在明显的信息，但是可以通过跟踪S1链表直到该表表头而确定该生的信息。一旦找到该生信息，我们就转回到C3的表(在遍历该生的表之前，存储了我们在课程表中的位置)并找到可以确定属于S3的另外一个单元，我们继续并发现S4和S5也在该班上。对任意一名学生，我们也可以用类似的方法确定该生注册的所有课程。
使用循环表节省空间但是要花费时间。在最坏的情况下，如果第一个学生注册了每一门课程，那么表中的每一项都要检测以确定该生的所有课程名。因为在本例中每个学生注册的课程相对很少并且每门课程的注册学生也很少，最坏的情况是不可能发生的。如果怀疑会产生问题，那么每一个(非表头)单元就要有直接指向学生和班级的表头的指针。这将使空间的需求加倍，但是却简化和加速实现的过程。
3.2.8 链表的游标实现
#ifndef _Cursor_H
typedef int PtrToNode;
typedef PtrToNode List;
typedef PtrToNode Position;
void InitializeCursorSpace(void);
List MakeEmpty(List L);
int IsEmpty(const List L);
int IsLast(const Position P, const List L);
Position Find(ElementType X, const List L);
void Delete(ElementType X, List L);
Position FindPrevious(ElementType X, const List L);
void Insert(ElementType X, List L, Position P);
void DeleteList(List L);
Position Header(const List L);
Position First(const List L);
Position Advance(const Position P);
ElementType Retrieve(const Position P);
#endif /*_Cursor_H*/
struct Node
{
ElementType Element;
Position Next;
};
struct Node CursorSpace[SpaceSize];
诸如BASIC和FORTRAN等许多语言都不支持指针。如果需要链表而又不能使用指针，那么就必须使用另外的实现方法。我们将描述这种方法并称之为游标(cursor)实现法。
在链表的指针实现中有两条重要的特性：
1.数据存储在一组结构体中。每一个结构体包含数据以及指向下一个结构体的指针。
2.一个新的结构体可以通过调用malloc而从系统全局内存(globamemory)中得到，并可通过调用free而释放。
游标法必须能够模仿实现这两条特性。满足条件1的逻辑方法是要有一个全局的结构体数组。对于该数组中的任何单元，其数组下标可以用来代表一个地址。图3-28给出链表游标实现的声明。
现在我们必须模拟条件2，让CursorSpace数组中的单元代行malloc和free的职
能。为此，我们将保留一个表(即freelist)，这个表由不在任何表中的单元构成。该表
将用单元0作为表头。其初始配置如图3-29所示。
对于Next，0的值等价于NULL指针。CursorSpace的初始化是一个简单的循环结构，我们将它留作练习。为执行malloc功能，将(在表头后面的)第一个元素从freelist 中删除。为了执行free功能，我们将该单元放在freelist的前端。图3-30展示了malloc和free的游标实现。注意，如果没有可用空间，那么我们的例程可以通过置P=0正确地实现。它表明再没有空间可用，并且也可以使CursorA1loc的第二行成为空操作(no-op)。
static Position CursorAlloc(void)
{
Position P;
P = CursorSpace[0].Next;
CursorSpace[0].Next = CursorSpace[P].Next;
return P;
}
static void CursorFree(Position P)
{
CursorSpace[P].Next = CursorSpace[0].Next;
CursorSpace[0].Next = P;
}
有了这些，链表的游标实现就简单了。为了前后一致，我们的链表实现将包含一个表头节点。例如，在图3-31中，如果L的值是5而M的值为3，则L表示链表a、b、e，而M表示链表c、d、f。
为了写出用游标实现链表的这些函数，我们必须传递和返回与指针实现相同的参数。这些例程很简单。图3-32是一个测试表是否为空表的函数。图3-33实现对当前位置是否是表的末尾的测试。图3-34中的函数Find返回表L中X的位置。实现删除的程序在图3-35中给出。再有，游标实现的接口和指针实现是一样的。最后，图3-36表示Insert的游标实现。
int IsEmpty(List L)
{
return CursorSpace[L].Next == 0;
}
int IsLast(Position P, List L)
{
return CursorSpace[P].Next == 0;
}
Position Find(ElementType X, List L)
{
Position P;
P = CursorSpace[L].Next;
while (P && CursorSpace[P].Element != X)
P = CursorSpace[P].Next;
return P;
}
void Delete(ElementType X, List L)
{
Position P, TmpCell;
P = FindPrevious(X, L);
if (!IsLast(P, L))
{
TmpCell = CursorSpace[P].Next;
CursorSpace[P].Next = CursorSpace[TmpCell].Next;
CursorFree(TmpCell);
}
}
void Insert(ElementType X, List L, Position P)
{
Position TmpCell;
TmpCell = CursorAlloc();
if (TmpCell == 0)
FatalError("Out of space!!!");
CursorSpace[TmpCell].Element = X;
CursorSpace[TmpCell].Next = CursorSpace[P].Next;
CursorSpace[P].Next = TmpCell;
}
其余例程的编码类似。关键的一点是，这些例程遵循ADT的规范。它们采用特定的变量并执行特定的操作。实现对用户是透明的。游标实现可以用来代替链表实现，实际上在程序的其余部分不需要变化。由于缺少内存管理例程，因此，如果运行的Find函数相对很少，则游标实现的速度会显著加快。
freelist从字面上看表示一种有趣的数据结构。从freelist 中删除的单元是刚刚由free放入那里的单元。因此，最后放入freelist中的单元最先拿走。有一种数据结构也具有这种性质，叫作栈(stack)，它是下一节要讨论的课题。