Features and Polynomial Regression——特征与多项式回归

1.特征工程  

        特征工程（Feature Engineering）是将原始特征转化成更好的表达问题本质的特征的过程。

        例如房价预测，我们可以用这样一个线性回归模型

                                                ​

        

        其中(临界宽度)，(纵向深度)

        于是我们可以利用已有的特征创造出一个新的特征，(房子的面积size)，使用房子的面积作为特征来预测房价可能会得到更好的效果

        

2.多项式回归

2.1 为什么需要多项式回归

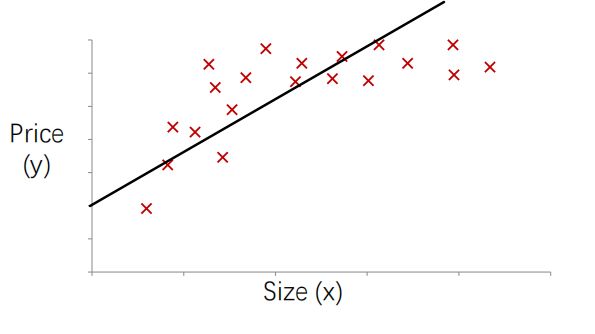
        对于一元和多元线性回归来说，特征的最高次项都为1，显然他们对于线性的数据能够有很好的拟合效果，但对于实际情况来说样本和特征值的关系更多的是非线性的，曲线才能更好的拟合，如下图，如果使用一个一次函数来拟合。

        ​

        显然直线无论怎么拟合的效果都不是特别的好，如果引入平方项

                        

​

        看起来拟合的效果更好了一点，但是由于二次函数模型是个抛物线最终会降下来，那么就意味着随着房子面积的不断增加达到一个临界点之后，房子面积还继续增加，但是此时的房子价格却不会继续上升，而是开始下降，这是不太合理的。

        如果再引入立方项，看起来就合理了一点

        

​

2.2 如何产生多项式特征

        

        现在是一个只有一次项的线性回归模型，

1.第一种方法是我们可以让其自身升幂后再加入原模型,以引入三次方为例

                令，，

        于是我们就得到了一个带有三次方的多项式回归模型

                 

2.第二种方法是自身开根，以引入开二次方为例

                令，

        于是我们就得到了一个带有二次根式的多项式回归模型

                

        该函数的曲线是如下图的趋势上升但上升到一定程度之后便慢慢变得平缓

​

        如果初始模型具有多个特征，scikit-learn构造最高次为2次的多项式，（1为偏置项对应的x）

2.3 注意使用特征缩放

        如果像上述那样设置特征 x1=(size)、x2=(size)^2、x3=(size)^3的话
        特征x1=(size)：房子面积范围大小在1到1000之间
        特征x2=(size)^2：房子面积的平方的范围大小就在1到一百万(1000的平方)之间
        特征x3=(size)^3：房子面积的平方的范围大小就在1到10的9次方之间
        可以看出上述3个特征的范围相差很大，因此如果此时使用梯度下降法的话，那么运用特征缩放就显得更加尤为重要了，因为这样才能控制值的范围变得具有可比性。

2.4 分段多项式——样条函数（Spline functions）

        在普通多项式回归中，我们通过在现有特征基础上使用多项式函数来生成新特征，对于数据集而言，这些特征具有全局性影响,随着次方的提高，会容易产生过拟合的问题。

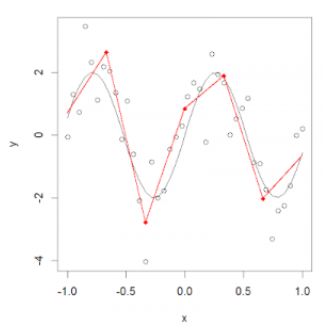
        为了解决这个问题，我们可以把数据划分成多个连续的区间，然后针对每一部分拟合线性函数或非线性的低阶多项式函数。

                                

        我们把这些分区的红点称为节点（knot），把拟合单个区间数据分布的函数称为分段函数（piecewise function）。如上图所示，这个数据分布可以用多个分段函数来拟合。

3.多项式回归的实例

        ex1data1.txt数据集包含 47 个数据样本，每个数据有三列，第一列和第二列分别是房屋大小和卧室数量的特征,最后一列是目标价格。

1.读取数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#读取数据集
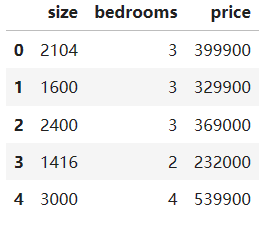
data = pd.read_csv('ex1data2.txt', delimiter=',',names = ['size','bedrooms','price'])
data.head()

2.数据预处理

# 标准化
def nomalize(data):
    return (data-data.mean())/data.std()
data = nomalize(data)
data.head()

# 构造最高次方为2的多项式特征
data.insert(0,'ones',1) 
data.insert(3,'(size)^2',data.iloc[:,1]**2)
data.insert(4,'size*bedrooms',data.iloc[:,1]*data.iloc[:,2])
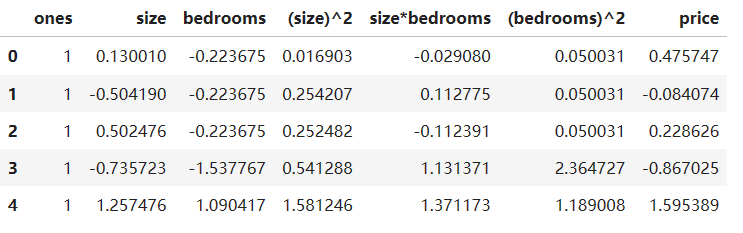
data.insert(5,'(bedrooms)^2',data.iloc[:,2]**2)
data.head()

        也可以使用sklearn，效果和上面是一样的

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)

X = data.iloc[:,0:-1] 
y = data.iloc[:,-1]
X = X.values
y = y.values
y.reshape(47,1)

3. 模型训练   

        后面的步骤和多元线性回归是一样的，手动实现多元线性回归训练在Linear regression 线性回归与梯度下降-CSDN博客，这里直接使用sklearn的相关库

from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=False) # 在数据处理已经添加了全1列,这里就不用截距了
model.fit(X, y)
print("Model Coefficients:", model.coef_)

参数

1.fit_intercept: bool, default=True。是否需要截距，就是偏置

2.positive：bool, default=False。强制系数是正的

3.copy_X：bool,optional,default True。默认为True, 否则传入的X会被改写。
4.n_jobs：int,optional,default 1int。默认为1.线程数

属性：
1.coef_：array,shape(n_features, ) or (n_targets, n_features)。回归系数(斜率)。
2.intercept_: 截距

方法

1.fit(X,y,sample_weight=None)
X:array, 稀疏矩阵 [n_samples,n_features] 
y:array [n_samples, n_targets] 
sample_weight:array [n_samples]，每条测试数据的权重，同样以矩阵方式传入
2.predict(x):预测方法，将返回值y_pred
3.get_params(deep=True)： 返回对regressor 的设置值
4.score(X,y,sample_weight=None)：评分函数，将返回一个小于1的得分，可能会小于0