计算机视觉（八）：CNN架构

计算机视觉笔记总目录

---

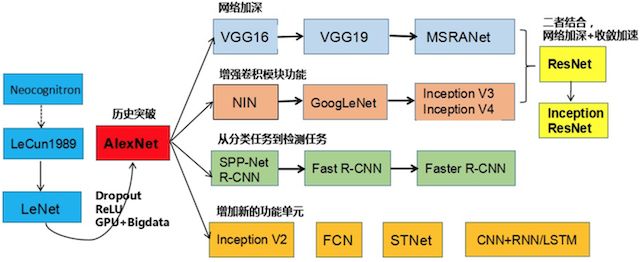
下面我们主要以一些常见的网络结构去解析，并介绍大部分的网络的特点。这里看一下卷积的发展历史图。

1 LeNet-5解析

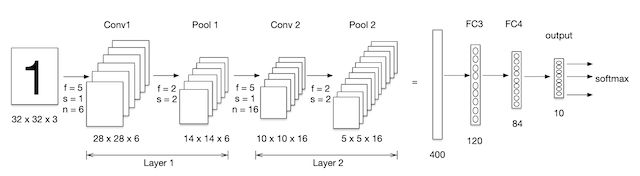
首先我们从一个稍微早一些的卷积网络结构LeNet-5，开始的目的是用来识别数字的。从前往后介绍完整的结构组成，并计算相关输入和输出。

1.1 网络结构

• 激活层默认不画网络图当中，这个网络结构当时使用的是sigmoid和Tanh函数，还没有出现Relu函数
• 将卷积、激活、池化视作一层，即使池化没有参数

1.2 参数形状总结

	shape	size	parameters
Input	(32,32,3)	3072	0
Conv1(f=5,s=1)	(28,28,6)	4704	450+6
Pool1	(14,14,6)	1176	0
Conv2(f=5,s=1)	(10,10,16)	1600	2400+16
Pool2	(5,5,16)	400	0
FC3	(120,1)	120	48000+120
FC4	(84,1)	84	10080+84
Ouput:softmax	(10,1)	10	840+10

• 中间的特征大小变化不宜过快

事实上，在过去很多年，许多机构或者学者都发布了各种各样的网络，其实去了解设计网络最好的办法就是去研究现有的网络结构或者论文。大多数网络设计出来是为了Image Net的比赛（解决ImageNet中的1000类图像分类或定位问题），后来大家在各个业务上进行使用。

2 AlexNet

2012年，Alex Krizhevsky、Ilya Sutskever在多伦多大学Geoff Hinton的实验室设计出了一个深层的卷积神经网络AlexNet，夺得了2012年ImageNet LSVRC的冠军，且准确率远超第二名（top5错误率为15.3%，第二名为26.2%），引起了很大的轰动。AlexNet可以说是具有历史意义的一个网络结构。

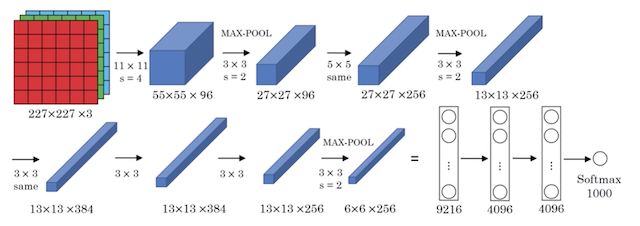
• 总参数量：60M=6000万，5层卷积+3层全连接
• 使用了非线性激活函数：ReLU
• 防止过拟合的方法：Dropout，数据扩充（Data augmentation）
• 批标准化层的使用

3 卷积网络结构的优化

3.1 常见结构特点

整个过程：AlexNet $\to$ NIN $\to$ (VGG—GoogLeNet) $\to$ ResNet $\to$ DenseNet

• NIN:引入$1\ast 1$卷积
• VGG，斩获2014年分类第二（第一是GoogLeNet），定位任务第一。
  • 参数量巨大,140M = 1.4亿
  • 19layers
  • VGG 版本
    • VGG16
    • VGG19

• GoogleNet，2014年比赛冠军的model，这个model证明了一件事：用更多的卷积，更深的层次可以得到更好的结构。（当然，它并没有证明浅的层次不能达到这样的效果）
  • 500万的参数量
  • 22layers
  • 引入了Inception模块
    • Inception V1
    • Inception V2
    • Inception V3
    • Inception V4

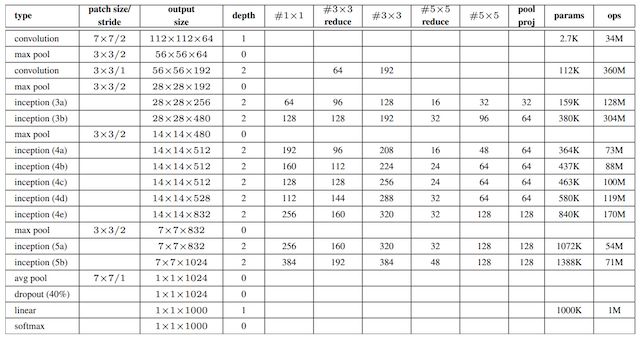
下面我们将针对卷积网络架构常用的一些结构进行详细分析，来探究这些结构带来的好处

4 VGG

特点：

• 1、VGG-16的结构非常整洁，深度较AlexNet深得多，里面包含多个conv->conv->max_pool这类的结构,VGG的卷积层都是same的卷积，即卷积过后的输出图像的尺寸与输入是一致的，它的下采样完全是由max pooling来实现。
• 2、VGG网络后接3个全连接层，filter的个数（卷积后的输出通道数）从64开始，然后没接一个pooling后其成倍的增加，128、512，注意VGG是使用小尺寸的filter，及有规则的卷积-池化操作。

闪光点：

• 卷积层使用更小的filter尺寸和间隔
• 与AlexNet相比，可以看出VGG-Nets的卷积核尺寸还是很小的，比如AlexNet第一层的卷积层用到的卷积核尺寸就是$11\ast 11$，这是一个很大卷积核了。而反观VGG-Nets，用到的卷积核的尺寸无非都是1×1和3×3的小卷积核，可以替代大的filter尺寸。

3×3卷积核的优点：

• 多个3×3的卷积层比一个大尺寸filter卷积层有更多的非线性，使得判决函数更加具有判决性
• 多个3×3的卷积层比一个大尺寸的filter有更少的参数，假设卷积层的输入和输出的特征图大小相同为C，那么三个3×3的卷积层参数个数3×（3×3×C×C）=27CC；一个7×7的卷积层参数为49CC；所以可以把三个3×3的filter看成是一个7×7filter的分解（中间层有非线性的分解）

VGG-16的Keras实现(这里只做展示了解)：

def VGG_16():   
    model = Sequential()

    model.add(Conv2D(64,(3,3),strides=(1,1),input_shape=(224,224,3),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(64,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(MaxPooling2D(pool_size=(2,2)))

    model.add(Conv2D(128,(3,2),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(128,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(MaxPooling2D(pool_size=(2,2)))

    model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(MaxPooling2D(pool_size=(2,2)))

    model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(MaxPooling2D(pool_size=(2,2)))

    model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(MaxPooling2D(pool_size=(2,2)))

    model.add(Flatten())
    model.add(Dense(4096,activation='relu'))
    model.add(Dropout(0.5))
    model.add(Dense(4096,activation='relu'))
    model.add(Dropout(0.5))
    model.add(Dense(1000,activation='softmax'))

    return model

5 Inception 结构

首先我们要说一下在Network in Network中引入的1 x 1卷积结构的相关作用，下面我们来看$1\ast 1$卷积核的优点

5.1 MLP卷积（1 x 1卷积）

目的： 提出了一种新的深度网络结构，称为“网络中的网络”（NIN），增强接受域内局部贴片的模型判别能力。

做法：

• 对于传统线性卷积核：采用线性滤波器，然后采用非线性激活。
• 提出MLP卷积取代传统线性卷积核

作用或优点：

• 1x1的卷积核操作可以实现卷积核通道数的降维和升维，实现参数的减小化

5.2 卷积介绍（1 x 1卷积）

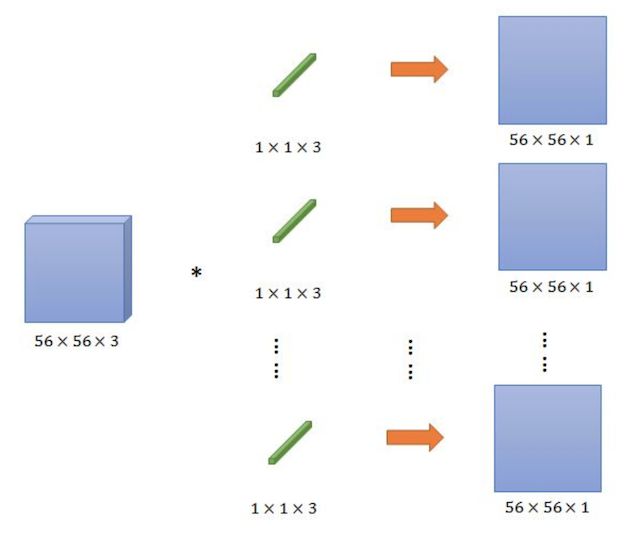
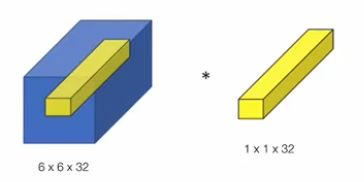
从图中，看到1 x 1卷积的过程，那么这里先假设只有3个1x1Filter，那么最终结果还是56x56x3。但是每一个FIlter的三个参数的作用

• 看作是对三个通道进行了线性组合。

我们甚至可以把这几个FIlter可以看成就是一个简单的神经元结构，每个神经元参数数量与前面的通道数量相等。

• 通常在卷积之后会加入非线性激活函数，在这里之后加入激活函数，就可以理解成一个简单的MLP网络了。

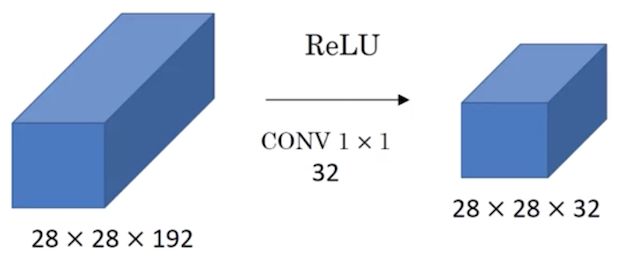
5.3 通道数变化

那么对于1x1网络对通道数的变化，其实并不是最重要的特点，因为毕竟3 x 3，5 x 5都可以带来通道数的变化

而1x1卷积的参数并不多，我们拿下面的例子来看

• 保持通道数不变
• 提升通道数
• 减少通道数

对于单通道输入，1×1的卷积确实不能起到降维作用，但对于多通道输入，就不不同了。假设你有256个特征输入，256个特征输出，同时假设Inception层只执行3×3的卷积。这意味着总共要进行 256×256×3×3的卷积（589000次乘积累加（MAC）运算）。这可能超出了我们的计算预算，比方说，在Google服务器上花0.5毫秒运行该层。

作为替代，我们决定减少需要卷积的特征的数量，比如减少到64（256/4）个。在这种情况下，我们首先进行256到64的1×1卷积，然后在所有Inception的分支上进行64次卷积，接着再使用一个64到256的1×1卷积。

• 256×64×1×1 = 16000
• 64×64×3×3 = 36000
• 64×256×1×1 = 16000

现在的计算量大约是70000(即16000+36000+16000)，相比之前的约600000，几乎减少了10倍。这就通过小卷积核实现了降维

5.4 Inception层

这个结构其实还有名字叫盗梦空间结构。

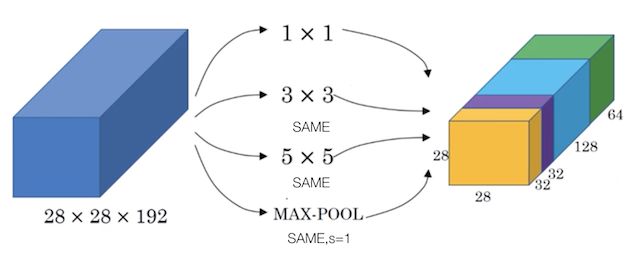
目的： 代替人手工去确定到底使用1x1,3x3,5x5还是是否需要max_pooling层，由网络自动去寻找适合的结构。并且节省计算。

特点：

• 是每一个卷积/池化最终结果的长、宽大小一致
• 特殊的池化层，需要增加padding，步长为1来使得输出大小一致，并且选择32的通道数
• 最终结果28 x 28 x 256
  • 使用更少的参数，达到跟AlexNet或者VGG同样类似的输出结果

5.5 Inception v1-Pointwise Conv