13.二进制枚举练习题
文章目录
- 二进制枚举练习题
-
- [78. 子集](https://leetcode.cn/problems/subsets/)
- [77. 组合](https://leetcode.cn/problems/combinations/)
- [1286. 字母组合迭代器](https://leetcode.cn/problems/iterator-for-combination/)
- [2397. 被列覆盖的最多行数](https://leetcode.cn/problems/maximum-rows-covered-by-columns/)
- [2212. 射箭比赛中的最大得分](https://leetcode.cn/problems/maximum-points-in-an-archery-competition/)
- [1601. 最多可达成的换楼请求数目](https://leetcode.cn/problems/maximum-number-of-achievable-transfer-requests/)
- [2959. 关闭分部的可行集合数目](https://leetcode.cn/problems/number-of-possible-sets-of-closing-branches/)
二进制枚举练习题
1、从空集枚举到全集
for (int s = 0; s < (1 << n); s++) {
// 处理 s 的逻辑
}
2、遍历集合
设元素范围从 0 到 n−1,挨个判断元素是否在集合 s 中:
for (int i = 0; i < n; i++) {
if (((s >> i) & 1) == 1) { // i 在 s 中
// 处理 i 的逻辑
}
}
题单
https://leetcode.cn/problems/number-of-possible-sets-of-closing-branches/solutions/2560722/er-jin-zhi-mei-ju-floydgao-xiao-xie-fa-f-t7ou/
-
78. 子集
-
77. 组合
-
1286. 字母组合迭代器 1591
-
2397. 被列覆盖的最多行数 1719
-
2212. 射箭比赛中的最大得分 1869
-
1601. 最多可达成的换楼请求数目 2119
-
2959. 关闭分部的可行集合数目
78. 子集
中等
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums中的所有元素 互不相同
// 位运算优化
class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
int n = nums.length;
// 从空集枚举到全集
for(int s = 0; s < (1 << n); s++){
List<Integer> tmp = new ArrayList<>();
// 遍历集合
for(int j = 0; j < n; j++){
if(((s >> j) & 1) == 1){ // j 在 s 中
tmp.add(nums[j]);
}
}
res.add(new ArrayList<>(tmp));
}
return res;
}
}
77. 组合
中等
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
提示:
1 <= n <= 201 <= k <= n
枚举所有大小为k的子集
class Solution {
public List<List<Integer>> combine(int n, int k) {
List<List<Integer>> res = new ArrayList<>();
for(int s = 0; s < (1 << n); s++){
if(Integer.bitCount(s) == k){
List<Integer> tmp = new ArrayList<>();
for(int j = 0; j < n; j++){
if(((s >> j) & 1) == 1)
tmp.add(j+1);
}
res.add(tmp);
}
}
return res;
}
}
1286. 字母组合迭代器
中等
请你设计一个迭代器类 CombinationIterator ,包括以下内容:
CombinationIterator(string characters, int combinationLength)一个构造函数,输入参数包括:用一个 有序且字符唯一 的字符串characters(该字符串只包含小写英文字母)和一个数字combinationLength。- 函数
next(),按 字典序 返回长度为combinationLength的下一个字母组合。 - 函数
hasNext(),只有存在长度为combinationLength的下一个字母组合时,才返回true
示例 1:
输入:
["CombinationIterator", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[["abc", 2], [], [], [], [], [], []]
输出:
[null, "ab", true, "ac", true, "bc", false]
解释:
CombinationIterator iterator = new CombinationIterator("abc", 2); // 创建迭代器 iterator
iterator.next(); // 返回 "ab"
iterator.hasNext(); // 返回 true
iterator.next(); // 返回 "ac"
iterator.hasNext(); // 返回 true
iterator.next(); // 返回 "bc"
iterator.hasNext(); // 返回 false
提示:
1 <= combinationLength <= characters.length <= 15characters中每个字符都 不同- 每组测试数据最多对
next和hasNext调用104次 - 题目保证每次调用函数
next时都存在下一个字母组合。
class CombinationIterator {
List<String> list;
int idx;
public CombinationIterator(String characters, int combinationLength) {
list = new ArrayList<>();
// 转为组合问题,枚举所有长度为combiantionlength的组合
int n = characters.length();
for(int s = 0; s < (1 << n); s++){
if(Integer.bitCount(s) == combinationLength){
StringBuilder sb = new StringBuilder();
for(int j = 0; j < n; j++){
if(((s >> j) & 1) == 1)
sb.append(characters.charAt(j));
}
list.add(sb.toString());
}
}
Collections.sort(list, (a, b) -> a.compareTo(b));
idx = 0;
}
public String next() {
String s = list.get(idx);
idx++;
return s;
}
public boolean hasNext() {
return idx < list.size();
}
}
使用list的迭代器
class CombinationIterator {
Iterator<String> iterator;
public CombinationIterator(String characters, int combinationLength) {
List<String> list = new ArrayList<>();
// 转为组合问题,枚举所有长度为combiantionlength的组合
int n = characters.length();
for(int s = 0; s < (1 << n); s++){
if(Integer.bitCount(s) == combinationLength){
StringBuilder sb = new StringBuilder();
for(int j = 0; j < n; j++){
if(((s >> j) & 1) == 1)
sb.append(characters.charAt(j));
}
list.add(sb.toString());
}
}
Collections.sort(list);
iterator = list.iterator();
}
public String next() {
return iterator.next();
}
public boolean hasNext() {
return iterator.hasNext();
}
}
2397. 被列覆盖的最多行数
中等
给你一个下标从 0 开始、大小为 m x n 的二进制矩阵 matrix ;另给你一个整数 numSelect,表示你必须从 matrix 中选择的 不同 列的数量。
如果一行中所有的 1 都被你选中的列所覆盖,则认为这一行被 覆盖 了。
形式上,假设 s = {c1, c2, ...., cnumSelect} 是你选择的列的集合。对于矩阵中的某一行 row ,如果满足下述条件,则认为这一行被集合 s 覆盖:
- 对于满足
matrix[row][col] == 1的每个单元格matrix[row][col](0 <= col <= n - 1),col均存在于s中,或者 row中 不存在 值为1的单元格。
你需要从矩阵中选出 numSelect 个列,使集合覆盖的行数最大化。
返回一个整数,表示可以由 numSelect 列构成的集合 覆盖 的 最大行数 。
示例 1:
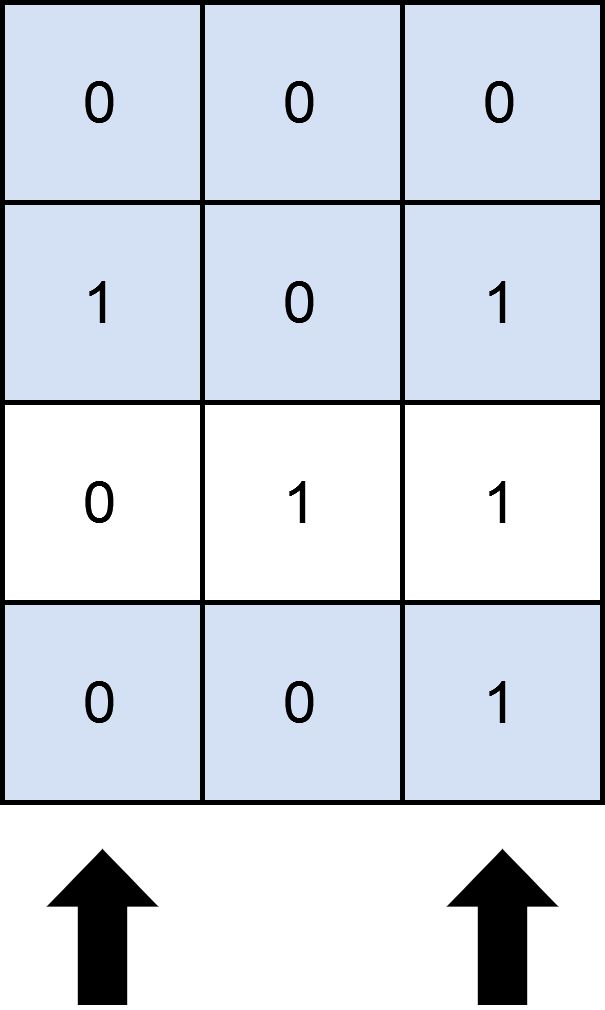
输入:matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
输出:3
解释:
图示中显示了一种覆盖 3 行的可行办法。
选择 s = {0, 2} 。
- 第 0 行被覆盖,因为其中没有出现 1 。
- 第 1 行被覆盖,因为值为 1 的两列(即 0 和 2)均存在于 s 中。
- 第 2 行未被覆盖,因为 matrix[2][1] == 1 但是 1 未存在于 s 中。
- 第 3 行被覆盖,因为 matrix[2][2] == 1 且 2 存在于 s 中。
因此,可以覆盖 3 行。
另外 s = {1, 2} 也可以覆盖 3 行,但可以证明无法覆盖更多行。
示例 2:
输入:matrix = [[1],[0]], numSelect = 1
输出:2
解释:
选择唯一的一列,两行都被覆盖了,因为整个矩阵都被覆盖了。
所以我们返回 2 。
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 12matrix[i][j]要么是0要么是11 <= numSelect <= n
class Solution {
/**
1. 将二维矩阵压缩为一维矩阵,中间的元素用位(1<
public int maximumRows(int[][] matrix, int numSelect) {
int m = matrix.length, n = matrix[0].length;
int[] rows = new int[m];
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(matrix[i][j] == 1)
rows[i] |= (1 << j);
}
}
int res = 0;
for(int s = 1; s < (1 << n); s++){
if(Integer.bitCount(s) == numSelect){
int x = 0;
for(int i = 0; i < n; i++){
if(((s >> i) & 1) == 1)
x |= (1 << i);
}
int cnt = 0;
for(int i = 0; i < m; i++){
if((rows[i] & x) == rows[i])
cnt += 1;
}
res = Math.max(res, cnt);
}
}
return res;
}
}
2212. 射箭比赛中的最大得分
中等
Alice 和 Bob 是一场射箭比赛中的对手。比赛规则如下:
- Alice 先射
numArrows支箭,然后 Bob 也射numArrows支箭。 - 分数按下述规则计算:
- 箭靶有若干整数计分区域,范围从
0到11(含0和11)。 - 箭靶上每个区域都对应一个得分
k(范围是0到11),Alice 和 Bob 分别在得分k区域射中ak和bk支箭。如果ak >= bk,那么 Alice 得k分。如果ak < bk,则 Bob 得k分 - 如果
ak == bk == 0,那么无人得到k分。
- 箭靶有若干整数计分区域,范围从
- 例如,Alice 和 Bob 都向计分为
11的区域射2支箭,那么 Alice 得11分。如果 Alice 向计分为11的区域射0支箭,但 Bob 向同一个区域射2支箭,那么 Bob 得11分。
给你整数 numArrows 和一个长度为 12 的整数数组 aliceArrows ,该数组表示 Alice 射中 0 到 11 每个计分区域的箭数量。现在,Bob 想要尽可能 最大化 他所能获得的总分。
返回数组 bobArrows ,该数组表示 Bob 射中 0 到 11 每个 计分区域的箭数量。且 bobArrows 的总和应当等于 numArrows 。
如果存在多种方法都可以使 Bob 获得最大总分,返回其中 任意一种 即可。
示例 1:
输入:numArrows = 9, aliceArrows = [1,1,0,1,0,0,2,1,0,1,2,0]
输出:[0,0,0,0,1,1,0,0,1,2,3,1]
解释:上表显示了比赛得分情况。
Bob 获得总分 4 + 5 + 8 + 9 + 10 + 11 = 47 。
可以证明 Bob 无法获得比 47 更高的分数。
示例 2:
输入:numArrows = 3, aliceArrows = [0,0,1,0,0,0,0,0,0,0,0,2]
输出:[0,0,0,0,0,0,0,0,1,1,1,0]
解释:上表显示了比赛得分情况。
Bob 获得总分 8 + 9 + 10 = 27 。
可以证明 Bob 无法获得比 27 更高的分数。
提示:
1 <= numArrows <= 105aliceArrows.length == bobArrows.length == 120 <= aliceArrows[i], bobArrows[i] <= numArrowssum(aliceArrows[i]) == numArrows
class Solution {
/**
由于只有 12 个区域,可以枚举Bob在哪些区域获胜
为了节省箭的数量,Bob在获胜区域只需要比Alice多射一支箭
如果有多余的箭未射出,则累加到任意一个区域上
*/
public int[] maximumBobPoints(int numArrows, int[] aliceArrows) {
int n = aliceArrows.length;
int[] res = new int[n];
int maxScore = 0;
for(int s = 0; s < (1 << n); s++){
int score = 0;
int usedArrows = 0;
int[] bobArrows = new int[n];
for(int j = 0; j < 12; j++){
if((s >> j & 1) == 1){
score += j;
usedArrows += aliceArrows[j] + 1;
bobArrows[j] = aliceArrows[j] + 1;
}
}
if(usedArrows > numArrows){
continue; // 需要的箭数超过最大个数
}
if(score > maxScore){
maxScore = score;
bobArrows[0] += (numArrows - usedArrows); // 没用完的箭随意放在第一个区域
res = bobArrows;
}
}
return res;
}
}
1601. 最多可达成的换楼请求数目
困难
我们有 n 栋楼,编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节,部分员工想要换一栋楼居住。
给你一个数组 requests ,其中 requests[i] = [fromi, toi] ,表示一个员工请求从编号为 fromi 的楼搬到编号为 toi 的楼。
一开始 所有楼都是满的,所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0 。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 n = 3 且两个员工要离开楼 0 ,一个员工要离开楼 1 ,一个员工要离开楼 2 ,如果该请求列表可行,应该要有两个员工搬入楼 0 ,一个员工搬入楼 1 ,一个员工搬入楼 2 。
请你从原请求列表中选出若干个请求,使得它们是一个可行的请求列表,并返回所有可行列表中最大请求数目。
示例 1:
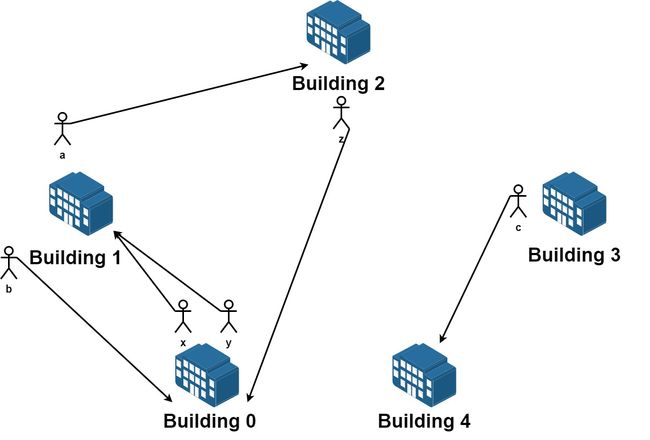
输入:n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
输出:5
解释:请求列表如下:
从楼 0 离开的员工为 x 和 y ,且他们都想要搬到楼 1 。
从楼 1 离开的员工为 a 和 b ,且他们分别想要搬到楼 2 和 0 。
从楼 2 离开的员工为 z ,且他想要搬到楼 0 。
从楼 3 离开的员工为 c ,且他想要搬到楼 4 。
没有员工从楼 4 离开。
我们可以让 x 和 b 交换他们的楼,以满足他们的请求。
我们可以让 y,a 和 z 三人在三栋楼间交换位置,满足他们的要求。
所以最多可以满足 5 个请求。
示例 2:
输入:n = 3, requests = [[0,0],[1,2],[2,1]]
输出:3
解释:请求列表如下:
从楼 0 离开的员工为 x ,且他想要回到原来的楼 0 。
从楼 1 离开的员工为 y ,且他想要搬到楼 2 。
从楼 2 离开的员工为 z ,且他想要搬到楼 1 。
我们可以满足所有的请求。
示例 3:
输入:n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
输出:4
提示:
1 <= n <= 201 <= requests.length <= 16requests[i].length == 20 <= fromi, toi < n
class Solution {
/**
1 <= requests.length <= 16
1 <= n <= 20
枚举可以满足的请求列表
*/
public int maximumRequests(int n, int[][] requests) {
int m = requests.length;
int maxRequest = 0;
for(int s = 1; s < (1 << m); s++){
int[] cnt = new int[n]; // 变化数组
for(int j = 0; j < m; j++){
if((s >> j & 1) == 1){
int from = requests[j][0], to = requests[j][1];
cnt[from] -= 1;
cnt[to] += 1;
}
}
boolean available = true;
for(int i = 0; i < n; i++){
if(cnt[i] != 0){
available = false;
break;
}
}
if(available){
maxRequest = Math.max(maxRequest, Integer.bitCount(s));
}
}
return maxRequest;
}
}
2959. 关闭分部的可行集合数目
困难
一个公司在全国有 n 个分部,它们之间有的有道路连接。一开始,所有分部通过这些道路两两之间互相可以到达。
公司意识到在分部之间旅行花费了太多时间,所以它们决定关闭一些分部(也可能不关闭任何分部),同时保证剩下的分部之间两两互相可以到达且最远距离不超过 maxDistance 。
两个分部之间的 距离 是通过道路长度之和的 最小值 。
给你整数 n ,maxDistance 和下标从 0 开始的二维整数数组 roads ,其中 roads[i] = [ui, vi, wi] 表示一条从 ui 到 vi 长度为 wi的 无向 道路。
请你返回关闭分部的可行方案数目,满足每个方案里剩余分部之间的最远距离不超过 maxDistance。
注意,关闭一个分部后,与之相连的所有道路不可通行。
注意,两个分部之间可能会有多条道路。
示例 1:
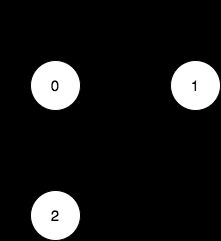
输入:n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]]
输出:5
解释:可行的关闭分部方案有:
- 关闭分部集合 [2] ,剩余分部为 [0,1] ,它们之间的距离为 2 。
- 关闭分部集合 [0,1] ,剩余分部为 [2] 。
- 关闭分部集合 [1,2] ,剩余分部为 [0] 。
- 关闭分部集合 [0,2] ,剩余分部为 [1] 。
- 关闭分部集合 [0,1,2] ,关闭后没有剩余分部。
总共有 5 种可行的关闭方案。
示例 2:
输入:n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]]
输出:7
解释:可行的关闭分部方案有:
- 关闭分部集合 [] ,剩余分部为 [0,1,2] ,它们之间的最远距离为 4 。
- 关闭分部集合 [0] ,剩余分部为 [1,2] ,它们之间的距离为 2 。
- 关闭分部集合 [1] ,剩余分部为 [0,2] ,它们之间的距离为 2 。
- 关闭分部集合 [0,1] ,剩余分部为 [2] 。
- 关闭分部集合 [1,2] ,剩余分部为 [0] 。
- 关闭分部集合 [0,2] ,剩余分部为 [1] 。
- 关闭分部集合 [0,1,2] ,关闭后没有剩余分部。
总共有 7 种可行的关闭方案。
示例 3:
输入:n = 1, maxDistance = 10, roads = []
输出:2
解释:可行的关闭分部方案有:
- 关闭分部集合 [] ,剩余分部为 [0] 。
- 关闭分部集合 [0] ,关闭后没有剩余分部。
总共有 2 种可行的关闭方案。
提示:
1 <= n <= 101 <= maxDistance <= 1050 <= roads.length <= 1000roads[i].length == 30 <= ui, vi <= n - 1ui != vi1 <= wi <= 1000- 一开始所有分部之间通过道路互相可以到达。
class Solution {
/**
0 <= roads.length <= 1000
枚举保留哪些节点,在这些节点之间连边
然后用Floyd算法求出任意两点之间的最短路,
若保留节点之间的最短路均不超过maxDistance,记录答案
*/
public int numberOfSets(int n, int maxDistance, int[][] roads) {
// 预处理原图的邻接矩阵g
int[][] g = new int[n][n];
for(int i = 0; i < n; i++){
Arrays.fill(g[i], Integer.MAX_VALUE / 2); // 加法防溢出
g[i][i] = 0;
}
for(int[] e : roads){
int x = e[0], y = e[1], wt = e[2];
g[x][y] = Math.min(g[x][y], wt);
g[y][x] = Math.min(g[y][x], wt);
}
int res = 0;
int[][] f = new int[n][n];
next:
//遍历所有方案数,当前方案i的二进制中为1的位置则表示该节点没有被删除,为0则表示被删除
for(int s = 0; s < (1 << n); s++){
for(int i = 0; i < n; i++){
if(((s >> i) & 1) == 1){
System.arraycopy(g[i], 0, f[i], 0, n);
}
}
// Floyd
for (int k = 0; k < n; k++) {
if ((s >> k & 1) == 0) continue;
for (int i = 0; i < n; i++) {
if ((s >> i & 1) == 0) continue;
for (int j = 0; j < n; j++) {
f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j]);
}
}
}
for (int i = 0; i < n; i++) {
if ((s >> i & 1) == 0) continue;
for (int j = 0; j < n; j++) {
if ((s >> j & 1) == 1 && f[i][j] > maxDistance) {
continue next;
}
}
}
res++;
}
return res;
}
}