数据结构--迪杰斯特拉（Dijkstra）算法

生活封锁了我们，只要我们的心不死，生活便永远不是一汪死水，而我们，依然会绽放最美的姿态。

什么是迪杰斯特拉算法

算法来历

戴克斯特拉算法（英语：Dijkstra’s algorithm），又称迪杰斯特拉算法、Dijkstra算法，是由荷兰计算机科学家艾兹赫尔·戴克斯特拉在1956年发现的算法，并于3年后在期刊上发表。戴克斯特拉算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题。

该算法存在很多变体：戴克斯特拉的原始版本仅适用于找到两个顶点之间的最短路径，后来更常见的变体固定了一个顶点作为源结点然后找到该顶点到图中所有其它结点的最短路径，产生一个最短路径树。

算法的用途

该算法解决了图 上带权的单源最短路径问题。具体来说，戴克斯特拉算法设置了一顶点集合S，在集合S中所有的顶点与源点s之间的最终最短路径权值均已确定。该算法常用于路由算法或者作为其他图算法的一个子模块。举例来说，如果图中的顶点表示城市，而边上的权重表示城市间开车行经的距离，该算法可以用来找到两个城市之间的最短路径。

迪杰斯特拉算法的理论

首先举出图例1，在图中选择下标为0的V0点开始遍历。

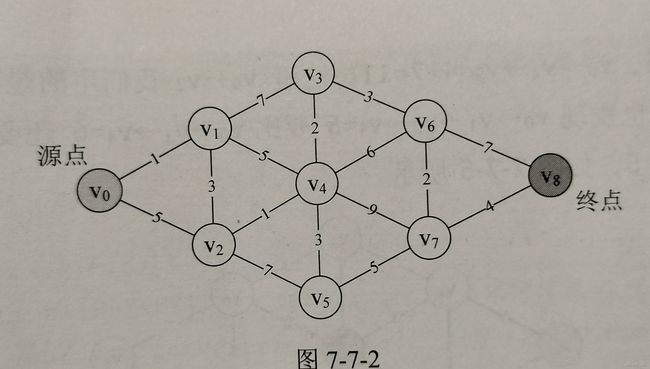
不难看出，从v0开始选择最短路径，即V0->V1，再进行选择遍历，即V0->V1->V2,如图例2所示。

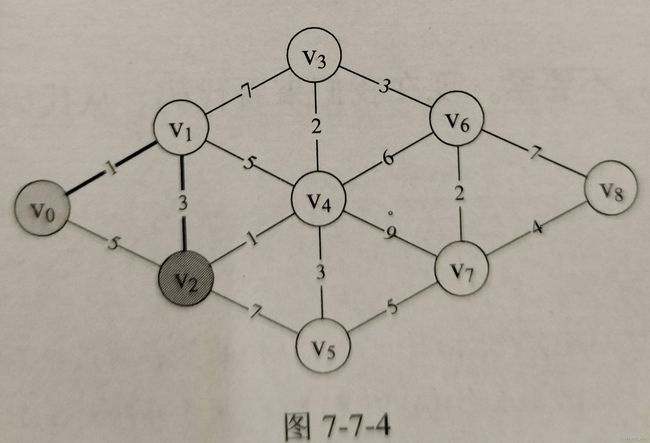
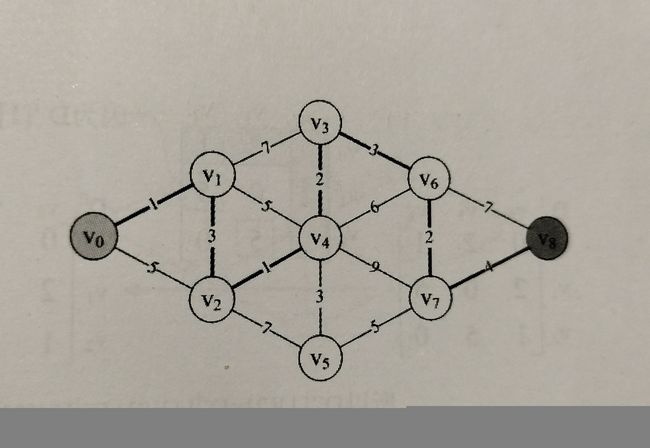
如此反复，就可以得到源点V0至终点V8的最短权值路径。如图例3所示。

迪杰斯特拉算法实现

首先，我们需要知道，迪杰斯特拉算法是基于邻接矩阵实现的，如过对于邻接矩阵还有些不熟悉的同学可以复习一下点我复习邻接矩阵
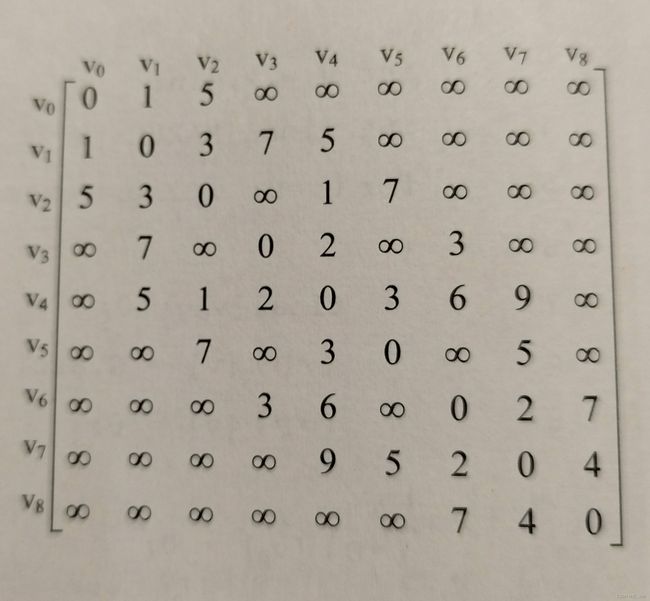
之前的图结构，转化成邻接矩阵如图例4所示。

宏定义

#include 
#include 
#define INFINITY 65535
#define MAXVEX 9
typedef int Patharc[MAXVEX];       //用于存储最短路径下标的数组
typedef int ShortPathTable[MAXVEX];//用于存储最短路径的权值和
typedef char VertexType;           //顶点类型
typedef int EdgeType;              //边上的权值

前提函数实现

typedef struct
{
	VertexType vexs[MAXVEX];//顶点表
	EdgeType arc[MAXVEX][MAXVEX];//邻接矩阵
	int numVertexes, numEdges;//顶点数以及边数
}MGraph;

void CreateMGraph(MGraph* G)
{
	int  k, w;
	char i, j;
	printf("输入顶点数和边数：\n");
	scanf("%d%d", &G->numVertexes, &G->numEdges);
	printf("请输入顶点信息：");
	getchar();
	for (i = 0; i < G->numVertexes; i++)//分别输入顶点信息
	{
		scanf("%c", &G->vexs[i]);
		getchar();
	}
	for (i = 0; i < G->numVertexes; i++)
		for (j = 0; j < G->numVertexes; j++)
			G->arc[i][j] = INFINITY;    //初始化所有点之间权无穷大

	for (k = 0; k < G->numEdges; k++)
	{
		printf("输入边(vi,vj)上的下标i，下标j和权w:\n");
		scanf("%d%d%d", &i, &j, &w);
		G->arc[i][j] = w;
		G->arc[j][i] = G->arc[i][j];//无向图，矩阵对称
	}
}

迪杰斯特拉算法

void ShortestPath_Dijkstra(MGraph G, int V0, Patharc* P, ShortPathTable* D)
{
	int v, w, k, min;
	int final[MAXVEX];   //final[w]=1表示求得顶点V0至Vw的最短路径
	for (v = 0; v < G.numVertexes; v++)
	{
		final[v] = 0;            //全部顶点初始化为未知最短路径状态
		(*D)[v] = G.arc[V0][v];  //将与V0点有连线的顶点加上权值
		(*P)[v] = 0;             //初始化路径数组P为0
	}

	(*D)[V0] = 0;                //v0至v0的路径为0
	final[V0] = 1;               //v0至v0不需要求路径

	//开始主循环，每次求得v0到某个v顶点的最短路径
	for (v = 1; v < G.numVertexes; v++)
	{
		min = INFINITY;
		for (w = 0; w < G.numVertexes; w++)
		{
			if (!final[w] && (*D)[w] < min)
			{
				k = w;
				min = (*D)[w];    //w顶点距离v0更近
			}
		}

		final[k] = 1;             //表示k下标的顶点已经在路径中
		for (w = 0; w < G.numVertexes; w++)//检查一遍
		{
			if (!final[w] && (min+G.arc[k][w]<(*D)[w]))
			{
				(*D)[w] = min + G.arc[k][w];
				(*P)[w] = k;
			}
		}
	}
}

主函数实现

int main()
{
	MGraph G;
	CreateMGraph(&G);
    Patharc P;
	ShortPathTable D;
	ShortestPath_Dijkstra(G,0,&P,&D);
}

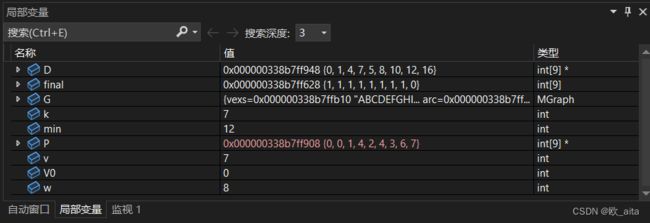
调试结果

1) D数组中每个下标的的数据对应到达此下标顶点的最短权值。

2) final数组表示数组中的各点是否进入最短路径。

3）P数组表示数组中的各点的前一个顶点

代码解析

定义一个用于存储最短路径下标的数组

typedef int Patharc[MAXVEX]; 
 Patharc P;

定义一个用于存储最短权值和的数组

typedef int ShortPathTable[MAXVEX];
ShortPathTable D;

定义一个判断一点是否进入最短路径的数组，1表示已进入，0表示未进入。

int final[MAXVEX]; 

对各项数据进行初始化，以便进行遍历。

for (v = 0; v < G.numVertexes; v++)
	{
		final[v] = 0;            //全部顶点初始化为未知最短路径状态
		(*D)[v] = G.arc[V0][v];  //将与V0点有连线的顶点加上权值
		(*P)[v] = 0;             //初始化路径数组P为0
	}
	(*D)[V0] = 0;                //v0至v0的路径为0
	final[V0] = 1;               //v0至v0不需要求路径

进行第一遍遍历，注意这里的（*D）[]是之前初始化的第一行数组数据。

		min = INFINITY;
		for (w = 0; w < G.numVertexes; w++)
		{
			if (!final[w] && (*D)[w] < min)
			{
				k = w;
				min = (*D)[w];    //w顶点距离v0更近
			}
		}

		final[k] = 1;             //表示k下标的顶点已经在路径中

这可以进行第一遍遍历，但是再往下走就不可以了，所以有了下列代码补全。

for (w = 0; w < G.numVertexes; w++)//检查一遍
		{
			if (!final[w] && (min+G.arc[k][w]<(*D)[w]))
			{
				(*D)[w] = min + G.arc[k][w];
				(*P)[w] = k;
			}
		}