C语言【数据在内存中的存储】~

一.引言

   我们知道我们的整形，浮点型这些数据是存储在内存中的，那你是否好奇他在内存中存储的，跟博主一起来增长增长内功吧~   ^-^

二.整形在内存中的存储

  原码 反码 补码

1.整数的二进制表示有三种：原码，反码，补码。

对于signed int : 最高位是符号位（1负，0正），其他都是数值位

对于unsigned int : 全部都是数值位  （这也是为什么unsigned最高取值比signed高的原因）

在内存中存的是补码，而在打印时用的是原码。

2.原码 反码 补码 的转化

对于正整数（unsigned int)他们的原码反码补码相同

对于负整数我们需要一点变化：

前面我们说到内存存的是补码，为什么呢？

    使⽤补码,可以将符号位和数值域统⼀处理； 同时加法和减法也可以统⼀处理（CPU只有加法器）此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

大小端字节序

#include 
int main()
{
 int a = 0x11223344;
 
 return 0;
}

我们在调试发现低位字节44是放在前面的也就是低地址，高位字节11是放在后面也就是高地址

这种字节存储顺序就叫做小端存储。而相对的高字节放在低地址，低位字节放在高地址就是大端存储。

为什么会有大小端之分？

这是因为在计算机系统中，我们是以字节为单位的，每个地址单元都对应着⼀个字节，⼀个字节为8 bit 位，但是在C语⾔中除了8 bit 的 char 之外，还有16 bit 的 short 型，32 bit 的 long 型（要看

具体的编译器），另外，对于位数⼤于8位的处理器，例如16位或者32位的处理器，由于寄存器宽度⼤于⼀个字节，那么必然存在着⼀个 如何将多个字节安排 的问题。因此就导致了⼤端存储模式和⼩端存储模式。（大小端灵感来源于格列佛游记）

小科普:  我们常⽤的 X86 结构是⼩端模式，⽽KEIL C51 则为⼤端模式。很多的ARM，DSP都为⼩端模式。有些ARM处理器还可以由硬件来选择是⼤端模式还是⼩端模式。

关于unsigned和signed char

1.取值范围 

你是否好奇为什么signed char 和unsigned char 的取值范围分别是-128~127和0~255呢？

我们知道char是1个字节，二进制就是8个bit位，结合之前的知识我们可以不断加1得到他们数值变化

我们可以明显看到无符号和有符号的差异，值得注意的是有符号的10000000规定是-128，他们就像一个不断循环的圆环，注意对于有符号127+1是-128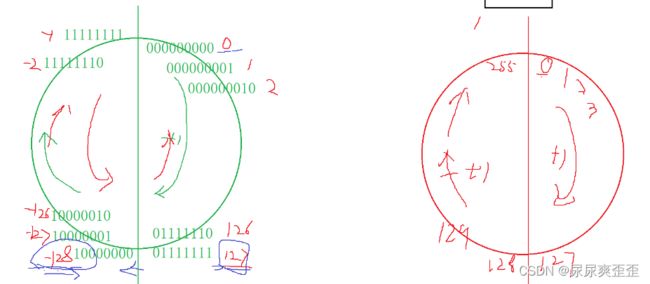

char类型截断：当一个整形32位存进char会发生截断只存进8位，当打印时会发生整形提升，有符号的补符号位，无符号的补0.

说完了整形在内存的存储，我们要说个大家伙，浮点型在内存中的存储。

三.浮点型在内存中的存储

浮点型的存储

根据国际标准IEEE（电⽓和电⼦⼯程协会） 754，任意⼀个⼆进制浮点数V可以表⽰成下⾯的形式：

V   =  (−1) ^S ∗ M ∗ 2^ E  (^表示指数)

• (−1) S 表⽰符号位，当S=0，V为正数；当S=1，V为负数

• M 表⽰有效数字，M是⼤于等于1，⼩于2的

•   E 表⽰指数位

注意：有些浮点数是不能精确保存的。

 

example：

⼗进制的5.0，写成⼆进制是 101.0 ，相当于 1.01×2^2 。

那么，按照上⾯V的格式，可以得出S=0，M=1.01，E=2。

⼗进制的-5.0，写成⼆进制是 -101.0 ，相当于 -1.01×2^2 。那么，S=1，M=1.01，E=2。

IEEE 754规定：

对于 32 位的浮点数，最⾼的1位存储符号位S，接着的 8 位存储指数E，剩下的 23 位存储有效数字M

对于 64 位的浮点数，最⾼的1位存储符号位S，接着的 11 位存储指数E，剩下的 52 位存储有效数字M

M : 由于M是大于等于1，小于2，所以为了节省空间，我们 小数点前的1 是不存进去的，只在读取时加上. ⽐如保存1.01的时候，只保存01，等到读取的时候，再把第⼀位的1加上去。这样做的⽬

的，是节省1位有效数字。以32位浮点数为例，留给M只有23位，将第⼀位的1舍去以后，等于可以保存24位有效数字。

E   : 

⾸先，E为⼀个⽆符号整数（unsigned int）

这意味着，如果E为8位，它的取值范围为0~255；如果E为11位，它的取值范围为0~2047。但是，我们知道，科学计数法中的E是可以 出现负数 的，所以IEEE 754规定，存⼊内存时E的真实值必须再加上 ⼀个中间数，对于8位的E，这个中间数是 127 ；对于11位的E，这个中间数是 1023 。⽐如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001。

浮点数的取出

浮点数的取出按照E的不同分为以下三种情况：

 E不全为0或不全为1

这时，浮点数就采⽤下⾯的规则表⽰，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第⼀位的1。

⽐如：0.5 的⼆进制形式为0.1，由于规定正数部分必须为1，即将⼩数点右移1位，则为1.0*2^(-1)，其阶码为-1+127(中间值)=126，表⽰为01111110，⽽尾数1.0去掉整数部分为0，补⻬0到23位00000000000000000000000，则其⼆进制表⽰形式为:  

0 01111110 00000000000000000000000

 E全为0

这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，有效数字M不再加上第⼀位的1，⽽是还原为0.xxxxxx的⼩数。这样做是为了表⽰±0，以及接近于0的很小的数字

    E全为1

这时，如果有效数字M全为0，表⽰±⽆穷⼤（正负取决于符号位s）；

example：

int main()
{
	int n = 9; 

	float* pFloat = (float*)&n;
	printf("n的值为：%d\n", n);//9
	//00000000 00000000 00000000 00001001
	printf("*pFloat的值为：%f\n", *pFloat);
	//浮点数在内存中的取出  0 00000000 00000000000000000001001
	//S=0 E = -126  M=0.00000000000000000001001
	*pFloat = 9.0;//浮点型在数据的存储
	//10进制 9.0
    //    1001.0
	//1.001x2^3
	//S = 0  E = 3  M = .001
	//0 00000011 00100000000000000000000
	printf("num的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);
	return 0;
}

你学会了吗？本次分享结束，希望小伙伴们多多三连！