解析FJSP问题的标准测试数据集的Python代码

---

背景问题

柔性作业车间问题（Flexible Job Shop Problem，FJSP）是经典作业车间调度问题的扩展，它允许工件的加工工序由给定的多台机器集合中的任意机器处理。柔性作业车间调度问题也是智能制造领域中的重要问题，如何高效地求解此类问题在实际生产制造中具有极其重要的理论和应用价值。

FJSP解决的是如何把若干工件的加工工序分配给产能有限的机器，并对机器上的工序进行排序，在满足工件工序的前后关系下，使完成所有工序的时间（makespan）最小。这是典型的NP-Hard问题，待加工的工序越多，工序可选设备越多（柔性越大）情况下，可选方案的数量指数级增长。

过去学术界业界对这类经典组合优化问题（FJSP）的研究非常多，进而沉淀出大量的具有标准格式的测试数据。

FJSP测试数据集介绍

数据集下载地址：https://people.idsia.ch/~monaldo/fjsp.html

在FJSP标准测试数据集中，有四个经典的数据集：

1. Barnes 数据集：包含21个算例。来源文献：B. Chambers and J. W. Barnes. Flexible Job Shop Scheduling by Tabu Search. The University of Texas, Austin, TX, Technical Report Series ORP96-09, Graduate Program in Operations Research and Industrial Engineering, 1996.
2. Brandimarte 数据集：包含10个算例。来源文献：P. Brandimarte. Routing and Scheduling in a Flexible Job Shop by Tabu Search. Annals of Operations Research, 41(3):157–183, 1993.
3. Dauzere 数据集：包含18个算例。来源文献：S. Dauzère-Pérès and J. Paulli. Solving the General Multiprocessor Job-Shop Scheduling Problem. Technical report, Rotterdam School of Management, Erasmus Universiteit Rotterdam, 1994.
4. Hurink 数据集：内部包含4个子数据集（edata/rdata/sdata/vdata），每个子数据集分别包含66个算例，这些子数据集由JSP标准测试数据集修改而来（ABZ/FT/LA/ORB）。来源文献：Hurink, B. Jurisch, and M. Thole, “Tabu search for the job-shop scheduling problem with multi-purpose machines,” Operations-Research-Spektrum, vol. 15, no. 4, pp. 205–215, 1994. 其中，sdata算例中每个工序只能分配一台机器；edata算例中有少量工序可以分配给多台机器；rdata算例中许多工序都可以分配给多台机器；vdata算例中每个工序都可以分配给多台机器。

解析FJSP标准测试数据集

测试数据文件的后缀为.fjs，以 Brandimarte 子数据集下的 MK01.fjs 为例，用记事本打开后的数据格式如下：

10	6	2
 6  2 1 5 3 4 3 5 3 3 5 2 1 2 3 4 6 2 3 6 5 2 6 1 1 1 3 1 3 6 6 3 6 4 3  
 5  1 2 6 1 3 1 1 1 2 2 2 6 4 6 3 6 5 2 6 1 1 
 5  1 2 6 2 3 4 6 2 3 6 5 2 6 1 1 3 3 4 2 6 6 6 2 1 1 5 5 
 5  3 6 5 2 6 1 1 1 2 6 1 3 1 3 5 3 3 5 2 1 2 3 4 6 2
 6  3 5 3 3 5 2 1 3 6 5 2 6 1 1 1 2 6 2 1 5 3 4 2 2 6 4 6 3 3 4 2 6 6 6
 6  2 3 4 6 2 1 1 2 3 3 4 2 6 6 6 1 2 6 3 6 5 2 6 1 1 2 1 3 4 2
 5  1 6 1 2 1 3 4 2 3 3 4 2 6 6 6 3 2 6 5 1 1 6 1 3 1
 5  2 3 4 6 2 3 3 4 2 6 6 6 3 6 5 2 6 1 1 1 2 6 2 2 6 4 6
 6  1 6 1 2 1 1 5 5 3 6 6 3 6 4 3 1 1 2 3 3 4 2 6 6 6 2 2 6 4 6
 6  2 3 4 6 2 3 3 4 2 6 6 6 3 5 3 3 5 2 1 1 6 1 2 2 6 4 6 2 1 3 4 2 

FJSP数据说明

在下载的数据包中，有个文件 DataSetExplanation.txt 是对数据如何解析进行介绍。

（1）数据首行

首先是数据的首行，包括了至少2个数字，第1个数字是工件数量，第2个数机器数量，第3个数并不一定有，表示所有工件的工序的平均可上机器数，它代表了JSP问题的柔性，柔性越大，问题的复杂度越高。

例如上述的 MK01.fjs 例子，表示有10个工件，6台机器，平均每个工序的可上机器数是2（当这个数为1时，则问题转为JSP问题）。

（2）工艺路线数据

从第2行数据开始，每一行数据均代表一个工件的工艺路线数据，从上往下依次代表工件 0、1、2…

工艺路线数据中，按顺序解析：

• 第1个数字代表该工件的工序数，例如上述数据的第2行，行首数字为6，表示该工件有6道工序；
• 接着的数据结构为 n a1 b1 a2 b2 ...an bn。n 表示工件的该工序可上的机器数，a1 表示该工序可上的机器1，b1表示该工序上机器1的加工时长。例如， 上述数据的第2行的第2个数开始为 2 1 5 3 4 3 5 3 3 5 2 1 2 3 4 6 2 3 6 5 2 6 1 1 1 3 1 3 6 6 3 6 4 3 ，解析如下：

2 1 5 3 4 3 5 3 3 5 2 1 2 3 4 6 2 3 6 5 2 6 1 1 1 3 1 3 6 6 3 6 4 3

第1步骤，可上两台设备，因此看其之后的 2*2=4 个数（或者说看其之后的2个二元数组），即2 1 5 3 4，即第一个工件的第一道工序，上机器1的加工时间为5，上机器3的加工时间为4；下一道工序的可上机器数为3，因此看后6个数，依此类推。

提取关键数据的Python代码

按行录入FJSP标准测试数据，并从中取出以下常用的模型数据：

1. 当一行数据小于等于3时（加工数据行至少4个数），说明是首行，因此取出工件数Job_num、机器数Machine_num、工序平均可选机器数average_avail_machines；
2. 反之，则为加工数据行。此时先取出数据行首元素（工件的步骤数 job_2_step_num），根据下一个数依次判断步骤的可上机器 job_step_2_avail_machines 及加工时长 job_step_machine_2_ptime，然后把相应步骤添加到机器的可加工步骤列表machine_2_avail_steps。

from collections import defaultdict

# 指定文件路径
file_path = 'Barnes/Text/mt10c1.fjs'

with open(file_path, "r", encoding='utf-8') as file:
    lines = file.readlines()

Job_num = 0         # 0,1,2...
Machine_num = 0     # 1,2,3...
average_avail_machines = 0

job_2_step_num = {}
machine_2_avail_steps = defaultdict(list)
job_step_2_avail_machines = defaultdict(list)
job_step_machine_2_ptime = {}

cur_job = -1        # 记录当前的 job 编号
for line in lines:
    line_str = line.strip().split()
    line_list = []
    for ele in line_str:
        line_list.append(int(ele))
    if len(line_list) <= 3:
        Job_num = line_list[0]
        Machine_num = line_list[1]
        average_avail_machines = line_list[2]
        for i in range(Job_num):
            job_2_step_num[i] = 0
        for k in range(1, Machine_num+1):
            machine_2_avail_steps[k] = []
    else:
        cur_job += 1
        print(line_list)
        job_2_step_num[cur_job] = line_list[0]

        cur_index = 1
        for step_index in range(job_2_step_num[cur_job]):
            avai_m_num = line_list[cur_index]
            for avail_m_index in range(avai_m_num):
                avail_m = line_list[cur_index+avail_m_index*2+1]
                ptime_ = line_list[cur_index+avail_m_index*2+2]
                job_step_2_avail_machines[cur_job, step_index].append(avail_m)
                job_step_machine_2_ptime[cur_job, step_index, avail_m] = ptime_
                machine_2_avail_steps[avail_m].append((cur_job, step_index))
            cur_index += 2*avai_m_num + 1

            print("步骤信息", job_step_2_avail_machines[cur_job, step_index])

通过修改读取文件的路径，可以自动将 FJSP 的数据读取为模型相应的数据，至此可以得到模型的工件数、工件的工序数、每个工序的可上机器数、工序上不同机器的加工时间等。

测试数据之间差异

我们做个简单的展示，看一下不同数据之间差异。

对于FJSP而言，除了 .jsp 数据中的工序平均可上设备数之外，我们还应知道每个设备的可上工序数，以及可上工序数的加工时间之和。为什么选择这两个指标？由于每个工序是无最早开始加工时间，因此在优化中相当于每个工序都可以自由选择可上设备，因此可上工序数多的设备极有概率成为瓶颈设备，进而能够加速问题的收敛。

如下图展示 Barnes 数据集下的部分数据信息：

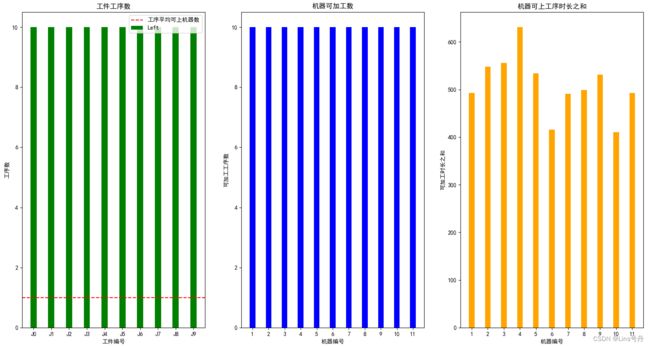
易知，Barnes 数据集每个设备的工序数一致，且机器的可加工工序数也一致，没有很明显的瓶颈机器，相同前缀的数据在图3有差异，即分布在不同机器上的可加工工序的总加工时间不一致。

画图代码

import matplotlib.pyplot as plt
import numpy as np


# 数据
machines_xtick = []
job_xtick = []
values1 = []        # 机器的可加工工序数
values2 = []        # 机器可加工工序数的时间之和
values3 = []        # 工序的可上机器数
for m in range(1, Machine_num+1):
    machines_xtick.append(f"{m}")
    values1.append(len(machine_2_avail_steps[m]))
    temp = 0
    for (i,j) in machine_2_avail_steps[m]:
        temp += job_step_machine_2_ptime[i, j, m]
    values2.append(temp)
for i in range(Job_num):
    job_xtick.append(f"J{i}")
    values3.append(job_2_step_num[i])

# 设置每个条形的宽度
bar_width = 0.35

# 创建包含两个子图的图形
fig, (ax1, ax2, ax3) = plt.subplots(1, 3)
plt.rcParams['font.sans-serif'] = ['SimHei']

# 图1
ax1.axhline(average_avail_machines, color='red', linestyle='--', label='工序平均可上机器数')
ax1.bar(np.arange(Job_num), values3, width=bar_width, label='工序数', color='green')
ax1.set_title('工件工序数')
ax1.set_xlabel('工件编号')
ax1.set_ylabel('工序数')
ax1.set_xticks(np.arange(Job_num))
ax1.set_xticklabels(job_xtick)
ax1.legend()


# 图2
ax2.bar(np.arange(Machine_num), values1, width=bar_width, color='blue')
ax2.set_title('机器可加工数')
ax2.set_xlabel('机器编号')
ax2.set_ylabel('可加工工序数')
ax2.set_xticks(np.arange(Machine_num))
ax2.set_xticklabels(machines_xtick)


# 图3
ax3.bar(np.arange(Machine_num), values2, width=bar_width, color='orange')
ax3.set_title('机器可上工序时长之和')
ax3.set_xlabel('机器编号')
ax3.set_ylabel('可加工时长之和')
ax3.set_xticks(np.arange(Machine_num))
ax3.set_xticklabels(machines_xtick)


# 调整子图之间的间距
# plt.tight_layout()

# 显示图形
plt.show()