李超线段树

李超线段树

概念

​ 李超线段树可以看作线段树的一种，与其他线段树的区别在于它维护的是平面直角坐标系内多个线段之间的关系。它的基本作用如下，

​ 给定一个平面直角坐标系，支持动态插入一条线段；当插入多个线段后，当横坐标为x时，当前所有插入线段的最值（最大值或者最小值，即当x确定时，求ymax或ymin）

实现

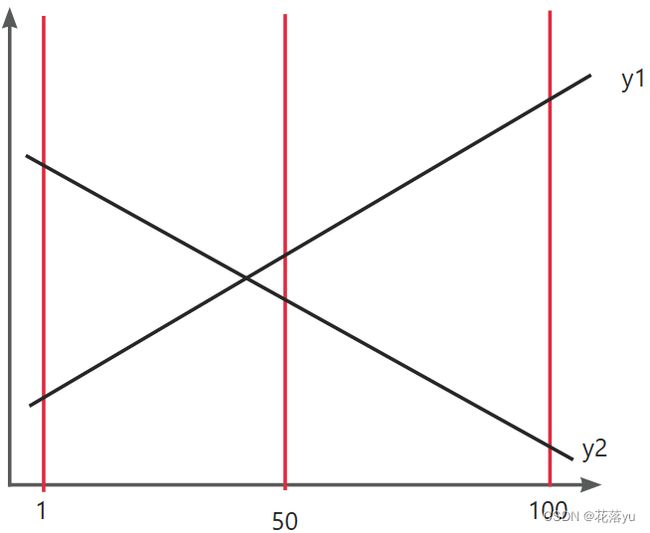
​ 李超线段树维护的每个区间，表示横坐标x的取值，它维护每个区间的“最优势线段”，即在每个区间的中点处最低的线段（以最小值为例，后面的分析都是如此），如下图所示，在区间[1,100]内，记录的是线段y2

李超线段树两个重要的操作分别是插入和查询最值

插入

往线段树里面插入一个线段，首先明确该函数传入的参数

private Node addLine(Node t, Line x, long l, long r, long xl, long xr)

其中t表示当前子树的根节点，x表示待插入的线段，l和r分别表示插入线段的横坐标的左端点和右端点，xl和xr分别表示插入线段y在左右端点处的取值，即xl=al+b，xr=ar+b，可以称为左边界和有边界。

接下来就是分情况讨论，

情况1

if (t == null)
				return new Node(x);

当根节点为空时，也就是横坐标在当前范围内并没有其它线段，那我就直接记录当前要插入的线段即可，Node(x)表示用当前线段更新根节点，然后返回。

情况2

long tl = t.x.query(l);//当前线段的左边界值
long tr = t.x.query(r);//当前线段的右边界值
if (tl <= xl && tr <= xr) {//当前线段的值全部在要插入线段的下面，则不用更新
		return t;
} 

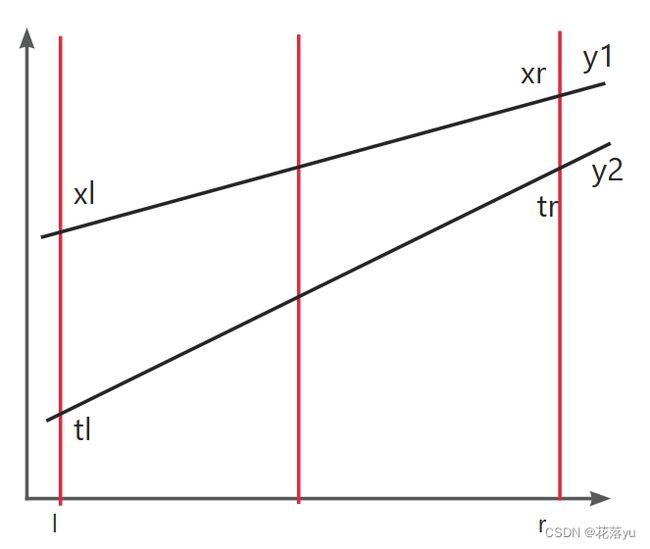
如果根节点不为空，我们就需要进行线段之间的比较了，代码注释里的当前线段也就是当前根节点记录的线段。tl <= xl && tr <= xr的情况如下图所示，此时在区间[l,r]内，根节点记录的线段y2，纵坐标的值一直小于当前要插入的线段y1，因为我们记录的是最小值，所以根节点不用更新，直接返回即可。

情况3

else if (tl >= xl && tr >= xr) {//当前线段的值全部在要插入线段的上面，则全部用插入线段x更新
		t.x = x;
		return t;} 

tl >= xl && tr >= xr的情况如下，和情况（2）刚好相反，在[l,r]区间内，待插入线段的y值都小于根节点记录线段的y值，那么更新当前根节点记录的线段为待插入线段，即t.x = x，然后返回。

情况4

很明显，我们上面考虑的情况，根节点记录的线段和待插入的线段在区间内是不相交的，接下来，我们要考虑的是，两个线段在区间内相交的情况，因为我们记录的是在区间内中点取得最大值的线段，所以我们要比较两个线段在区间中点处的取值。

long m = (l + r) >> 1;
long tm = t.x.query(m);//当前线段的中点值
long xm = x.query(m);//插入线段的中点值

情况4.1

if (tm > xm) {//根节点的线的值大于当前线的值 当前线段的中点值大于插入线段的中点值
					Line xx = t.x;
					t.x = x;//更新根节点的线为当前线
					if (xl >= tl) {//当前点的最左边的值大于等于根节点的最左边的值
						t.l = addLine(t.l, xx, l, m, tl, tm);//更新左端点
					} else {
						t.r = addLine(t.r, xx, m + 1, r, tm + x.a, tr);//更新右端点
					}
				}

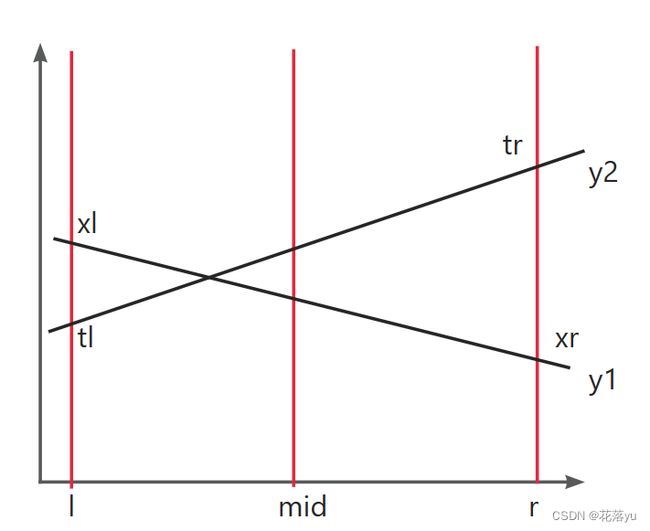
第一种情况是根节点记录的线段在中点处的值大于带插入线段中点处的值，那么就要用待插入线段更新根节点，重要的是，我们不仅仅要更新根节点，如下图所示，

我们通过这个图可以看出，在该树的右区间内一直是根节点记录的线段在待插入线段的上方，这和我们在此处的更新是相同的，但是在该树的左区间，出现了两个线段的交点，这就导致，根节点记录的线段与待插入线段的y值的大小关系出现了变化，所以我们应该继续向左区间进行更新，也就是出现交点的区间。

刚刚我们是根据图进行分析的，那么我们怎么通过代码，来确定两个线段的交点是在哪一个区间呢，那就是中点处两个线段的大小关系，因为交点处的大小关系发生了变化，所以我们只需要查找大小关系发生变化的区间就可以了。

终点处的大小关系为tm > xm，那么当左边界的大小关系为xl >= tl时表示，在左区间存在交点。

我们解决了第一个问题，即往哪一个区间更新，接下来有第二个问题，传参。

t.l = addLine(t.l, xx, l, m, tl, tm);这是向左区间进行更新时传的参数，这里面不好理解的是xx，可以看到xx表示的是当前根节点记录的线段，那么我们为什么不把待插入线段传过去，而是要传当前根节点记录的线段呢，因为进行了根节点更新后，待插入线段已经被该子树的根节点记录了，那么我在后面的节点中就不需要考虑该线段了，我只需要考虑原来根节点记录的线段，在后续节点中是否会变为“优势线段”就可以了。

t.r = addLine(t.r, xx, m + 1, r, tm + x.a, tr);这是向右区间进行更新时传的参数，这里不好理解的是tm + x.a，右区间横坐标的范围其实是[mid+1,r]，tm=a*mid+b，而此时右区间的左边界应该是a*（mid+1）+b=a*mid+a+b=tm+a。

情况4.2

这种情况就是根节点记录的线段在中点处的值小于带插入线段中点处的值，此时我不需要更新根节点的值，但是我依然要进行向下更新，因为在某个区间存在交点，使线段之间的大小关系发生变化，基本原理和情况4.1的情况一样，只是此时下传的线段应该是待插入线段。

else {
	if (tl >= xl) {//当前点的最左边的值小于等于根节点的最左边的值
		t.l = addLine(t.l, x, l, m, xl, xm);//更新左端点
	} else {
		t.r = addLine(t.r, x, m + 1, r, xm + x.a, xr);//更新右端点
		}
	}

插入操作的全部代码如下：

private Node addLine(Node t, Line x, long l, long r, long xl, long xr) {
			//根节点，线，左端点，右端点，左边界，右边界；xl=a*l+b;xr=a*r+b
			if (t == null)
				return new Node(x);
			long tl = t.x.query(l);//当前线段的左边界值
			long tr = t.x.query(r);//当前线段的右边界值
			if (tl <= xl && tr <= xr) {//当前线段的值全部在要插入线段的下面，则不用更新
				return t;
			} else if (tl >= xl && tr >= xr) {//当前线段的值全部在要插入线段的上面，则全部用插入线段x更新
				t.x = x;
				return t;
			} else {//否则半边全部更新，半边继续看是否要更新
				long m = (l + r) >> 1;
				long tm = t.x.query(m);//当前线段的中点值
				long xm = x.query(m);//插入线段的中点值
				if (tm > xm) {//根节点的线的值大于当前线的值 当前线段的中点值大于插入线段的中点值
					Line xx = t.x;
					t.x = x;//更新根节点的线为当前线
					if (xl >= tl) {//当前点的最左边的值大于等于根节点的最左边的值
						t.l = addLine(t.l, xx, l, m, tl, tm);//更新左端点
					} else {
						t.r = addLine(t.r, xx, m + 1, r, tm + x.a, tr);//更新右端点
					}
				}else {
					if (tl >= xl) {//当前点的最左边的值小于等于根节点的最左边的值
						t.l = addLine(t.l, x, l, m, xl, xm);//更新左端点
					} else {
						t.r = addLine(t.r, x, m + 1, r, xm + x.a, xr);//更新右端点
					}
				}
				return t;
			}
		}

查询最值

当横坐标为x时，所有线段中取到的最值，依然以最小值为例。

public long minimize(long x) {
			Node t = root;
			long l = low;
			long r = high;
			long ret = Long.MAX_VALUE;
			while (t != null && l < r) {
				ret = Math.min(ret, t.x.query(x));
				long m = (l + r) >> 1;
				if (x <= m) {//向左节点找
					t = t.l;
					r = m;
				} else {//向右节点找
					t = t.r;
					l = m + 1;
				}
			}
			return ret;
		}

该操作的主要做法为对所有包含横坐标为x的位置的区间上的最优势线段计算答案，最后取所有答案里的最小值。

我们可以这么理解，根节点记录的线段是当前区间的最优势线段，在对该区间的子区间进行更新时，我并没有下传当前区间记录的线段，这个操作有一点类似懒标记，那么我在查找的时候，查找过程经历的所有区间所记录的线段都可以看作是一个懒标记，此时我需要下传懒标记了，也就是这个区间的线段有可能是我们的答案，那么我们就要求一下这个线段在x处的y值，并且与当前记录的答案作比较，即ret = Math.min(ret, t.x.query(x));。