Logistic 回归算法

Logistic 回归算法

Logistic 回归简述

Logistic 回归是一种用于解决二分类问题的机器学习算法。虽然 Logistic Regression 中包含了 Regression 一词，但实际上逻辑回归是一种用于分类的方法，而不是回归。

Logistic 回归通过建立一个逻辑回归模型来预测离散的输出变量，该输出变量可以是 0 或 1。具体来说，该模型基于输入特征的线性组合，通过拟合一个逻辑函数（通常是 sigmoid 函数）将线性组合映射到 [0, 1] 的概率范围内，从而预测输入特征与离散输出变量之间的关系，并将输出映射到 0 或 1 两个不同的类别。

假设现在有一些数据点，我们利用一条直线对这些数据点进行拟合（该直线称为最佳拟合直线），这个拟合过程就称作为回归。如下图所示：

利用逻辑回归模型进行分类的主要思想：根据现有数据，对分类边界建立回归公式，以此进行分类。

Sigmoid 函数

想了解 Logistic 回归，首先需要了解 sigmoid 函数，其公式如下：
$$f(x)=\frac{1}{1+e^{-x}}$$
sigmoid 函数曲线如下图所示：

Logistic 回归模型表达式

逻辑回归模型从本质上来说是一个基于条件概率的判别模型，逻辑回归模型的数学表达式如下：
$$\begin{gathered} p(y=1|x)=\frac{1}{1+e^{(-z)}} \\ p(y=0|x)=1-p(y=1|x) \end{gathered}$$
其中，$p(y=1|x)$ 表示给定输入 $x$ 时，输出变量 $y=1$ 的概率，$z$ 表示输入特征 $x$ 的线性组合加上一个偏置项 $b$，即 $z=\sum _i^n{w}_i{x}_i+b$。$w_i$ 为特征 $x_i$ 的权重，通过对训练数据进行最大似然估计或梯度下降等优化，可以确定最佳的权重参数 $w$ 和偏置项 $b$。

如果我们把 $z$ 展开，那么可以得到如下：
$$
z = \begig{bmatrix} \theta_0
&\theta_1 &\cdots &\theta_n
\end{bmatrix}\begin{bmatrix}x_0
\ x_1
\ \vdots
\ x_n

\end{bmatrix} + b = \theta^Tx + b
$$

$$h_{\theta }(x)=g({\theta }^{T}x+b)=g(z)=\frac{1}{1+e^{-z}}$$

其中，$\theta$ 是参数列向量（要求解的），$x$ 是样本列向量（给定的数据集）。通过 sigmoid 函数可以将任意实数映射到 [0, 1] 区间。$h_{\theta }(x)$ 给出了输出变量为 $1$ 的概率，比如 $h_{\theta }(x)=0.7$ 表示有 $70\%$ 的概率判定类别为 $1$，有 $30\%$ 的概率判定类别为 $0$。

现在给出一个新的样本，如果我们能找到合适的参数列向量 $\theta ([{\theta }_0,{\theta }_1,...,{\theta }_n])$，那么我们就可以将样本数据直接代入 sigmoid 函数中进行求解，得到其类别为 $1$ 或 $0$ 的概率，进而判定其所属类别。

求解参数 $\theta $

那么问题来了，我们该如何得到合适的参数向量 $\theta$？根据逻辑回归模型的表达式，可以得到如下：
$$\begin{gathered} p(y=1|x;\theta )=h_{\theta }(x) \\ p(y=0|x;\theta )=1-h_{\theta }(x) \end{gathered}$$
理想状态下，我们希望对每个样本的类别预测概率均为 $1$，也就是完全分类正确。但在实际情况中，很难做到如此完美，样本的类别预测概率越接近 $1$，其分类结果越准确。一个样本属于正样本的概率为 $0.51$，我们可以说它是正样本；另一个样本属于正样本的概率为 $0.99$，我们也可以说它是正样本；但显然，第二个样本的预测概率更高，更具说服力。我们可以将上述两个类别的条件概率合二为一，得到如下：
$$Loss(h_{\theta }(x),y)=h_{\theta }(x{)}^y(1-h_{\theta }(x){)}^{(1-y)}$$
我们称上式为损失函数（Loss Function）。当 $y=1$ 时，第二项为 $0$；当 $y=0$ 时，第一项为 $0$。为了简化问题，我们可以对整个表达式进行求对数，得到如下：
$$Loss(h_{\theta }(x),y)=y\log h_{\theta }(x)+(1-y)\log (1-h_{\theta }(x))$$
上述损失函数是对于一个样本而言的。假定样本之间相互独立，那么整个样本集的预测概率即为所有样本预测概率的乘积，基于此，可得到如下公式：
$$J(\theta )=\sum _i^m{y}^{(i)}\log (h_{\theta }(x^{(i)}))+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))$$

$$-J(\theta )=-\sum _i^m{y}^{(i)}\log (h_{\theta }(x^{(i)}))+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))$$

其中，$m$ 为样本总数，$y^{(i)}$ 表示第 $i$ 个样本的类别，$x^{(i)}$ 表示第 $i$ 个样本。由此可以得出，满足 $J(\theta )$ 最大或满足 $-J(\theta )$ 最小的 $\theta$ 值就是我们需要求解的答案。

为了使得 $J(\theta )$ 最大，我们可以使用最大似然估计、梯度上升或梯度下降优化算法求解参数 $\theta$。当损失函数为 $J(\theta )$ 时，可以使用梯度上升算法对参数 $\theta$ 进行优化；当损失函数为 $-J(\theta )$ 时，可以使用梯度下降算法对参数 $\theta$ 进行优化。

梯度上升优化算法

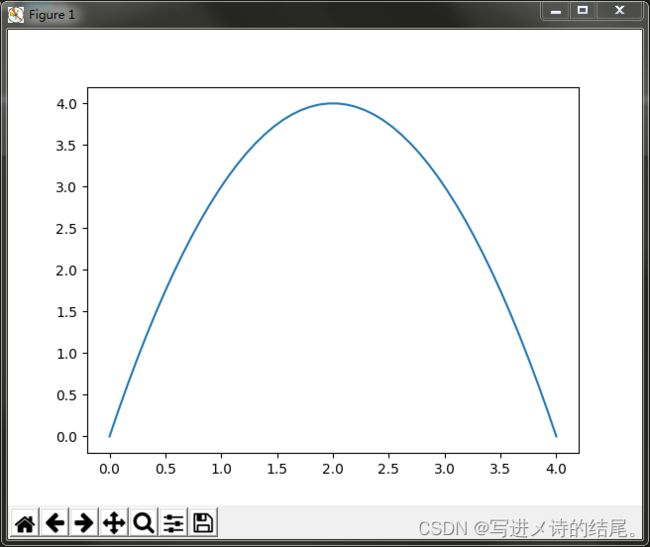
假设存在一个函数 $f(x)=-x^2+4x$，如何计算该函数的极值？该函数的曲线如下图所示：

显然该函数的曲线开口向下，存在极大值。我们可以运用中学所学的知识对其求极值，其导数为 $f^{\prime }(x)=-2x+4$，令导数为 $0$，可得出 $x=2$ 即为该函数的极大值点，且极大值为 $4$。

但在实际情况中，函数不会像上面那样简单，就算求出了函数的导数，也很难精确计算出函数的极值，此时可以考虑用迭代的方法逼近极值。这种通过迭代逼近寻找最佳拟合参数的方法就叫做最优化算法。值更新的公式表示如下：
$$x_{i+1}=x_i+\alpha \cdot \frac{\partial f(x_i)}{x_i}$$
其中，$\alpha$ 为步长，也就是学习率（Learning Rate），用于控制更新的幅度。更新示意图如下所示：

比如从 $(0,0)$ 开始，迭代路径为 1 -> 2 -> 3 -> 4 -> ··· -> n，直到求出的 $f(x)$ 为函数极大值的近似值。迭代逼近函数极大值的代码实现如下：

# 梯度上升
def gradient_ascent(alpha=0.01, precision=0.00000001):
    """
    :param alpha: 学习率
    :param precision: 停止迭代的阈值
    :return: 逼近函数极值的极值点
    """
    # 偏导表达式
    def partial_derivative(x_old):
        return -2 * x_old + 4

    x_old = -1  # 初始值，给一个小于 x_new 的值
    x_new = 0  # 梯度上升的起点，即从 (0, 0) 开始

    while abs(x_new - x_old) > precision:
        x_old = x_new
        x_new = x_old + alpha * partial_derivative(x_old)

    return x_new


if __name__ == '__main__':
    result = gradient_ascent()
    print(result)
---------
1.999999515279857

从上面可以看出，结果已经非常接近真实极值点 $x=2$，上述用到的就是梯度上升优化算法。同理，$J(\theta )$ 这个损失函数的极值点也可以这样求出，只要计算出 $J(\theta )$ 的偏导，就可以利用梯度上升算法，求解出 $J(\theta )$ 的极大值。

$J(\theta )$ 关于 $\theta$ 的偏导，求解过程如下：
$$\frac{\partial J(\theta )}{{\theta }_j}=\frac{\partial J(\theta )}{\partial g({\theta }^{T}x)}\ast \frac{\partial g({\theta }^{T}x)}{\partial {\theta }^{T}x}\ast \frac{\partial {\theta }^{T}x}{\partial {\theta }_j}$$
其中，
$$\frac{\partial J(\theta )}{\partial g({\theta }^{T}x)}=y\ast \frac{1}{g({\theta }^{T}x)}+(y-1)\ast \frac{1}{1-g({\theta }^{T}x)}$$

$$g^{\prime }(z)=\frac{d\frac{1}{1+e^{-z}}}{dz}=g(z)(1-g(z))⟹\frac{\partial g({\theta }^{T}x)}{\partial {\theta }^{T}x}=g({\theta }^{T}x)(1-g({\theta }^{T}x))$$

$$\frac{\partial {\theta }^{T}x}{{\theta }_j}=\frac{\partial J({\theta }_1{x}_1+{\theta }_2{x}_2+\cdots +{\theta }_n{x}_n)}{\partial {\theta }_j}=x_j$$

综上可得，
$$\frac{\partial J(\theta )}{{\theta }_j}=(y-h_{\theta }(x))x_j$$
上述即为 $J(\theta )$ 关于 $\theta$ 的偏导，有了偏导，我们可以进一步推导出梯度上升中的值更新公式：
$${\theta }_{j\_new}={\theta }_{j\_old}+\alpha \cdot \sum _{i=1}^m(y^{(i)}-h_{\theta }(x^{(i)}))x_j^{(i)}$$
有了上述这些公式，我们就可以编写代码，计算出损失函数的最佳拟合参数。

Logistic 回归简单实现

有一个简单的数据集，其数据格式如下图所示：

该数据集共有三列数据，前两列为特征数据，最后一列为标签数据。我们可以将第一列特征数据看作 $x$ 轴上的值，将第二列特征数据看作 $y$ 轴上的值，根据对应标签的不同，对这些样本点进行分类。

代码实现如下：

import numpy as np
import matplotlib.pyplot as plt


# 读取数据集
def read_dataset(file_path: str) -> (list, list):
    """
    :param file_path: 数据集的路径
    :return: 训练数据，训练标签
    """
    data = []  # 用于存储特征数据；(100, 3)；三列分别表示 w0（偏置项）、w1（第一列特征数据权重）、w2（第二列特征数据权重）
    labels = []  # 用于存储标签数据；(100,)

    file = open(file_path)
    for line in file.readlines():
        line_list = line.strip().split()
        data.append([1.0, float(line_list[0]), float(line_list[1])])
        labels.append(int(line_list[2]))
    file.close()

    return data, labels


# 绘制样本分布图
def data_distribution(data: list, labels: list) -> None:
    """
    :param data: 训练数据
    :param labels: 训练标签
    :return: 数据分布图
    """
    data_arr = np.array(data)  # 转成数组
    num_samples = data_arr.shape[0]  # 获取样本个数

    x0_feature = []  # 存放标签为 0 的第一列中的特征数据
    y0_feature = []  # 存放标签为 0 的第二列中的特征数据
    x1_feature = []  # 存放标签为 1 的第一列中的特征数据
    y1_feature = []  # 存放标签为 1 的第二列中的特征数据

    for i in range(num_samples):
        if labels[i] == 1:  # 1 为正样本
            x1_feature.append(data[i][1])
            y1_feature.append(data[i][2])
        else:  # 0 为负样本
            x0_feature.append(data[i][1])
            y0_feature.append(data[i][2])

    # 绘图
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(x1_feature, y1_feature, s=20, c='r', marker='s', alpha=.5)
    ax.scatter(x0_feature, y0_feature, s=20, c='g', alpha=.5)
    plt.title('data distribution')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()


# sigmoid 函数
def sigmoid(z):
    """
    :param z: 目标值表达式
    :return: sigmoid 表达式
    """
    return 1.0 / (1 + np.exp(-z))


# 梯度上升
def gradient_ascent(data: list, labels: list, alpha=0.001, num_iteration=500) -> np.ndarray:
    """
    :param data: 训练数据
    :param labels: 训练标签
    :param alpha: 学习率
    :param num_iteration: 迭代次数
    :return: 参数权重
    """
    data_mat = np.mat(data)  # 转成矩阵
    labels_mat = np.mat(labels).transpose()  # 转成矩阵，并进行转置

    n = data_mat.shape[1]  # data 的列数；3

    weights = np.ones((n, 1))  # 有几个特征就有几个参数，这里有 3 个特征，因此有 3 个参数

    # 训练模型，得到参数权重
    for i in range(num_iteration):
        h = sigmoid(data_mat * weights)  # 预测值；(100, 1)
        error = labels_mat - h  # 真实值 - 预测值；(100, 1)
        weights = weights + alpha * data_mat.transpose() * error  # w_new = w_old + α * x^T * (y - y')

    return weights.getA()  # 将矩阵转换为数组，并返回权重数组


# 通过求解出的参数（回归系数），可以确定不同类别数据之间的分隔线，从而绘制出决策边界
def decision_boundary(data: list, labels: list, weights: np.ndarray) -> None:
    """
    :param data: 训练数据
    :param labels: 训练标签
    :param weights: 参数权重
    :return: 决策边界图
    """
    data_arr = np.array(data)  # 转成数组
    num_samples = data_arr.shape[0]  # 获取样本个数

    x0_feature = []  # 存放标签为 0 的第一列中的特征数据
    y0_feature = []  # 存放标签为 0 的第二列中的特征数据
    x1_feature = []  # 存放标签为 1 的第一列中的特征数据
    y1_feature = []  # 存放标签为 1 的第二列中的特征数据

    for i in range(num_samples):
        if labels[i] == 1:  # 1 为正样本
            x1_feature.append(data[i][1])
            y1_feature.append(data[i][2])
        else:  # 0 为负样本
            x0_feature.append(data[i][1])
            y0_feature.append(data[i][2])

    # 绘图
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(x1_feature, y1_feature, s=20, c='r', marker='s', alpha=.5)
    ax.scatter(x0_feature, y0_feature, s=20, c='g', alpha=.5)
    x = np.arange(-3.0, 3.0, 0.1)
    y = -(weights[0] + weights[1] * x) / weights[2]
    ax.plot(x, y)
    plt.title('best fit')
    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.show()


if __name__ == '__main__':
    file_path = r'D:\MachineLearning\testSet.txt'

    # 获取训练数据和训练标签
    data, labels = read_dataset(file_path)

    # 查看样本分布
    # data_distribution(data, labels)

    # 获取权重
    weights = gradient_ascent(data, labels)  # 得到一个形状为 (3, 1) 的权重数组
    print(weights)

    # 查看决策边界
    decision_boundary(data, labels, weights)


"""
weights 是一个包含三个元素的数组 [w0, w1, w2]，其中 w0 是偏置项（或者称为截距），w1 和 w2 分别是特征一和特征二的权重；
在二维空间中，线性分类器的决策边界通常是一条直线，其方程可以表示为 w0 + w1*x1 + w2*x2 = 0，其中 (x1, x2) 是特征一和特征二的取值；
将上述方程稍作变换，就可以得到 - (w0 + w1*x) / w2，其中 x = x1，也就是特征一的取值。这个表达式描述了特征一和特征二之间的决策边界，可以用来在二维平面上画出分类器的决策边界直线。
"""
---------
[[ 4.12414349]
 [ 0.48007329]
 [-0.6168482 ]]

上述代码在进行梯度上升优化时，每次都需要计算整个数据集，计算复杂度太高，我们可以使用随机梯度上升算法对其进行改进。主要改进有两点，第一点是动态调整学习率，使得学习率随着迭代次数的增加而减小；第二点是使用一个样本数据进行参数的更新，样本数据随机选取，且下一次迭代将从未使用过的样本点中选取。随机梯度上升算法可以有效地减少计算量，并保证回归效果。

经过综合对比，我们可以得到以下结论：

• 当数据集较小时，使用梯度上升算法效果较好
• 当数据集较大时，使用改进的随机梯度上升算法效果较好

使用 sklearn 构建 Logistic 回归分类器

sklearn.linear_model 模块实现了 Logistic 回归算法，不仅如此，该模块还提供了很多模型供我们使用，比如 Lasso 回归、脊回归等。LogisticRegression 函数实现如下所示：

sklearn.linear_model.LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)
	- penalty：有 l1、l2、elasticnet、None 四个值可供选择，默认为 l2；l1 表示添加 l1 正则化，假设模型的参数满足拉普拉斯分布；l2 表示添加 l2 正则化，假设模型的参数满足高斯分布；elasticnet 表示添加 l1 和 l2 正则化；None 表示不添加正则项；所谓的正则项就是对参数施加一种约束，使得模型避免发生过拟合的现象，但是不一定加约束就更好，只能说在加约束的情况下，理论上应该可以获得泛华能力更强的结果
    - dual：布尔值，默认为 False；二元公式仅适用于 liblinear 求解器的 l2 惩罚，当 n_samples > n_features 时，首选 dual=False
    - tol：停止求解的标准，即求解到多少认为已经求出最优解，默认为 1e-4；
    - C：正则化强度的倒数，必须是正浮点数，默认为 1.0；与 SVM 一样，数值越小，正则化强度越大
    - fit_intercept：是否存在截距或偏差，即偏置项，默认为 True
    - intercept_scaling：只有在使用求解器 liblinear 且 fit_intercept=True 时才有用，默认为 1
    - class_weight：用于标示分类模型中各种类型的权重，可以是一个字典或 balanced 字符串，默认为 None；举个例子，对于 0、1 的二元模型，我们可以定义 class_weight={0: 0.9, 1: 0.1}，这样类型 0 的权重为 90%，而类型 1 的权重为 10%；如果 class_weight 选择 balanced，那么类库会根据训练样本量来计算权重，某种类型样本量越多，则权重越低，样本量越少，则权重越高，类权重计算方法为 n_samples / (n_classes * np.bincount(y))，n_samples 为样本数，n_classes 为类别数量，np.bincount(y) 会输出每个类的样本数，例如 y=[1, 0, 0, 1, 1]，则 np.bincount(y)=[2, 3]
    - random_state：随机数种子，默认为 None；仅在 solver 为 sag、saga、liblinear 时有用
    - solver：优化算法，默认为 lgfgs；对于小数据集，liblinear 是个不错的选择，而对于大数据集，sag 和 saga 速度更快；对于多分类问题，只有 newton-cg、sag、saga、lbfgs 能够处理多项式损失，而 liblinear 受限于一对剩余（OvR），就是用 liblinear 的时候，如果是多分类问题，得先把一种类别作为一个类别，剩余的所有类别作为另外一个类别，依次类推，遍历所有类别，从而进行分类；newton-cg、sag、lbfgs 这三种优化算法都需要损失函数的一阶或者二阶连续导数，因此不能用于没有连续导数的 L1 正则化，只能用于 L2 正则化，而 liblinear 和 saga 通吃 L1 和 L2 正则化；liblinear 使用了开源的 liblinear 库，内部使用了坐标轴下降法来迭代优化损失函数；lbfgs 是拟牛顿法的一种，利用损失函数二阶导数矩阵（即海森矩阵）来迭代优化损失函数；newton-cg 是牛顿法家族中的一种，利用海森矩阵来迭代优化；sag 是随机平均梯度下降，属于梯度下降法的变种，与普通梯度下降法的区别是每次迭代仅用一部分样本来计算梯度，适用于样本量多的情况；saga 是线性收敛的随机优化算法的变种
    - max_iter：算法收敛的最大迭代次数，默认为 100
    - multi_class：分类方式，有 auto、ovr、multinomial 可供选择，默认为 auto；如果选择的是 ovr，那么每个标签都会拟合出一个二元问题；当求解器为 liblinear 时，multinomial 不可用；如果数据是二元的，或者求解器为 liblinear，auto 会选择 ovr，其他情况则选择 multinomial
    - verbose：日志冗长度，默认为 0，即不输出训练过程；为 1 的时候偶尔输出结果；大于 1 时对每个子模型都输出结果
    - warm_start：热启动参数，默认为 False；如果为 True，则下一次训练以追加树的形式进行
    - n_jobs：并行数，默认为 1；如果为 2，则表示用 CPU 的 2 个内核运行程序；如果为 -1，则表示用所有内核运行
    - l1_ratio：elasticnet 的混合参数，仅在 penalty=elasticnet 时使用；如果为 0，则表示使用 l2 正则化

由 LogisticRegression 创建的实例对象 clf 具有以下方法：

decision_function(X)  # 预测样本的置信度得分
	- X：训练数据，形状为 (n_samples, n_features)
	返回形状为 (n_samples, n_classes) 的置信度得分

densify()  # 将系数矩阵转换为密集数组格式

fit(X, y, sample_weight=None)  # 根据训练集拟合分类器
	- X：训练数据，形状为 (n_samples, n_features)
    - y：目标值（训练样本对应的标签），形状为 (n_samples,)
    - sample_weight：样本权重，如果为 None，则样本权重相同
    返回拟合的逻辑回归分类器

get_params(deep=True)  # 以字典形式返回 MultinomialNB 类的参数
	- deep：布尔值，默认为 True
    返回参数

predict(X)  # 预测所提供数据的类别标签
	- X：预测数据，形状为 (n_samples, n_features)
    以 np.ndarray 形式返回形状为 (n_samples,) 的每个数据样本的类别标签
    
predict_log_proba(X)  # 返回预测数据 X 在各类别标签中所占的对数概率
	- X：预测数据，形状为 (n_samples, n_features)
    返回该样本在各类别标签中的预测对数概率，类别的顺序与属性 classes_ 中的顺序一致
    
predict_proba(X)  # 返回预测数据 X 在各类别标签中所占的概率
	- X：预测数据，形状为 (n_samples, n_features)
    返回该样本在各类别标签中的预测概率，类别的顺序与属性 classes_ 中的顺序一致
    
score(X, y, sample_weight=None)  # 返回预测结果和标签之间的平均准确率
	- X：预测数据，形状为 (n_samples, n_features)
    - y：预测数据的目标值（真实标签）
    - sample_weight：默认为 None
    返回预测数据的平均准确率，相当于先执行了 self.predict(X)，而后再计算预测值和真实值之间的平均准确率

from sklearn.linear_model import LogisticRegression


def colicSklearn():
    frTrain = open(r'D:\MachineLearning\horseColicTraining.txt')  # 打开训练集
    frTest = open(r'D:\MachineLearning\horseColicTest.txt')  # 打开测试集

    trainingSet = []
    trainingLabels = []
    testSet = []
    testLabels = []

    for line in frTrain.readlines():
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(len(currLine) - 1):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[-1]))

    for line in frTest.readlines():
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(len(currLine) - 1):
            lineArr.append(float(currLine[i]))
        testSet.append(lineArr)
        testLabels.append(float(currLine[-1]))
    classifier = LogisticRegression(solver='liblinear', max_iter=10).fit(trainingSet, trainingLabels)
    test_accurcy = classifier.score(testSet, testLabels) * 100

    print('正确率:%f%%' % test_accurcy)


if __name__ == '__main__':
    colicSklearn()
---------
正确率:73.134328%

Logistic 回归算法的优缺点

优点

1. 算法简单易于理解和实现，计算效率高。
2. 可以处理二分类和多分类问题。
3. 对特征之间的关联性不敏感，适用于处理高维数据。
4. 输出结果具有概率解释，可以用于判断样本属于某个类别的概率。

缺点

1. 假设特征与目标变量之间存在线性关系，无法处理非线性关系。
2. 对异常值和缺失值比较敏感，需要进行数据预处理。
3. 容易出现欠拟合或过拟合的情况，需要进行正则化处理。
4. 无法处理特征之间的交互作用。