递归实现归并排序与测试各类排序的性能
目录
基本思想
代码实现
时空复杂度
测试各排序性能
基本思想
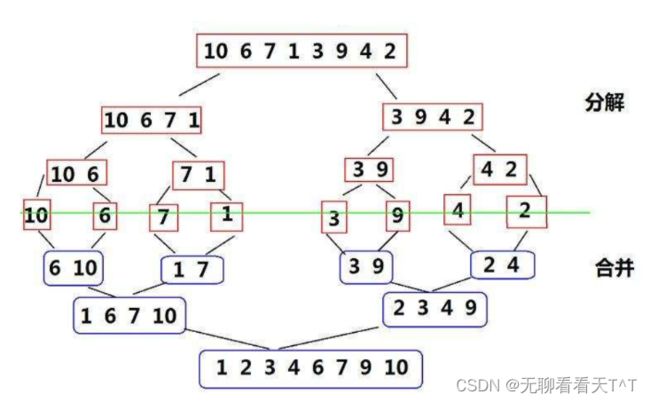
将待排序的数组不断二分,直到每个子数组只包含一个元素或为空。然后通过合并操作将这些子数组逐步合并成较大的有序数组,最终得到完全有序的结果:
下面是递归版本的归并排序实现基本思路:
1、分解:将待排序的数组从中间位置切割成两个子数组
- 找到中间位置 mid = (left + right) / 2
- 递归地对左半部分进行归并排序:mergeSort(arr, left, mid)
- 递归地对右半部分进行归并排序:mergeSort(arr, mid+1, right)
2、合并:将两个已经排好序的子数组合并为一个有序数组
- 创建一个临时空间 temp[] 来存储合并结果
- 初始化指针 i 指向左半部分起始位置 left,指针 j 指向右半部分起始位置 mid+1
- 对于 k = left 到 right 的范围
- 如果 arr[i] <= arr[j],则把 arr[i] 放入 temp[k] 中,并增加 i 和 k 的值
- 否则把 arr[j] 放入 temp[k] 中,并增加 j 和 k 的值
3、复制:将临时空间 temp[] 中的元素复制回原数组 arr[]
- 对于 k = left 到 right 的范围,把 temp[k] 复制到 arr[k]
4、重复执行上述步骤,直到每个子数组只包含一个元素或为空
代码实现
//归并排序(递归部分)
void _MergeSort(int* a, int begin, int end, int* tmp)
{
//当递归至只有一个元素时就返回
if (begin >= end)
return;
//找到中间位置
int mid = (begin + end) / 2;
// [begin, mid][mid+1, end]
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
// [begin, mid][mid+1, end]归并
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
//归并排序主体函数
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}时空复杂度
最坏时间复杂度:O(N*logN)(logN层,递归N次,N*logN)
空间复杂度:O(N)(归并排序需要额外的空间来存储临时结果和辅助变量。对于每一层递归调用,在合并阶段都需要创建一个与原始输入大小相同的临时数组来存储结果,并在每次迭代结束后释放该内存。因此,在最坏情况下,即所有层级上同时存在(但不重叠)的子问题数量达到最大时,所需额外空间总量达到 O(n) 级别
)
测试各排序性能
void TestOP()
{
srand(time(0));
const int N = 10000000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
}
int begin1 = clock();
//InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
//SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort(a5, 0, N - 1);
int end5 = clock();
int begin6 = clock();
MergeSort(a6, N);
int end6 = clock();
int begin7 = clock();
//BubbleSort(a7, N);
int end7 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("QuickSort:%d\n", end5 - begin5);
printf("MergeSort:%d\n", end6 - begin6);
printf("BubbleSort:%d\n", end7 - begin7);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
free(a7);
}~over~