查找与排序

二分查找

注意：使用二分查找的前提是数组有序！！！

手撕二分查找

有序数组或对时间复杂度的要求有 log，通常用二分查找。
基本思路是每次取中间，如果等于目标即返回，否则根据大小关系切去一半，时间复杂度是O(logn)，空间复杂度O(1)。
以简单例题为例：
35. 搜索插入位置
【题目描述】给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
解答：
找最小中的最大值或最大中的最小值，用两段二分法，两段二分法的模板主要有以下两种，区别在于“ l < r 与 r = mid” 或者 “l <= r 与 r = mid - 1” 。

int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int l = 0, r = n - 1;
        while(l < r){
            //等价于mid = (r - l) / 2 + l，防止加和溢出;
            int mid = ((r - l) >> 1) + l; //移位运算符除法速度快
            if(nums[mid] < target){
            //注意这里必须对 l 做改变，r可不变。
            //因为当仅剩两个数l , r时，每次mid都会选到左边的数l，
            //l不做出改变的话，就会陷入死循环
                l = mid + 1; 
            }
            else{
                r = mid;
            }
        } //r == l时循环结束，此时r 与l 都是结果
        return l;
    }

int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int l = 0, r = n - 1;
        while(l <= r){
            //右移一位等价于除以2，>>符号优先级最低，需要加括号。
            //等价于mid = (r - l) / 2 + l，防止加和溢出;出;
            int mid = ((r - l) >> 1) + l; //移位运算符除法速度快
            if(nums[mid] < target){
                l = mid + 1;
            }
            else{
                r = mid - 1;
            }
        } //l == r + 1时循环结束，此时l 与 r + 1都是结果
        return l;
    }

注意点：
1）右移一位等价于除以2，>>符号优先级最低，需要加括号。
2） mid = ((r-l)>>1)+l; //移位运算符除法速度快
3）等价于mid = (r-l)/2+l，这样写防止l和r太大时，加和溢出;

代码解释：根据 if 的判断条件，l 左边的值一直保持小于target，r 右边的值一直保持大于等于target，而且 l 最终一定等于 r +1，这么一来，循环结束后，在 l 和 r 之间画一条竖线，恰好可以把数组分为两部分：l 左边的部分和 r 右边的部分，而且 l 左边的部分全部小于target，并以 结尾；r 右边的部分全部大于等于target，并以 l 为首。所以最终答案一定在 l 的位置。
每次循环，至少会把区间[ l , r ]的长度减少1。当 l = r 时，mid= l = r。因为mid在每次循环中始终在[ l, r ]之间，所以mid-1最小为 l-1，mid+1最大为 r+1。
如果感觉不好理解的话，可以使用完整通用版二分查找：

int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int l = 0, r = n - 1;
        while(l <= r)
        {
            int mid = (r - l) / 2 + l; //用移位运算符除法的话速度更快
            if(nums[mid] < target)
            {
                l = mid + 1;
            }
            else if(nums[mid] > target)
            {
                r = mid - 1;
            }
            else
            {
            	return mid;
            }
        }
        return l;
    }

进阶版二分查找：
找最小中的最大值或最大中的最小值，用两段二分
875. 爱吃香蕉的珂珂
珂珂喜欢吃香蕉。这里有 n 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 h 小时后回来。
珂珂可以决定她吃香蕉的速度 k （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 k 根。如果这堆香蕉少于 k 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。
珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在 h 小时内吃掉所有香蕉的最小速度 k（k 为整数）。

示例 1：
输入：piles = [3,6,7,11], h = 8
输出：4

【思路】
由于吃香蕉的速度和是否可以在规定时间内吃掉所有香蕉之间存在单调性，因此可以使用二分查找的方法得到最小速度 k。

由于每小时都要吃香蕉，即每小时至少吃 1 个香蕉，因此二分查找的下界是 1；由于每小时最多吃一堆香蕉，即每小时吃的香蕉数目不会超过最多的一堆中的香蕉数目，因此二分查找的上界是最多的一堆中的香蕉数目。

假设吃香蕉的速度是 $\text{k}$，则当一堆香蕉的个数是 $\text{pile}$ 时，吃掉这堆香蕉需要 $\lceil \frac{\text{pile}}{\text{k}}\rceil$小时，由此可以计算出吃掉所有香蕉需要的时间。如果在速度 $\text{k}$ 下可以在 h 小时内吃掉所有香蕉，则最小速度一定小于或等于 $\text{k}$，因此将上界调整为 $\text{k}$；否则，最小速度一定大于$\text{k}$，因此将下界调整为 $\text{k}+1$。
二分查找结束之后，即可得到在 h 小时内吃掉所有香蕉的最小速度 k。

【除法向上取整的技巧】
实现方面，在计算吃掉每一对香蕉的时间时，由于 $\text{pile}$ 和 $\text{k}$ 都大于 0，因此 $\lceil \frac{\text{pile}}{\text{k}}\rceil$ 等价于 $\lfloor \frac{\text{pile}+\text{k}-1}{\text{k}}\rfloor$，即可以用(piles[i] + k - 1) / k 来实现 $\lceil \frac{\text{pile}}{\text{k}}\rceil$ 的ceil 运算。

int minEatingSpeed(vector<int>& piles, int h) {
        int n = piles.size();
        sort(piles.begin(), piles.end());
        int l = 1, r = piles[n - 1];
        while(l < r){
            int k = ((r - l) >> 1) + l;
            long sum = 0;                 //long类型
            for(int i = 0; i < n; ++i){              
                sum += (piles[i] + k - 1) / k;     
                //sum += ceil(piles[i] / float(k));这样求上界可能有误
            }
            if(sum > h){  //找最小中的最大值或最大中的最小值，用两段二分
                l = k + 1;
            }else{
                r = k;
            }
        }
        return l;
    }

719. 找出第 K 小的数对距离
数对 (a,b) 由整数 a 和 b 组成，其数对距离定义为 a 和 b 的绝对差值。
给你一个整数数组 nums 和一个整数 k ，数对由 nums[i] 和 nums[j] 组成且满足 0 <= i < j < nums.length 。返回 所有数对距离中 第 k 小的数对距离。

示例 1：
输入：nums = [1,3,1], k = 1
输出：0
解释：数对和对应的距离如下： (1,3) -> 2 (1,1) ->0 (3,1) -> 2 距离第 1 小的数对是 (1,1) ，距离为 0 。

【分析】排序 + 二分查找 + 双指针
先将数组 $\text{nums}$ 从小到大进行排序。因为第 kk 小的数对距离必然在区间 $[0,\max (\text{nums})-\min (\text{nums})]$ 内，令 $\text{left}=0$，$\text{right}=\max (\text{nums})-\min (\text{nums})$，我们在区间 $[\text{left},\text{right}]$ 上进行二分。

对于当前搜索的距离 $\text{mid}$，计算所有距离小于等于 $\text{mid}$ 的数对数目 $\text{cnt}$，如果 $\text{cnt}\ge k$，那么 $\text{right}=\text{mid}-1$，否则 $\text{left}=\text{mid}+1$ 。当 $\text{left}>\text{right}$ 时，终止搜索，那么第 $k$ 小的数对距离为 $\text{left}$。
给定距离 $\text{mid}$，计算所有距离小于等于 $\text{mid}$ 的数对数目 $\text{cnt}$ 可以使用双指针：初始左端点 $i=0$，我们从小到大枚举所有数对的右端点 $j$，移动左端点直到 $\text{nums}[j]-\text{nums}[i]\le \text{mid}$，那么右端点为 $j$ 且距离小于等于 $\text{mid}$ 的数对数目为 $j-i$，计算这些数目之和。

	int smallestDistancePair(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        int l = 0, r = nums[n - 1] - nums[0];
        while(l < r){
            int mid = ((r - l) >> 1) + l;
            int cnt = 0;
            for(int i = 0, j = 0; j < n; ++j){
                while(nums[j] - nums[i] > mid) ++i;
                cnt += j - i;
            }
            if(cnt < k){
                l = mid + 1;
            }else{
                r = mid;
            }
        }
        return l;//等价于 r
    }

还可以用下面的STL库函数实现二分查找：

binary_search(first, last, target)

查找某个元素是否出现，返回1或0
头文件：#include
函数模板：binary_search(arr[],arr[]+size , target)
参数说明：
arr[]： 数组首地址
size：数组元素个数
indx:需要查找的值
函数功能： 在数组中以二分法检索的方式查找，若在数组(要求元素非递减)中查找到target元素则真，若查找不到则返回值为假。

    int a[100]= {4,10,11,30,69,70,96,100};
    int b=binary_search(a,a+9,4);//查找成功，返回1
    cout<<"在数组中查找元素4，结果为："<<b<<endl;
    int c=binary_search(a,a+9,40);//查找失败，返回0

lower_bound(first, last, target, cmp)

返回第一个大于或等于某个元素的位置的迭代器
头文件#include
lower_bound()函数要求数组是有序的，底层基于二分查找，所以复杂度也是O(log n)。
作用：
在first到last中的前闭后开有序区间中进行二分查找，返回大于或等于target的第一个元素位置的迭代器。
如果所有元素都小于target，则返回end()的位置（比如matrix[i].end() ），且end()的位置是越界的！！
通过返回的地址减去起始地址begin（）,可以得到找到数字在数组中的下标。lower_bound前不用加数组名。
第四个参数可以省略，是自己定义的比较函数，比如要查找的不是基本数据类型，而是自己定义的struct时就需要自己定义一下，怎么比较两个struct的大小。表示在 [first, last) 区域内查找第一个不符合 cmp规则的元素。
注意：
1）matrix[0].begin()与matrix[0]不同，对于二维向量，要获取二分查找返回位置的下标，应该再减去matrix[i].begin()
2）如果题目要求查找某个元素，当该元素不存在时也会返回大于该元素的第一个位置迭代器，需要额外加个判断。
样例：

int i =lower_bound(matrix[0].begin(),matrix[0].end(),num)-matrix[0].begin();

或者

vector<int>::iterator it;
it = lower_bound(matrix[0].begin(),matrix[0].end(),num);

因此35. 搜索插入位置可以用一行代码解答：

return lower_bound(nums.begin(),nums.end(),target) - nums.begin();

注意点：
因为 lower_bound 返回的是一个迭代器，所以它要减去nums.begin()这个迭代器得到的差值才是下标的编号。

此外，当集合数据结构 set 调用lower_bound 函数时，需要换一种写法，比如729. 我的日程安排表 I 中查找起点大于等于 end 的第一个区间时，应该像下面这样调用：

	set<pair<int, int>> calendar;
	bool book(int start, int end) {
        //每次查找起点大于等于 end 的第一个区间
        //对于集合set而言没有下面这种用法
        // auto it = lower_bound(calendar.begin(), calendar.end(), {end, 0});
        //集合set需要这样调用二分查找函数
        auto it = calendar.lower_bound({end, 0});
        
        //同时紧挨着这个第一个区间的前一个区间的后端（注意不是前端）需要≤start
        if(it == calendar.begin() || (--it)->second <= start){
            calendar.insert({start, end});
            return true;
        }
        return false;
    }

upper_bound(first, last, target)

返回第一个大于某个元素的位置的迭代器
头文件#include
用法跟lower_bound()一样，只不过它返回的是第一个大于target的值的迭代器， 而lower_bound()是返回第一个大于等于target的值的迭代器，>和 >= 是二者的区别
示例：

#include 
#include 
using namespace std;
int main(int argc, char *argv[]){
    int a[] = {1, 3, 5, 7, 9};
    cout << (lower_bound(a, a + 5, 1) - a) << endl;
    // 第一个大于等于1的元素是1，下标是0
    cout << (lower_bound(a, a + 5, 8) - a) << endl;
    // 第一个大于等于8的元素是9，下标是4
    cout << (lower_bound(a, a + 5, 100) - a) << endl;
    // 最大的元素也不比100大，故返回值是last，再减a也就是5

	cout << (upper_bound(a, a + 5, 1) - a) << endl;
    // 第一个大于1的元素是3，下标是1
    cout << (upper_bound(a, a + 5, 7) - a) << endl;
    // 第一个大于7的元素是9，下标是4
    cout << (upper_bound(a, a + 5, 100) - a) << endl;
    // 最大的元素也不比100大，故返回值是last，再减a也就是5
}

【拓展】
1）查找第一个小于等于x的数（注：这里的意思为小于x的数里最大的那个）
算法：upper_bound()的返回值 - 1，就是要查找的地址
2）查找第一个小于x的数：
算法：lower_bound()的返回值 - 1，就是要查找的地址

【附】关于以上三个函数的简介博客
三个函数的使用对比：

#include
#include
using namespace std;
int main()
{
    int a[100]= {4,10,11,30,69,70,96,100};
    int b=binary_search(a,a+9,4);//查找成功，返回1
    cout<<"在数组中查找元素4，结果为："<<b<<endl;
    int c=binary_search(a,a+9,40);//查找失败，返回0
    cout<<"在数组中查找元素40，结果为："<<c<<endl;
    int d=lower_bound(a,a+9,10)-a;
    cout<<"在数组中查找第一个大于等于10的元素位置，结果为："<<d<<endl;
    int e=lower_bound(a,a+9,101)-a;
    cout<<"在数组中查找第一个大于等于101的元素位置，结果为："<<e<<endl;
    int f=upper_bound(a,a+9,10)-a;
    cout<<"在数组中查找第一个大于10的元素位置，结果为："<<f<<endl;
    int g=upper_bound(a,a+9,101)-a;
    cout<<"在数组中查找第一个大于101的元素位置，结果为："<<g<<endl;
}

【附】LeetCode二分查找相关练习—由简到难
704. 二分查找
35. 搜索插入位置
33. 搜索旋转排序数组
81. 搜索旋转排序数组 II
34. 在排序数组中查找元素的第一个和最后一个位置
74. 搜索二维矩阵
240. 搜索二维矩阵 II
（240题属于特殊情况下的Z字形查找，比二分查找效率更高。二分查找是一次删掉半行或半列，Z字查找是一次删除一行或一列）

排序

sort() 不稳定排序

sort函数的底层实现原理

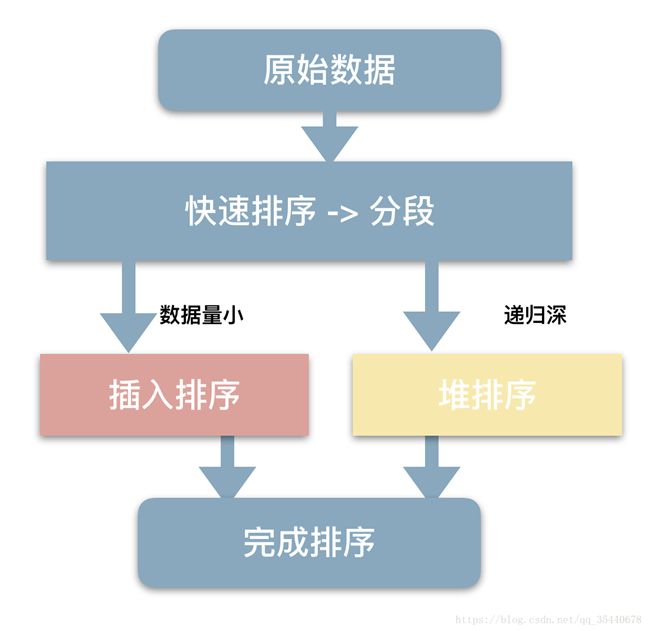
STL中的 sort（begin, end, comp）函数使用的排序方法是类似于快速排序的方法，但又不仅仅是简单的快排，还结合了插入排序和堆排序。总结来说就是sort函数是结合了 快速排序+插入排序+堆排序 这三种排序算法的 综合性STL算法。sort 函数是一类不稳定的排序算法（相同大小元素可能会交换位置）。
STL的sort算法，数据量大时采用QuickSort快排算法，进行分段。一旦分段后的数据量小于某个门槛（16），因为插入排序在面对“几近排序”的序列时，表现更好，同时为了避免QuickSort快排的递归调用带来过大的额外负荷，就改用Insertion Sort插入排序。如果递归层次过深，还会改用HeapSort堆排序。

sort 函数的使用

sort函数可以自定义bool返回值类型比较函数，两个参数先后为a和 b，若返回为true，则表示排序结束后，参数a排在参数b的前面，由于在传参时，两个参数a, b在原数组中排列顺序为先b后a，因此返回为true时，需要进行元素位置交换。（例题：937. 重新排列日志文件）

注意：
1）排序要求容器支持随机访问迭代器，类似于数组的那种下标偏移访问。
2）比较函数必须写在类外部（全局区域）或声明为静态static函数
因为当comp作为类的成员函数时，默认拥有一个this指针，这样和sort函数所需要使用的排序函数类型不一样。否则，会出现 错误
3）比较函数中形参为引用时，需要加const。或者不使用引用类型的形参。下面两种用法都可以。

static bool cmp(const string& log1, const string& log2){ ...}
static bool cmp1( string log1, string log2){..}

对 sort或stable_sort 传定制比较函数的样例：

#include 
typedef struct tagNode {
    int index;
    int value;
} Node;
//const 与 & 搭配使用。在类中定义的比较函数还需要加上static
bool comp(const Node &a, const Node &b){
    return a.value > b.value; //大于号，小顶堆，降序排列
}

int main(){
    vector<Node> a = { {1, 11}, {3, 33}, {2, 22}, {5, 55}, {4, 44} };
    // 编译器会进行类型推导做模板特化 
    sort(a.begin(), a.end(), comp);
    for(auto b : a){
        cout<<b.value<<" "; //降序输出：55 44 33 22 11
    } 
    return 0;
}

总结：
①sort函数根据comp函数的返回值，对comp函数的两个参数排序。
如果comp返回true，排序为“参数1”“参数2”，否则排序为“参数2”“参数1”。
想要升序排列，则return parameter1 < parameter2
想要降序排列，则return parameter1 > parameter2
当比较函数按照参数顺序return时，口诀：
大于号，小顶堆greater()，降序排列； 小于号，默认大顶堆，升序排列。

②comp函数必须写在类外部（全局区域）或声明为静态static函数

③另外，functional提供了一堆基于模板的比较函数对象，分别是：equal_to、not_equal_to、greater、greater_equal、less、less_equal。其中，经常用到的是greater和less。

//vector& nums为形参
sort(nums.begin(), nums.end()); //默认升序
sort(nums.begin(), nums.end(), less<int>()); //默认升序
sort(nums.begin(), nums.end(), greater<int>());  //降序
sort(nums.begin(), nums.end(), comp); //自定义bool返回值类型比较函数
bool comp(int a, int b){
return a>b; //降序排列
}
//若在类内定义，需要加static声明
static bool comp(int a, int b) {...}

此外，comp比较函数也可以写为lambda表达式的形式，C++ 11 中的 Lambda 表达式用于定义并创建匿名的函数对象，以简化编程工作。Lambda 的语法形式如下：

[捕获列表] (函数参数) mutable/exception/attribute 函数声明选项 -> 返回值类型 {函数体}

如435. 无重叠区间中的sort 函数可以这样写：

vector<vector<int> > intervals;
sort(intervals.begin(),intervals.end(),[](const auto &u,const auto &v){return u[1]<v[1];});//区间[[1,2],[2,3],[3,4],[1,3]]按右端从小到大排序

stable_sort() 稳定排序

stable_sort用的是归并排序的思路，刚好解决了sort排序不稳定的缺点。平均情况下，快速排序和归并排序复杂度都是O(nlogn)。

不仅有sort和stable_sort，还有 partition 和stable_partition，带有stable的函数可保证相等元素的原本相对次序在排序后保持不变。

stable_sort() 函数完全可以看作是 sort() 函数在功能方面的升级版。换句话说，stable_sort() 和 sort() 具有相同的使用场景，就连语法格式也是相同的，只不过前者在功能上除了可以实现排序，还可以保证不改变相等元素的相对位置。

例题：937. 重新排列日志文件
题目见链接，题解如下：
考察点： comp函数参数是否加const ； comp函数是否加static ；comp函数返回值为false时不交换元素，排序后第二个参数排在第一个参数的前面（对应原数组中位置，第二个参数原本在第一个参数的后面），也就是不交换元素顺序，按照原数组顺序即可 ； find函数 ；substr 函数 ； isdigit函数

	static bool comp(const string& log1, const string& log2){ 
	//注意cosnt string& 或者string
        int pos1 = log1.find(" ");
        int pos2 = log2.find(" ");
        bool isdigit1 = isdigit(log1[pos1+1]);
        bool isdigit2 = isdigit(log2[pos2+1]);
        if(isdigit1 && isdigit2){
            return false;  //返回值为false为不交换元素位置，为true时交换
        }
        if(!isdigit1 && !isdigit2){
            string str1 = log1.substr(pos1+1);
            string str2 = log2.substr(pos2+1);
            if(str1 != str2){
                return str1 < str2;
            }else{
                return log1 < log2;
            }
        }
        return isdigit1? false:true;
    }

    vector<string> reorderLogFiles(vector<string>& logs) {
        stable_sort(logs.begin(), logs.end(), comp);
        return logs;
    }

常用排序算法

常用的排序算法（按排序依据原则）：
最好的排序算法为$O(nlogn)$，最差为 $O(n^2)$

1.插入排序：
每次将一个待排序的记录，按关键字的大小插入到已排好序的子序列中的适当位置，直到全部记录插入完毕为止。
（1）直接插入排序 $O(n^2)$
（2）希尔排序，较小的$O(n^2)$
先隔几个进行直接插入排序，分割成若干子序列，使得整个序列“基本有序”，再对全体记录进行一次直接插入排序。

2.交换排序：
两两比较待排序记录的关键值，交换不满足顺序要求的记录，直到全部满足顺序要求为止。
（1）冒泡排序 $O(n^2)$
（2）快速排序
最差情况每次都选到最小元素作为枢轴，$O(n^2)$
最好情况，每次总选到中间值作枢轴 $O(nlogn)$

3.选择排序
每次从待排序记录中选出关键字最小的记录，顺序放在已排序的记录序列的后面，直到全部排完。
（1）简单选择排序 $O(n^2)$
（2）堆排序 $O(nlogn)$

4.基数排序：$O(d(n+rd))$
多关键字排序方法。

5.归并排序 $O(nlogn)$
先相邻两两一组合并排序，再两两合并排序，直到得到一个有序序列为止

快速排序

题目练习： 912. 排序数组 与 215. 数组中的第K个最大元素
注意点：
1）内部while循环时也要注意先保证left，否则可能会造成数组越界
2）这两块函数形参类型相同，quickSort返回值为int，用于每次至少将传入数组中的最左侧元素temp排好位置，并且返回其下标k。
排序时最好情况是每次选择的最左元素temp为中间值大小，这样每次可以最大程度减少交换移动次数，达到$O(nlogn)$。
3）quick函数无返回值，其中的判断函数要用if，若用while会陷入重复排同一块数组的死循环。
首先通过quickSort得到排好序的那个元素的下标K,然后将数组分治为两部分较小的数组，并递归调用quick函数自身，继续递归分治数组，直到单个元素都排好序。
这里也体现出如果每次选择排序的元素都是中间值，那么数组可以均分平分，这样处理起来也会加快，达到$O(nlogn)$

下面代码是优化后的基于随机选取主元的快速排序，时间复杂度为期望$O(nlogn)$

//注意快速排序经常会出现的一些问题
//每次排好一个元素temp
    int partition(vector<int>& nums, int l, int r){
        int temp = nums[l];
        //相等时退出循环
        while(l < r) {
        	//注意保证left < right
            while(l < r && nums[r] >= temp){
                --r;
            }
            nums[l] = nums[r]; 
            //注意保证left
            while(l < r && nums[l] <= temp){
                ++l;
            }
            nums[r] = nums[l];        
        }
        nums[l] = temp;//最后别忘了赋值回来
        return l;
    }
    //随机选择要排序的主元，增加随机性，是优化部分
     int randomized_partition(vector<int>& nums, int l, int r){
        int i = rand() % (r - l + 1) + l;// 随机选一个作为我们的主元（分界值）
        swap(nums[l], nums[i]);
        return partition(nums, l, r);
    }
    void quickSort(vector<int>& nums, int l, int r){
        //注意：不是while
        if(l < r) {
            int k = randomized_partition(nums, l, r);//此处采用随机方式选择主元
            quickSort(nums, l, k-1);//left不加1
            quickSort(nums, k+1, r);//此处递归
        }        
    }
    //调用优化后的快速排序算法
    vector<int> sortArray(vector<int>& nums) {
    //在rand()生成随机数之前设置一次随机种子，采用系统时间来初始化
    //srand(time(0));//(unsigned)
        srand((unsigned)time(NULL)); 
        quickSort(nums, 0, (int)nums.size() - 1);
        return nums;
    }

当然，简单一点也可以用sort函数一句话排序解决。
215. 数组中的第K个最大元素
在上面基础上修改的部分：

	int quicksort(vector<int>& nums, int l, int r, int k){
        //if(l < r){
            int m = random(nums, l, r);
            if(m == k) return nums[m];
            return m > k ? quicksort(nums, l, m - 1, k) : quicksort(nums, m + 1, r, k);
        //} 当 l >= r 时没有返回值类型了，因此需要注释掉
    }
    int findKthLargest(vector<int>& nums, int k) {
        srand(time(0));//(unsigned)       
        return quicksort(nums, 0, nums.size() - 1, nums.size() - k); //nums.size() - k
    }

堆排序

堆排序： 堆是一种特殊的树形数据结构，即完全二叉树。堆分为大根堆和小根堆，大根堆为根节点的值大于两个子节点的值；小根堆为根节点的值小于两个子节点的值，同时根节点的两个子树也分别是一个堆。
通常用的都是大顶推，大顶堆是小于号，每次选出最大值放到数组末尾，排序完之后的数组是升序序列。排序或优先级队列默认大顶堆less (); greater是小顶堆。
题目练习：215. 数组中的第K个最大元素 与 912. 排序数组

调整大顶堆adjust与堆排序heapSort的基本思路：
（注：下面这三个加粗的关键步骤都是heapSort函数的主步骤，该函数依赖于从上到下调整大顶堆的adjust函数的实现）
步骤一：建立大根堆
—将n个元素组成的无序序列构建一个大根堆
① 默认为原无序数组本身就是一个虚拟的已经建立好的完全二叉树。
② 从最后一个叶子节点（N/2-1）开始，从左到右，从下到上调用调整函数adjust，将完全二叉树调整为大根堆
步骤二：交换堆元素
—交换堆尾元素和堆首元素，使堆尾元素为最大元素；
步骤三：重建大根堆
—将前n-1个元素组成的无序序列调整为大根堆
重复执行步骤二和步骤三，直到整个序列有序。

#include
#include
using namespace std;
//建大顶堆，并从当前结点开始往下调整左右子树为大顶堆
//必须要有传入数组长度的size参数，因为要不断调整将最大值置后的，长度减一后剩下的数组为大顶堆
    void adjust(vector<int>& nums, int size, int index) {
        int maxid = index;
        int l = 2*index+1;  //左孩子
        int r = 2*index+2;  //右孩子
        //l
        if(l < size && nums[l] > nums[maxid]) maxid = l;
        if(r < size && nums[r] > nums[maxid]) maxid = r;
        //不能用while，会陷入死循环
        if(maxid != index){
            //交换了序号对应的数值，但是序号没有交换
            swap(nums[maxid], nums[index]);
            //交换之后可以保证当前这个顶部的index结点位置为最大
            //但是左右孩子对应的maxid子树不一定是大顶堆，需要递归调整index结点下面的孩子为大顶堆
            adjust(nums, size, maxid);
        }
    }
    void heapSort(vector<int>& nums){
        int n = nums.size();
        int index = n/2-1;  //找到第一个非叶子节点
        //从第一个非叶子结点向上开始调整建立大顶堆，默认原数组就是已经建立好的堆
        for(int i = index; i >= 0; --i){
            adjust(nums, n, i);
        }
        //建完大顶堆之后依次将堆顶最大值移至数组末尾，重新调整剩下长度的元素为大顶堆
        for(int i = n - 1; i >= 1; --i){
            // 将当前最大值放置到数组末尾
            swap(nums[0], nums[i]);
            // 将未完成排序的剩余部分继续进行堆排序
            //可以看到adjust函数若没有数组长度这一参数，就会陷入不断调整整个nums原数组的死循环了，
            //所以应该让该函数增加长度参数限制，并每次只调整长度不断缩减的剩余数组堆
            adjust(nums, i, 0);
        }
    }
    int main(){
    vector<int> arr = {3, 2, 1, 5, 6, 4};
    heapSort(arr);
    for(int i=0; i<arr.size(); i++){
        cout<<arr[i]<<endl; //输出 1 2 3 4 5 6 
    }
    return 0;
}

注意点：
1）adjust()与heapSort()函数的返回值都是void类型，adjust()作为从上到下调整大顶堆的函数，必须要有数组长度的参数作为一种调整限制。
2）从第一个非叶子结点（N/2-1）向上开始调整建立大顶堆，默认原数组就是已经建立好的堆。
3）建完大顶堆之后依次将堆顶最大值移至数组末尾，重新调整剩下长度的元素为大顶堆。

归并排序

思路：
归并排序利用了分治的思想来对序列进行排序。对一个长为 n 的待排序的序列，我们将其分解成两个长度为 $n/2$的子序列。每次先递归调用函数使两个子序列有序，然后我们再线性合并两个有序的子序列使整个序列有序。

算法：
定义 mergeSort(nums, l, r) 函数表示对 nums 数组里 [l,r]的部分进行排序，整个函数流程如下：
1.递归调用函数 mergeSort(nums, l, mid) 对 nums 数组里 [l,r] 部分进行排序。
2.递归调用函数 mergeSort(nums, mid + 1, r) 对 nums 数组里 [mid+1,r] 部分进行排序。
3.此时 nums 数组里 [l,mid] 和 [mid+1,r] 两个区间已经有序，我们对两个有序区间线性归并即可使 nums 数组里 [l,r] 的部分有序。

线性归并的过程并不难理解，由于两个区间均有序，所以我们维护两个指针 i 和 j 表示当前考虑到 [l,mid] 里的第 i 个位置和 [mid+1,r] 的第 j 个位置。

如果 nums[i] <= nums[j] ，那么我们就将nums[i] 放入临时数组 tmp 中并让 i += 1 ，即指针往后移。否则我们就将nums[j] 放入临时数组 tmp 中并让 j += 1 。如果有一个指针已经移到了区间的末尾，那么就把另一个区间里的数按顺序加入 tmp 数组中即可。

这样能保证我们每次都是让两个区间中较小的数加入临时数组里，那么整个归并过程结束后 [l,r] 即为有序的。

题目练习：215. 数组中的第K个最大元素 与 912. 排序数组

    vector<int> temp;
    void mergeSort(vector<int>& nums, int l, int r){
        if(l >= r) return;
        int mid = (r + l) >> 1;
        mergeSort(nums, l, mid);
        mergeSort(nums, mid + 1, r);
        int i = l, j = mid + 1, k = 0;
        while(i <= mid && j <= r){
            if(nums[i] <= nums[j]){
                temp[k++] = nums[i++];
            }
            else{
                temp[k++] = nums[j++];
            }
        }
        while(i <= mid) temp[k++] = nums[i++];
        while(j <= r) temp[k++] = nums[j++];
        for(int n = 0; n < r - l + 1; ++n){
            nums[n + l] = temp[n];
        }
    }
    vector<int> sortArray(vector<int>& nums) {
        temp.resize(nums.size()); //重置容量容易遗漏
        mergeSort(nums, 0, nums.size() - 1);
        return nums;
    }

[补充]
resize()，设置大小;
reserve()，设置容量;
resize()是分配容器的内存大小，而reserve()只是设置容器容量大小，但并没有真正分配内存。
resize()可以传递两个参数，分别是大小和初始值，初始值默认为0，reserve()只能传递一个参数，不能设置初始值，其初始值为系统随机生成。

链表归并排序

可以对照着数组的归并排序来看
148. 排序链表
给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

示例1：

输入：head = [4,2,1,3]
输出：[1,2,3,4]

【思路】时间复杂度是 $O(n\log n)$ 的排序算法包括归并排序、堆排序和快速排序（快速排序的最差时间复杂度是 $O(n^2)$，其中最适合链表的排序算法是归并排序。归并排序基于分治算法。最容易想到的实现方式是自顶向下的递归实现，考虑到递归调用的栈空间，自顶向下归并排序的空间复杂度是 $O(\log n)$,其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间。

对链表自顶向下归并排序的过程如下：
1)找到链表的中点，以中点为分界，将链表拆分成两个子链表。寻找链表的中点可以使用快慢指针的做法，快指针每次移动 2 步，慢指针每次移动 1 步，当快指针到达链表末尾时，慢指针指向的链表节点即为链表的中点。
2)对两个子链表分别排序。
3)将两个排序后的子链表合并，得到完整的排序后的链表。可以使用「21. 合并两个有序链表」的做法，将两个有序的子链表进行合并。

上述过程可以通过递归实现。递归的终止条件是链表的节点个数小于或等于 1，即当链表为空或者链表只包含 1 个节点时，不需要对链表进行拆分和排序。

	//对链表自顶向下归并排序:
    ListNode* mergeSort(ListNode* head, ListNode* tail){
        //递归的终止条件是链表的节点个数小于或等于 1
        //链表为空
        if(head == nullptr){
            return head;
        }
        //链表只包含 1 个节点
        if(head == tail){ //仅有1个节点时，需要从链表中分离开，将后继节点置为空指针
            head->next = nullptr;
            return head;
        }
        
        //快慢指针找到链表的中点mid，以中点为分界，将链表拆分成两个子链表。
        ListNode* fast = head, *slow = head;
        while(fast != tail){ //注意不是fast != nullptr，中间断开，所以结尾不一定为空            
            fast = fast->next;
            if(fast != tail){               
                fast = fast->next;
                slow = slow->next;
            }
        } 
        ListNode* mid = slow;

        //对两个子链表分别排序。       
        ListNode* p2 = mergeSort(mid->next, tail); 
        //注意！！！！特别易错点
        //下面的语句在单节点时候，head == tail，将head与tail的next置为nullptr之后
        //mid->next会变为空，因此需要将这两句更换一下顺序，否则传入空指针mid->next报错
        ListNode* p1 = mergeSort(head, mid);
        
        //使用「21. 合并两个有序链表」的做法，将两个有序的子链表进行合并。
        ListNode* dummyHead = new ListNode();
        ListNode* cur = dummyHead;
        while(p1  && p2 ){
            if(p1->val <= p2->val){
                cur->next = p1;
                p1 = p1->next;
            }else{
                cur->next = p2;
                p2 = p2->next;
            }
            cur = cur->next;
        }
        if(p1) cur->next = p1; //注意不是while
        if(p2) cur->next = p2; //不是while
        return dummyHead->next;
    }
    //调用归并排序
    ListNode* sortList(ListNode* head) {
        return mergeSort(head, nullptr);
    }

在前半部分还可以像下面这样写，采取左闭右开区间 [ head, tail )，当仅剩两个节点时，将head的next置为空指针，从中间断开，相当于将tail覆盖住，这样可以避免出现递归中 mid->next 被置为空而又要调用 mid->next 的问题。
这样可以将链表一分为二，并且两部分的首尾重叠，每个单节点部分的尾部都会被覆盖掉，这样最后两两归并时候的节点不会重复也不会少。

	ListNode* mergeSort(ListNode* head, ListNode* tail){
        //链表为空
        if(head == nullptr){
            return head;
        }
        //链表只包含 1 个节点
        //左闭右开区间，仅有两个节点时，将右节点用空指针覆盖掉（其实只是从中间断开）
        if(head->next == tail){ 
            head->next = nullptr;
            return head;
        }
        //快慢指针找到链表的中点mid，以中点为分界，将链表拆分成两个子链表。
        同上
        
        //对两个子链表分别排序。
        ListNode* p1 = mergeSort(head, mid);  
        //mid->next可能为 nullptr，因此不能用mid->next,采取左闭右开区间     
        ListNode* p2 = mergeSort(mid, tail); 
        
        //使用「21. 合并两个有序链表」的做法，将两个有序的子链表进行合并。
         同上
         //调用归并排序 
         同上

【升级版】23. 合并K个升序链表
给你一个链表数组，每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：
输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
1->4->5,
1->3->4,
2->6
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

【思路】可以利用链表归并的方式进行两两归并，本题采用优先级队列的方法。
使用优先队列合并
需要维护当前每个链表没有被合并的元素的最前面一个，k 个链表就最多有 k 个满足这样条件的元素，每次在这些元素里面选取 $\text{val}$ 属性最小的元素合并到答案中。在选取最小元素的时候，我们可以用优先队列来优化这个过程。
【注意点】
1.优先级队列数据类型为结构体时，可以在结构体内重载<运算符，让系统知道如何判断两个结构体的大小关系，便可以调用优先级队列中默认的大顶堆了。否则就需要自己写一个仿函数。
2.可以用 {一一对应的结构体的每个数据成员，逗号间隔} 表示结构体，比如下面的样例：
3.结构体用 . 运算符，指针用 -> 运算符，容易搞混

struct node{
    int val;
    int age;
    int name;
    bool operator<(const node cur) const{
        return val > cur.val;
    }
};
priority_queue<node> q;
int main(){
    q.push({6, 2, 3}); //分别对应val=6, age =2, name = 3
    q.push({1, 3, 7});
    cout<<q.top().val<<endl; //输出 1， 说明队顶结构体为｛1，3，7｝
    return 0;
}

本题的代码如下：

	struct Node{
        int val;
        ListNode* ptr;
        //重载<运算符
        bool operator<(const Node &cur) const{
            return val > cur.val;
        }
    };

    priority_queue<Node> q;

    ListNode* mergeKLists(vector<ListNode*>& lists) { 
        //当头结点不为空时，将每个链表的头结点存入队列
        //注意判断头结点是否为空，
        //注意结构体的传入形式，可以用{结构体的每个数据成员，逗号间隔}表示结构体       
        for(auto &lst : lists){
            if(lst) q.push({lst->val, lst});
        }
        ListNode *head = new ListNode();
        ListNode* cur = head;
        while(!q.empty()){
            cur->next = q.top().ptr; //结构体用. 不用->
            cur = cur->next;
            if(cur->next){
                q.push({cur->next->val, cur->next});
            }
            q.pop();
        }
        return head->next;
    }

哈希表自定义排序

如何利用unordered_map + 自定义排序？
这里需要用到pair

unordered_map<int, int> ht;
// 转为pair以对value进行排序
vector<pair<int, int>> tmp;
        for(auto it = ht.begin(); it!=ht.end(); it++)
{
            tmp.push_back(pair<int, int>(it->first, it->second));
        }
// 降序排序
static bool cmp(pair<int, int> a, pair<int, int> b)
{
        return a.second > b.second;
}
sort(tmp.begin(), tmp.end(), cmp);