湖南科技大学计算智能课设（二）以人事招聘为例的误差反向传播算法

以人事招聘为例的误差反向传播算法

写在前面

这篇文章是课设的相关记录，有些地方可能会写的不对，欢迎大家指正。如果我有哪里写的不清楚也可以私信与我沟通，各位写课设的学弟学妹加油～

实验目的

理解多层神经网络的结构和原理，掌握反向传播算法对神经元的训练过程，了解反向传播公式。通过构建 BP 网络实例，熟悉前馈网络的原理及结构。

背景知识

误差反向传播算法即 BP 算法，是一种适合于多层神经网络的学习算法。其建立在梯度下降方法的基础之上，主要由激励传播和权重更新两个环节组成，经过反复迭代更新、修正权值从而输出预期的结果。
BP 算法整体上可以分成正向传播和反向传播，原理如下:
正向传播过程：信息经过输入层到达隐含层，再经过多个隐含层的处理后到达输出层。
反向传播过程：比较输出结果和正确结果，将误差作为一个目标函数进行反向传播
对每一层依次求对权值的偏导数，构成目标函数对权值的梯度，网络权重再依次完成更新调整。 依此往复、直到输出达到目标值完成训练。
该算法可以总结为：利用输出误差推算前一层的误差，再用推算误差算出更前一层的误差，直到 计算出所有层的误差估计。
1986 年，Hinton在论文《Learning Representations by Back-propagating Errors》中首次系统地描述了如何利用 BP 算法来训练神经网络。
从此，BP 算法开始占据有监督神经网络算法的核心地位。它是迄今最成功的神经网络学习算法之一，现实任务中使用神经网络时，大多是在使用 BP 算法进行训练。
为了说明 BP 算法的过程，本实验使用一个公司招聘的例子：假设有一个公司，其人员招聘由 5 个人组成的人事管理部门负责，如下图所示：
其中张三、李四等人是应聘者，他们向该部门投递简历，简历包括两类数据：学习成绩和社会实践得分，人事部门有三个层级，一科长根据应聘者的学习成绩和实践得分评估其智商，二科长根据同样的资料评估其情商；一处长根据两个科长提供的智商、情商评分，评估应聘者的工作能力，二处长评估工作态度；最后由总裁汇总两位处长的意见，得出最终结论，即是否招收该应聘者。
该模型等价于一个形状为(2,2,2,1)的前馈神经网络，输入层、隐藏层 1、隐藏层 2、输出层各自包含 2、2、2、1 个节点，如下图所示。
除输入节点外，每个节点都执行汇总和激活两个操作。汇总得到的数值称为净输入，用字母 $\mathbf{z}$ 表示。激活采用 sigmoid 函数，激活后的数据称为该节点的输出，用字母 $\mathbf{a}$ 表示。字母的上标代表该节点位于哪一层，下标代表该节点是该层第几个节点。注意输入节点位于 0 层。
节点与节点之间边的权值用字母 $\mathbf{w}$ 表示，上标代表该权值属于哪一层，下标有两个，代表其连接的是左侧(上一层)第几个节点到右侧(下一层)第几个节点。偏置用字母 $\mathbf{b}$ 表示，它可以视为输入恒为 1 的边的权值。
为所有 $\mathbf{w}$ 和 $\mathbf{b}$ 赋初值，针对一个样本或多个样本从左到右计算出所有 $\mathbf{z}$ 和 $\mathbf{a}$ 的过程，即正向传播。 经正向传播后，神经网络的最终输出，记为 $\hat{\mathbf{y}}$。在本案例中，$\hat{\mathbf{y}}={\mathbf{a}}_1^3$。
通过设计一个由权值和偏置决定的目标函数 $\mathbf{J}(\mathbf{W},\mathbf{b})$ ，可以求出目标函数对 $\hat{\mathbf{y}}$ 的偏导数 $\frac{\partial \mathbf{J}(\mathbf{W},\mathbf{b})}{\partial \hat{\mathbf{y}}}=\frac{\partial \mathbf{J}(\mathbf{W},\mathbf{b})}{\partial {\mathbf{a}}_1^3}$ (目标函数并不一定包含$\hat{\mathbf{y}}$ ，但本案例只讨论这种常见的情况)，将该偏导数看成由权值和偏置导致的误差，一层一层将误差反向传导到所有的权值和偏置，就是反向传播过程。
实际编程时进行了向量化(Vectorization)，即将对标量的多次循环计算，用对向量、矩阵、 张量的一次运算来替代，见下图。应聘者的输入被组织为向量 $\mathbf{A}0$，第一层的 4 个权值被组织为矩阵 $\mathbf{W}1$， 隐藏层 1 节点的汇总结果被组织为向量 $\mathbf{Z}1$，对应的输出被组织为 $\mathbf{A}1$。其它层类似。最后的 $\mathbf{Z}3$ 和 $\mathbf{A}3$ 在本例中是标量。

必须指出，为方便理解，本招聘案例在一开始就定义了隐藏层结点的作用：评估应聘者的智商、 情商、工作能力、工作态度等特征。但神经网络的特点是自动进行特征工程，隐藏层结点自主学习、 自动提取输入数据的特征，最后形成的决策权值，并不一定代表智商、情商、工作能力、工作态度。

完整代码及注释讲解

import numpy as np
import matplotlib.pyplot as plt

# 输入数据1行2列，这里只有张三的数据
X = np.array([[1,0.1]])
# X = np.array([[1,0.1],
#               [0.1,1],
#               [0.1,0.1],
#               [1,1]])
# 标签，也叫真值，1行1列，张三的真值：一定录用
T = np.array([[1]])
# T = np.array([[1],
#               [0],
#               [0],
#               [1]])

# 定义一个2隐层的神经网络：2-2-2-1
# 输入层2个神经元，隐藏1层2个神经元，隐藏2层2个神经元，输出层1个神经元

# 输入层到隐藏层1的权值初始化，2行2列
W1 = np.array([[0.8,0.2],
              [0.2,0.8]])
# 隐藏层1到隐藏层2的权值初始化，2行2列
W2 = np.array([[0.5,0.0],
              [0.5,1.0]])
# 隐藏层2到输出层的权值初始化，2行1列
W3 = np.array([[0.5],
              [0.5]])


# 初始化偏置值
# 隐藏层1的2个神经元偏置
b1 = np.array([[-1,0.3]])
# 隐藏层2的2个神经元偏置
b2 = np.array([[0.1,-0.1]])
# 输出层的1个神经元偏置
b3 = np.array([[-0.6]])
# 学习率设置
lr = 0.1
# 定义训练周期数10000
epochs = 10000
# 每训练1000次计算一次loss值  # 定义测试周期数
report = 1000
# 将所有样本分组，每组大小为
batch_size = 1

# 定义sigmoid函数
def sigmoid(x):
    return 1/(1+np.exp(-x))

# 定义sigmoid函数导数
def dsigmoid(x):
    return x*(1-x)

# 更新权值和偏置值
def update():
    global batch_X,batch_T,W1,W2,W3,lr,b1,b2,b3
    
    # 隐藏层1输出
    Z1 = np.dot(batch_X,W1) + b1    
    A1 = sigmoid(Z1)

    # 隐藏层2输出
    Z2 = (np.dot(A1,W2) + b2)
    A2 = sigmoid(Z2)
    
    # 输出层输出
    Z3=(np.dot(A2,W3) + b3)
    A3 = sigmoid(Z3)
    
    # 求输出层的误差
    delta_A3 = (batch_T - A3)  # J对A3的偏导（这里已经将梯度转换为负梯度）
    delta_Z3 = delta_A3 * dsigmoid(A3)  # J对Z3的偏导
    
    # 利用输出层的误差，求出三个偏导（即隐藏层2到输出层的权值改变）    
    # 由于一次计算了多个样本，所以需要求平均
    delta_W3 = A2.T.dot(delta_Z3) / batch_X.shape[0]
    delta_B3 = np.sum(delta_Z3, axis=0) / batch_X.shape[0]
    
    # 求隐藏层2的误差
    delta_A2 = delta_Z3.dot(W3.T)  #J对A2的偏导，上一个房间的海水*W3
    delta_Z2 = delta_A2 * dsigmoid(A2)  #J对Z2的偏导，上一个房间的海水*A2*（1-A2）
    
    # 利用隐藏层2的误差，求出三个偏导（即隐藏层1到隐藏层2的权值改变）  
    # 由于一次计算了多个样本，所以需要求平均
    delta_W2 = A1.T.dot(delta_Z2) / batch_X.shape[0]  #J对W2的偏导，上一个房间的海水*A1
    delta_B2 = np.sum(delta_Z2, axis=0) / batch_X.shape[0]  #J对B2的偏导，上一个房间的海水*1
    
    # 求隐藏层1的误差
    delta_A1 = delta_Z2.dot(W2.T)  #J对A1的偏导，上一个房间的海水*W2
    delta_Z1 = delta_A1 * dsigmoid(A1)  #J对Z1的偏导，上一个房间的海水*A1*（1-A1）
    
    # 利用隐藏层1的误差，求出三个偏导（即输入层到隐藏层1的权值改变）   
    # 由于一次计算了多个样本，所以需要求平均
    delta_W1 = batch_X.T.dot(delta_Z1) / batch_X.shape[0]  #J对W1的偏导，上一个房间的海水*输入
    delta_B1 = np.sum(delta_Z1, axis=0) / batch_X.shape[0]  #J对B1的偏导，上一个房间的海水*1
    
    # 更新权值（学习率*负梯度）
    W3 = W3 + lr *delta_W3
    W2 = W2 + lr *delta_W2
    W1 = W1 + lr *delta_W1
    
    # 改变偏置值
    b3 = b3 + lr * delta_B3
    b2 = b2 + lr * delta_B2
    b1 = b1 + lr * delta_B1

# 定义空list用于保存loss
loss = []
batch_X = []
batch_T = []
max_batch = X.shape[0] // batch_size
# 训练模型
for idx_epoch in range(epochs):
    
    for idx_batch in range(max_batch):
        # 更新权值
        batch_X = X[idx_batch*batch_size:(idx_batch+1)*batch_size, :]
        batch_T = T[idx_batch*batch_size:(idx_batch+1)*batch_size, :]
        update()
    # 每训练5000次计算一次loss值
    if idx_epoch % report == 0:
        # 隐藏层1输出
        A1 = sigmoid(np.dot(X,W1) + b1)
        # 隐藏层2输出
        A2 = sigmoid(np.dot(A1,W2) + b2)
        # 输出层输出
        A3 = sigmoid(np.dot(A2,W3) + b3)
        # 计算loss值
        print('A3:',A3)
        print('epochs:',idx_epoch,'loss:',np.mean(np.square(T - A3) / 2))
        # 保存loss值
        loss.append(np.mean(np.square(T - A3) / 2))

# 画图训练周期数与loss的关系图
plt.plot(range(0,epochs,report),loss)
plt.xlabel('epochs')
plt.ylabel('loss')
plt.show()
        
# 隐藏层1输出
A1 = sigmoid(np.dot(X,W1) + b1)
# 隐藏层2输出
A2 = sigmoid(np.dot(A1,W2) + b2)
# 输出层输出
A3 = sigmoid(np.dot(A2,W3) + b3)
print('output:')
print(A3)

# 因为最终的分类只有0和1，所以我们可以把大于等于0.5的值归为1类，小于0.5的值归为0类
def predict(x):
    if x>=0.5:
        return 1
    else:
        return 0

# map会根据提供的函数对指定序列做映射
# 相当于依次把A3中的值放到predict函数中计算
# 然后打印出结果
print('predict:')
for i in map(predict,A3):
    print(i)

实验内容

1）如果去掉总裁这一层，相应张三的样本修改为(1.0,0.1,1.0,1.0)，分别对应张三的学习成绩、张三的实践成绩、张三的工作能力真值、张三的工作态度真值，代码应该如何修改?

修改思路：
将原程序的最后一层取消掉，A2 作为最后输出，A1 作为隐藏层的输出。
将本文上面的原代码的第10-37行修改为：

# 标签，也叫真值，1 行 2 列(将真值改为两个数) 
T = np.array([[1, 1]])

# 原程序：
# 定义一个 2 隐层的神经网络：2-2-2-1
# 输入层 2 个神经元，隐藏 1 层 2 个神经元，隐藏 2 层 2 个神经元，输出层 1 个神经元
# 题目一：
# 定义一个 1 隐层的神经网络：2-2-2
# 输入层 2 个神经元，隐藏层 2 个神经元，输出层 2 个神经元

# 输入层到隐藏层的权值初始化，2 行 2 列，同一行是从同一个节点发出的权值
# (只有一个隐藏层，W1 作为输入层到隐藏层之间的权值)
W1 = np.array([[0.8, 0.2],
              [0.2, 0.8]])
              
# 隐藏层到输出层的权值初始化，2 行 2 列 
W2 = np.array([[0.5,0.0],
              [0.5,1.0]])
              
# 原程序这段注释掉
# 隐藏层 2 到输出层的权值初始化，2 行 1 列
# W3 = np.array([[0.5], 
#                [0.5]])

# 初始化偏置值
# 隐藏层 1 的 2 个神经元偏置
b1 = np.array([[-1],
              [0.3]])
              
# 原程序：
# 隐藏层 2 的 2 个神经元偏置
# 题目一：
# 输出层的 2 个神经元偏置
b2 = np.array([[0.1],
              [-0.1]])
              
# 原程序这段也注释掉 
# 输出层的 1 个神经元偏置
# b3 = np.array([[-0.6]])

将本文上面的原代码的第67-106行修改为：

# 原程序这段也注释掉
# 输出层输出
# Z3=(np.dot(A2, W3) + b3) 
# A3 = sigmoid(Z3)

# 求输出层的误差
# 原程序：
# delta_A3 = (batch_T - A3) # J对A3的偏导（这里已经将梯度转换为负梯度）
# delta_Z3 = delta_A3 * dsigmoid(A3) # J对Z3的偏导
# 题目一：
delta_A2 = (batch_T - A2) # J 对 A2 的偏导(这里已经将梯度转换为负梯度) 
delta_Z2 = delta_A2 * dsigmoid(A2) # J 对 Z2 的偏导

# 原程序：
# 利用输出层的误差，求出偏导（即隐藏层 2 到输出层的权值改变）
# 由于一次计算了多个样本，所以需要求平均
# delta_W3 = delta_Z3.dot(A2.T) / batch_X.shape[1] #J对W3的偏导，上一个房间的海水*A2
# delta_B3 = np.sum(delta_Z3, axis=1) / batch_X.shape[1] #J对B3的偏导，上一个房间的海水*1
# 题目一：
# 利用输出层的误差，求出偏导(即隐藏层到输出层的权值改变)
# 由于一次计算了多个样本，所以需要求平均
delta_W2 = A1.T.dot(delta_Z2) / batch_X.shape[0] #J 对 W2 的偏导，上一个房间的海水*A1
delta_B2 = np.sum(delta_Z2, axis=0) / batch_X.shape[0] #J 对 B2 的偏导，上一个房间的海水*1

# 原程序：
# 求隐藏层 2 的误差
# delta_A2 = W3.T.dot(delta_Z3) #J对A2的偏导，上一个房间的海水*W3
# delta_Z2 = delta_A2 * dsigmoid(A2) #J对Z2的偏导，上一个房间的海水*A2*（1-A2）
# 题目一：
# 求隐藏层的误差
delta_A1 = delta_Z2.dot(W2.T) #J 对 A1 的偏导，上一个房间的海水*W2
delta_Z1 = delta_A1 * dsigmoid(A1) #J 对 Z1 的偏导，上一个房间的海水*A1*(1-A1)

# 原程序：
# 利用隐藏层 2 的误差，求出偏导（即隐藏层 1 到隐藏层 2 的权值改变）
# 由于一次计算了多个样本，所以需要求平均
# delta_W2 = delta_Z2.dot(A1.T) / batch_X.shape[1] #J对W2的偏导，上一个房间的海水*A1
# delta_B2 = np.sum(delta_Z2, axis=1) / batch_X.shape[1] #J对B2的偏导，上一个房间的海水*1
# 题目一：
# 利用隐藏层的误差，求出偏导(即输入层到隐藏层的权值改变)
# 由于一次计算了多个样本，所以需要求平均
delta_W1 = batch_X.T.dot(delta_Z1) / batch_X.shape[0] # J 对 W1 的偏导，上一个房间的海水*输入 
delta_B1 = np.sum(delta_Z1, axis=0) / batch_X.shape[0] # J 对 B1 的偏导，上一个房间的海水*1

# 原程序这两段注释掉
# 求隐藏层 1 的误差
# delta_A1 = delta_Z2.dot(W2.T) #J 对 A1 的偏导，上一个房间的海水*W2
# delta_Z1 = delta_A1 * dsigmoid(A1) #J 对 Z1 的偏导，上一个房间的海水*A1*(1-A1)

# 利用隐藏层 1 的误差，求出偏导(即输入层到隐藏层 1 的权值改变)
# 由于一次计算了多个样本，所以需要求平均
# delta_W1 = batch_X.T.dot(delta_Z1) / batch_X.shape[0] #J 对 W1 的偏导，上一个房间的海水*输入 
# delta_B1 = np.sum(delta_Z1, axis=0) / batch_X.shape[0] #J 对 B1 的偏导，上一个房间的海水*1

# 原程序：
# 更新权值（学习率*负梯度）
# W3 = W3 + lr *delta_W3
# W2 = W2 + lr *delta_W2
# W1 = W1 + lr *delta_W1
# 题目一：
# 更新权值(学习率*负梯度) 
W2 = W2 + lr * delta_W2
W1 = W1 + lr * delta_W1

# 改变偏置值
# 原程序：
# b3 = b3 + lr * delta_B3
# b2 = b2 + lr * delta_B2
# b1 = b1 + lr * delta_B1
# 题目一：
b2 = b2 + lr * delta_B2 
b1 = b1 + lr * delta_B1

将本文上面的原代码的第127-133行修改为：

# 原程序这段注释掉
# 输出层输出
# A3 = sigmoid(np.dot(A2,W3) + b3)

# 原程序：
# 计算 loss 值（平方损失函数）
# print('A3:', A3)
# print('epochs:', idx_epoch, 'loss:', np.mean(np.square(T - A3) / 2))
# 保存 loss 值
# loss.append(np.mean(np.square(T - A3) / 2))
# 题目一：
# 计算 loss 值(平方损失函数)
print('A2:', A2)
print('epochs:', idx_epoch, 'loss:', np.mean(np.square(T - A2) / 2))
# 保存 loss 值
loss.append(np.mean(np.square(T - A2) / 2))

将本文上面的原代码的第145-148行修改为：

# 原程序这段注释掉
# 输出层输出
# A3 = sigmoid(np.dot(A2, W3) + b3)

# 原程序：
# print('output:')
# print(A3)
# 题目一：
print('output:') 
print(A2)

最后结果:
A2: [[0.65960453 0.635583 ]]
epochs: 0 loss: 0.06216720544757777
A2: [[0.94857959 0.94838368]]
epochs: 1000 loss: 0.0013270758133718764
A2: [[0.96536305 0.96517664]]
epochs: 2000 loss: 0.000603096268131278
A2: [[0.97240442 0.9722256 ]]
epochs: 3000 loss: 0.0003832333922414345
A2: [[0.97647243 0.97630231]]
epochs: 4000 loss: 0.0002787818153690212
A2: [[0.97919 0.97902823]]
epochs: 5000 loss: 0.000218217846462418
A2: [[0.98116448 0.98101033]]
epochs: 6000 loss: 0.00017884613966145948
A2: [[0.98268007 0.98253276]]
epochs: 7000 loss: 0.00015127107169001484
A2: [[0.98388943 0.98374826]]
epochs: 8000 loss: 0.0001309173245098213
A2: [[0.9848827 0.98474705]]
epochs: 9000 loss: 0.00011529633498690287
output:
[[0.98571613 0.98558545]]

loss与epochs对应图像：

2）如果增加一个样本，李四(0.1,1.0,0)，分别对应李四的学习成绩， 李四的实践成绩，李四被招聘可能性的真值，代码应该如何修改?此时是一个 样本计算一次偏导、更新一次权值，还是两个样本一起计算一次偏导、更新一 次权值?(提示:注意 batch_size 的作用)

将输入数据改为
X = np.array([[1, 0.1], [0.1, 1]])
将标签也叫真值改为
T = np.array([[1], [0]])
此时是一个样本计算一次偏导、更新一次权值，batch_size 将所有样本分组，每组大小为 1，即每次只允许一组样本参与更新权值。

程序结果为：
A3: [[0.5106756] [0.5136808]]
epochs: 0 loss: 0.12582658182316436
A3: [[0.50492621] [0.49714265]]
epochs: 1000 loss: 0.12306221713433124
A3: [[0.55145739] [0.4765768 ]]
epochs: 2000 loss: 0.10707898031720711
A3: [[0.79907552] [0.23582744]]
epochs: 3000 loss: 0.023996307445831908
A3: [[0.89793827] [0.12427739]]
epochs: 4000 loss: 0.006465366449814341
A3: [[0.9279318 ] [0.08906726]]
epochs: 5000 loss: 0.0032817005882779336
A3: [[0.94241068] [0.07179349]]
epochs: 6000 loss: 0.002117708597520987
A3: [[0.95110367] [0.06132146]]
epochs: 7000 loss: 0.00153779320891565
A3: [[0.95698569] [0.05418726]]
epochs: 8000 loss: 0.0011966225420074644
A3: [[0.96127506] [0.04895763]]
epochs: 9000 loss: 0.0009741174976926829
output:
[[0.96456416] [0.04493075]]

loss与epochs对应图像

3）样本为张三[1,0.1,1]、李四[0.1,1,0]、王五[0.1,0.1,0]、赵六[1,1,1]， 请利用 batch_size 实现教材 279 页提到的“批量梯度下降”、“随机梯度下 降”和“小批量梯度下降”，请注意“随机梯度下降”和“小批量梯度下降” 要体现随机性。

批量梯度下降代码修改：
将输入数据改为：

# 输入数据 4 行 2 列
X = np.array([[1, 0.1],
              [0.1, 1], 
              [0.1, 0.1], 
              [1, 1]])

将标签也叫真值改为

T = np.array([[1],
              [0], 
              [0], 
              [1]])

将 batch_size 改为

# 将所有样本分组，每组大小为 
batch_size = 4

程序结果为：
A3: [[0.5109672 ] [0.51398372] [0.50674411] [0.51771357]]
epochs: 0 loss: 0.12409026723021045
A3: [[0.50515753] [0.50492596] [0.49668941] [0.51230716]]
epochs: 1000 loss: 0.12304549696538358
A3: [[0.5110033 ] [0.50485224] [0.49442955] [0.51936102]]
epochs: 2000 loss: 0.1211834951878431
A3: [[0.52255645] [0.50173018] [0.48773956] [0.53274962]]
epochs: 3000 loss: 0.11698729025844672
A3: [[0.55138902] [0.48408108] [0.46626306] [0.56295739]]
epochs: 4000 loss: 0.10549922396433618
A3: [[0.63827074] [0.40389033] [0.39441879] [0.64329999]]
epochs: 5000 loss: 0.07209706608387043
A3: [[0.7809243 ] [0.25394768] [0.26437739] [0.77203507]]
epochs: 6000 loss: 0.029293375123006893
A3: [[0.86235873] [0.1639588 ] [0.1777654 ] [0.85107182]]
epochs: 7000 loss: 0.012450968471902371
A3: [[0.8996153 ] [0.12162389] [0.13406224] [0.88941274]]
epochs: 8000 loss: 0.006883960618183701
A3: [[0.91965358] [0.09845395] [0.10934554] [0.91067088]]
epochs: 9000 loss: 0.004510608328606875
output:
[[0.93206521] [0.08392809] [0.09358011] [0.92406636]]

loss与epochs对应图像：

随机梯度下降代码修改：
在批量梯度下降中的代码的基础上将每次选做去更新权值的 batch_X 做如下修改（本文上面的原代码第116-120行），并在开头加载库部分import random：

for idx_batch in range(max_batch): 
   # 更新权值
   rand = random.randint(0,3) 
   batch_X = X[rand:(rand + 1), :] 
   batch_T = T[rand:(rand + 1), :] 
   update()

程序结果为:
A3: [[0.51680769] [0.51986553] [0.51251153] [0.52365761]]
epochs: 0 loss: 0.12416313957353628
A3: [[0.54803288] [0.54798095] [0.5387816 ] [0.55600262]]
epochs: 1000 loss: 0.12399708611745791
A3: [[0.59231975] [0.58554882] [0.57356581] [0.60178406]]
epochs: 2000 loss: 0.1245780356360811
A3: [[0.57903518] [0.55724209] [0.54192421] [0.5900266 ]]
epochs: 3000 loss: 0.11868627125755232
A3: [[0.56192842] [0.49431689] [0.47585431] [0.57400497]]
epochs: 4000 loss: 0.10552062269916751
A3: [[0.64361782] [0.40891808] [0.39938016] [0.6486386 ]]
epochs: 5000 loss: 0.07214769997593248
A3: [[0.77108709] [0.24540571] [0.25512889] [0.76216996]]
epochs: 6000 loss: 0.029284870849640935
A3: [[0.86170695] [0.16393193] [0.17701343] [0.85079257]]
epochs: 7000 loss: 0.012449406918194055
A3: [[0.90606209] [0.12815832] [0.14068678] [0.89709948]]
epochs: 8000 loss: 0.006953771621462523
A3: [[0.9225112 ] [0.10146093] [0.11233657] [0.91414994]]
epochs: 9000 loss: 0.004536071553560694
output:
[[0.93142185] [0.08358248] [0.09321782] [0.92308014]]

loss与epochs对应图像

小批量梯度下降：
当采用两个样本进行权值更新时代码修改:
在批量梯度下降中的代码的基础上将每次选做去更新权值的 batch_X 做如下修改（本文上面的原代码第116-120行），并在开头加载库部分import random：

for idx_batch in range(max_batch): 
   rand1 = random.randint(0, 3) 
   rand2 = random.randint(0, 3) 
   while rand2 == rand1:
       rand2 = random.randint(0, 3)
   batch_X = np.r_[X[rand1:(rand1 + 1), :],X[rand2:(rand2 + 1), :]] 
   batch_T = np.r_[T[rand1:(rand1 + 1), :],T[rand2:(rand2 + 1), :]] 
   update()

程序运行结果:
A3: [[0.51101251] [0.51402926] [0.50678851] [0.51775982]]
epochs: 0 loss: 0.12409062869766667
A3: [[0.47140124] [0.47119817] [0.46385904] [0.47781223]]
epochs: 1000 loss: 0.12366120504090591
A3: [[0.55390078] [0.54725543] [0.53623975] [0.56266035]]
epochs: 2000 loss: 0.12216400730002658
A3: [[0.51307516] [0.49251482] [0.47914038] [0.52291639]]
epochs: 3000 loss: 0.11710636488246251
A3: [[0.56080513] [0.49377428] [0.47594891] [0.57232262]]
epochs: 4000 loss: 0.10576756028860006
A3: [[0.63997865] [0.40891024] [0.39891656] [0.64535501]]
epochs: 5000 loss: 0.0727163055395233
A3: [[0.78296002] [0.26028359] [0.26922551] [0.77551591]]
epochs: 6000 loss: 0.02971617296197624
A3: [[0.86653149] [0.1697076 ] [0.18372417] [0.855804 ]]
epochs: 7000 loss: 0.012645196439043233
A3: [[0.89842984] [0.12143254] [0.13407257] [0.88772966]]
epochs: 8000 loss: 0.006955305143143153
A3: [[0.92011582] [0.09927472] [0.11062162] [0.91082737]]
epochs: 9000 loss: 0.004553231457453375
output:
[[0.93175521] [0.08399582] [0.09389511] [0.92342789]]

loss与epochs对应图像

小批量梯度下降：
当采用三个样本进行权值更新时代码修改：
在批量梯度下降中的代码的基础上将每次选做去更新权值的 batch_X 做如下修改（本文上面的原代码第116-120行），并在开头加载库部分import random：

for idx_batch in range(max_batch): 
   rand1 = random.randint(0, 3) 
   rand2 = random.randint(0, 3) 
   while rand2 == rand1:
       rand2 = random.randint(0, 3)
   rand3 = random.randint(0, 3)
   while rand3 == rand1 or rand2 == rand3:
       rand3 = random.randint(0, 3)
   batch_X = np.r_[np.r_[X[rand1:(rand1 + 1), :], X[rand2:(rand2 + 1), :]], X[rand3:(rand3+1), :]] 
   batch_T = np.r_[np.r_[T[rand1:(rand1 + 1), :], T[rand2:(rand2 + 1), :]], T[rand3:(rand3+1), :]] 
   update()

程序运行结果:
A3: [[0.5090206 ] [0.51202311] [0.50482209] [0.515732 ]]
epochs: 0 loss: 0.12407365964877877
A3: [[0.51218226] [0.5120278 ] [0.50368338] [0.51943165]]
epochs: 1000 loss: 0.12309768630127152
A3: [[0.52217983] [0.5159698 ] [0.50535549] [0.53067428]]
epochs: 2000 loss: 0.12127346876216516
A3: [[0.51401743] [0.49366755] [0.47998374] [0.52403915]]
epochs: 3000 loss: 0.11710122956111589
A3: [[0.56150737] [0.49478399] [0.47639551] [0.57334834]]
epochs: 4000 loss: 0.1057589128514413
A3: [[0.62082634] [0.39082067] [0.38145679] [0.6260715 ]]
epochs: 5000 loss: 0.07273065833654883
A3: [[0.78283596] [0.25844977] [0.26838593] [0.77448454]]
epochs: 6000 loss: 0.029605592029020987
A3: [[0.86168136] [0.1644539 ] [0.17814641] [0.8504383 ]]
epochs: 7000 loss: 0.01253524732284944
A3: [[0.90040608] [0.1228263 ] [0.13532646] [0.89039469]]
epochs: 8000 loss: 0.006916478154456151
A3: [[0.91903288] [0.09822367] [0.10901387] [0.91002251]]
epochs: 9000 loss: 0.004522942113958385
output:
[[0.93235515] [0.08450808] [0.0940331 ] [0.92459731]]

loss与epochs对应图像：

4）【选做】本例中输入向量、真值都是行向量，请将它们修改为列向量， 如 X = np.array([[1,0.1]])改为 X = np.array([[1],[0.1]])，请合理修改其 它部分以使程序得到与行向量时相同的结果。(不允许直接使用 X 的转置进行 全局替换)

修改后的代码采用批量梯度下降，修改的大致思路是：
将 $\mathbf{W}$ 与 $\mathbf{b}$ 进行转置， 再将 $\mathbf{Z}$ 的计算和 $\mathbf{A}$ 的计算由 $\mathbf{A}\ast \mathbf{W}$ 变为 $\mathbf{W}\ast \mathbf{A}$ ， $\mathbf{delt}{\mathbf{a}}_{\mathbf{W}}$ 的计算由 $\mathbf{A}\ast \mathbf{Z}$ 变为 $\mathbf{Z}\ast \mathbf{A}$ ，$\mathbf{delt}{\mathbf{a}}_{\mathbf{B}}$ 的计算由 $\mathbf{delt}{\mathbf{a}}_{\mathbf{Z}}$ 按列求和变为按行求和，由于$\mathbf{delt}{\mathbf{a}}_{\mathbf{B}}$ 经过 np.sum 计算后， 其被压缩为一维的行向量，所以要对 $\mathbf{delt}{\mathbf{a}}_{\mathbf{B}}$ 进行 reshape，使其成为二维列向量才可以进行偏置的更新计算，$\mathbf{delt}{\mathbf{a}}_{\mathbf{A}}$ 的计算由 $\mathbf{Z}\ast \mathbf{W}$ 变为 $\mathbf{W}\ast \mathbf{Z}$ 。
修改部分代码如下：
将本文上面的原代码的第4-37行修改为：

# 输入数据 2 行 4 列
X = np.array([[1, 0.1, 0.1, 1],
             [0.1, 1, 0.1, 1]]) 
# 标签，也叫真值，1 行 4 列
T = np.array([[1, 0, 0, 1]])

# 输入层到隐藏层的权值初始化，2 行 2 列，同一列是从同一个节点发出的权值 
W1 = np.array([[0.8, 0.2],
              [0.2, 0.8]])
# 隐藏层到输出层的权值初始化，2 行 2 列
W2 = np.array([[0.5,0.5], 
              [0.0,1.0]])
# 隐藏层 2 到输出层的权值初始化，1 行 2 列 
W3 = np.array([[0.5, 0.5]])

# 隐藏层 1 的 2 个神经元偏置 
b1 = np.array([[-1],
              [0.3]])       
# 输出层的 2 个神经元偏置
b2 = np.array([[0.1], 
              [-0.1]])
# 输出层的 1 个神经元偏置 
b3 = np.array([[-0.6]])

将本文上面的原代码的第45行修改为：

# 将所有样本分组，每组大小为
batch_size = 4

将本文上面的原代码的第59-69行修改为：

# 隐藏层 1 输出
Z1 = np.dot(W1,batch_X) + b1 
A1 = sigmoid(Z1)

# 隐藏层 2 输出
Z2 = (np.dot(W2, A1) + b2) 
A2 = sigmoid(Z2)

# 输出层输出 
Z3=(np.dot(W3, A2) + b3) 
A3 = sigmoid(Z3)

将本文上面的原代码的第75-96行修改为：

# 利用输出层的误差，求出偏导(即隐藏层 2 到输出层的权值改变)
# 由于一次计算了多个样本，所以需要求平均
delta_W3 = delta_Z3.dot(A2.T) / batch_X.shape[1] #J 对 W3 的偏导，上一个房间的海水*A2
delta_B3 = np.sum(delta_Z3, axis=1) / batch_X.shape[1] #J 对 B3 的偏导，上一个房间的海水*1

# 求隐藏层 2 的误差
delta_A2 = W3.T.dot(delta_Z3) #J 对 A2 的偏导，上一个房间的海水*W3
delta_Z2 = delta_A2 * dsigmoid(A2) #J 对 Z2 的偏导，上一个房间的海水*A2*(1-A2)

# 利用隐藏层 2 的误差，求出偏导(即隐藏层 1 到隐藏层 2 的权值改变)
# 由于一次计算了多个样本，所以需要求平均
delta_W2 = delta_Z2.dot(A1.T) / batch_X.shape[1] #J 对 W2 的偏导，上一个房间的海水*A1
delta_B2 = np.sum(delta_Z2, axis=1) / batch_X.shape[1] #J 对 B2 的偏导，上一个房间的海水*1

# 求隐藏层 1 的误差
delta_A1 = W2.T.dot(delta_Z2) #J 对 A1 的偏导，上一个房间的海水*W2
delta_Z1 = delta_A1 * dsigmoid(A1) #J 对 Z1 的偏导，上一个房间的海水*A1*(1-A1)

# 利用隐藏层 1 的误差，求出偏导(即输入层到隐藏层 1 的权值改变)
# 由于一次计算了多个样本，所以需要求平均
delta_W1 = delta_Z1.dot(batch_X.T) / batch_X.shape[1] #J 对 W1 的偏导，上一个房间的海水*输入 
delta_B1 = np.sum(delta_Z1, axis=1) / batch_X.shape[1] #J 对 B1 的偏导，上一个房间的海水*1

将本文上面的原代码的第103-106行修改为：

# 改变偏置值
n3 = delta_B3.shape[0]
delta_b3 = delta_B3.reshape(n3,1) 
b3 = b3 + lr * delta_b3
n2 = delta_B2.shape[0]
delta_b2 = delta_B2.reshape(n2,1) 
b2 = b2 + lr * delta_b2
n1 = delta_B1.shape[0]
delta_b1 = delta_B1.reshape(n1,1) 
b1 = b1 + lr * delta_b1

将本文上面的原代码的第112行修改为：

max_batch = X.shape[1] // batch_size

将本文上面的原代码的第117-119行修改为：

# 更新权值
batch_X = X[:, idx_batch*batch_size:(idx_batch+1)*batch_size] 
batch_T = T[:, idx_batch*batch_size:(idx_batch+1)*batch_size]

将本文上面的原代码的第123-128行修改为：

# 隐藏层 1 输出
A1 = sigmoid(np.dot(W1, X) + b1)

# 隐藏层 2 输出
A2 = sigmoid(np.dot(W2, A1) + b2)

# 输出层输出
A3 = sigmoid(np.dot(W3, A2) + b3)

修改后程序结果:
A3: [[0.5109672 0.51398372 0.50674411 0.51771357]]
epochs: 0 loss: 0.12409026723021045
A3: [[0.50515753 0.50492596 0.49668941 0.51230716]]
epochs: 1000 loss: 0.12304549696538358
A3: [[0.5110033 0.50485224 0.49442955 0.51936102]]
epochs: 2000 loss: 0.12118349518784312
A3: [[0.52255645 0.50173018 0.48773956 0.53274962]]
epochs: 3000 loss: 0.11698729025844672
A3: [[0.55138902 0.48408108 0.46626306 0.56295739]]
epochs: 4000 loss: 0.10549922396433616
A3: [[0.63827074 0.40389033 0.39441879 0.64329999]]
epochs: 5000 loss: 0.07209706608387037
A3: [[0.7809243 0.25394768 0.26437739 0.77203507]]
epochs: 6000 loss: 0.029293375123006875
A3: [[0.86235873 0.1639588 0.1777654 0.85107182]]
epochs: 7000 loss: 0.012450968471902364
A3: [[0.8996153 0.12162389 0.13406224 0.88941274]]
epochs: 8000 loss: 0.006883960618183695
A3: [[0.91965358 0.09845395 0.10934554 0.91067088]]
epochs: 9000 loss: 0.004510608328606874
output:
[[0.93206521 0.08392809 0.09358011 0.92406636]]

loss与epochs对应图像：

其结果与输入和输出均为行向量时的批量梯度下降结果一致。

实验结果与分析

1)、2)、3)、4)这几个小题的实验中，在迭代次数达到 10000 次时，都达到了相对可观的效果。
在 2)小题中，样本增加了一个也使梯度下降的速度变小了。
最初的代码跑出来的结果：
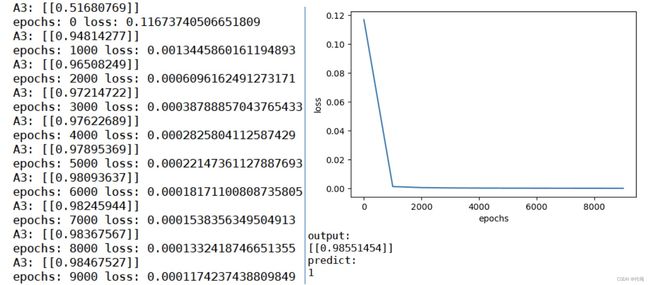可以明显的看出来一个样本时梯度下降的速度要快于两个样本时。
在第 3)小题中，因为样本数较小，所以梯度下降的速度很难看出明显差别。 但是在理论上，梯度下降的速度：随机梯度下降 >小批量梯度下降>批量梯度下 降。因为随机梯度下降只用一个样本迭代，故训练速度极快，但是迭代方向变化很大，准确度较低。而批量梯度下降因为训练的样本量很大，所以训练速度会很慢，但是准确度较高。小批量梯度下降结合了上述两种方式的优缺点。
在第 4)小题中，不管是将样本按行输入还是按列输入，最后的结果和梯度下降的速度都一样。但是代码中的一些参数和公式要配合修改。

实验小结

这个实验有难度的也就第4)小题，想清楚矩阵的变换后问题也就迎刃而解了，另外要清楚求偏导用python怎么写。