【数据结构】链式二叉树的基本操作：定义、遍历访问、创建、输出、总结点数、叶子结点数、深度、镜像

前言

理论基础知识看这里【数据结构】树的基础知识：树和二叉树的逻辑结构与性质-CSDN博客https://blog.csdn.net/2301_76172693/article/details/133954565?spm=1001.2014.3001.5501二叉树的存储表示有顺序和链式两种。顺序存储通过数组实现，常用于存储完全二叉树，因为可以通过存储顺序比较直观看出结点在完全树中的位置。并且，完全二叉树在操作过程中，大小和形态不发生剧烈变化。编号(下标)从0开始，编号顺序为层序遍历。在本节中，进行的工作是将二叉树这一非线性的结构以一定的顺序(前序，中序，后序，或者直接是顺序表)排成线性结构。

#define MAX 100
typedef char DataType;
typedef struct{
  char BiTree[MAX]；//存储数组,MAX为最多结点个数
  int n;//当前结点个数
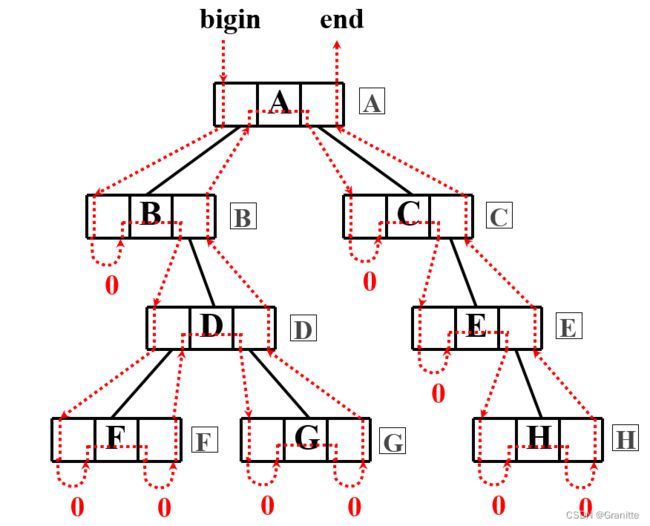
}BiTree；

 一般二叉树做不到结点编号的连续，用顺序存储会浪费空间。故常用链式存储。链式存储有多种形式，本文采用孩子结点表示的二叉链表。

基本操作

定义结构

tyoedef char DataType;
typedef struct BiTNode{
  DataType data;//数据域
  BiTNode *lchild,*rchild;//左右孩子指针域
}BiTNode,*BiTree;

遍历访问

本文涉及的二叉树的操作都与遍历密切相关。下面介绍三种遍历二叉树的顺序。掌握这三种顺序的基本代码，并能熟练写出已知二叉树的遍历结果。本部分代码中的访问函数和printf在实际应用中换成对应的操作函数即可。T可为引用型参数。

对于递归，如果你不清楚它的具体执行过程，不要纠结。递归的精髓在于整体的逻辑正确和递归出口的确定。如果对递归过于模糊，可先了解阶乘、等差数列、斐波那契数列、汉诺塔等经典递归问题。

前序遍历(先序遍历)

前序遍历的过程:

1. 访问根结点
2. 前序遍历左子树
3. 前序遍历右子树

void PerOrder(BiTree T)
{
 if(T!=NULL)//递归出口:发现某子树的根结点为空//递归出口
 {
  printf("%c\n",T->data);//访问根结点
  PerOrder(T->lchild);//调用函数，前序遍历左子树
  PerOrder(T->rchild);//调用函数，前序遍历右子树
 }
}

 第一个被访问的一定是二叉树的根，若根的左子树非空，则在根后紧随的一定是左子树的左孩子；若左子女为空，则紧随其后的是其右子女。遍历访问实际上是一个递归过程。例如，在访问完B时，先探寻其lchild，发现是空指针，于是返回到B,再探寻其rchild,发现指向D,于是访问B。

中序遍历

中序遍历的过程:

1. 中序遍历左子树
2. 访问根结点
3. 中序遍历右子树

void InOrder(BiTree T)
{
 if(T!=NULL)//递归出口:发现某子树的根结点为空
 {
  InOrder(T->lchild);//调用函数，中序访问左子树
  printf("%c\n",T->data);//访问根结点
  InOrder(T->rchild);//调用函数，中序访问右子树
 }
}

后序遍历

后序遍历的过程:

1. 前序遍历左子树
2. 前序遍历右子树
3. 访问根结点

void BeOrder(BiTree T)
{
 if(T!=NULL)//递归出口:发现某子树的根结点为空
 {
  BeOrder(T->lchild);//调用函数，后序遍历左子树
  BeOrder(T->rchild);//调用函数，后序遍历右子树
  printf("%c",T->data);//访问根结点
 }
}

练习

可通过这几道题检测学习成果：

1.设有如图所示的二叉树。

① 分别用顺序存储方法和链接存储方法画出该二叉树的存储结构。

② 写出该二叉树的先序、中序、后序遍历序列。

2.已知一棵二叉树的先序遍历序列和中序遍历序列分别为ABDGHCEFI和GDHBAECIF，请画出这棵二叉树，然后给出该树的后序遍历序列。

3. 设一棵二叉树的中序遍历序列和后序遍历序列分别为BDCEAFHG和DECBHGFA ，请画出这棵二叉树，然后给出该树的先序序列。

前序遍历创建

实质是创建一个二叉链表。需要让程序知道哪个是空结点，哪个不是。一般输入“*”或“#”表示空结点。

void Creatree(BiTree &T)
{
 char ch;
 scanf("%c",&ch);
 if(ch=='*') T=NULL;
  T->data=NULL;
  return;
 }
 else
 {
  T=(BiTNode*)malloc//别忘了分配空间！！！！！！
  T->data=ch;
  Creatree(T->lchild);
  Creatree(T->rchjild);
 }
}

前序遍历输出 

这是一个和遍历模板很像的实例

void Printree(BiTree T)
{
 if(T!=NULL)
 {
  printf("%c",T->data);
  Printree(T->lchild);
  Printree(T->rchild);   
 }
}

统计结点个数

void CountTree(BiTree T,int &m)//在函数外，m初始值为0
{
 if(T==NULL) return;//递归出口
 else
 {
  m++;
  CountTree(T->lchild,m);
  CountTree(T->rchild,m);
}
}

统计叶子结点个数

void Countleaf(BiTree T,int &n)
{
 if(T==NULL) return;
 else
 {
  if(T->lchild==NULL&&T->rchild==NULL)  n++;
  Countleaf(T->lchild，n);
  Countleaf(T->rchild，n);
 }
}

后序遍历计算树的深度   

分别计算左、右子树的深度，取大者+1为树的深度。

int TreeDepth(BiTree T)
{//分别求左右子树的深度，取大者加一为树的深度。
    int p, q; p = 0; q = 0;
    if (T == NULL) return 0;
    else
    {
        p = TreeDepth(T->lchild);
        q= TreeDepth(T->rchild);
        if (p > q)
            return p + 1;//加的一是根节点
        else return q+ 1;
    }
}

求镜像二叉树

void MirrorTree(BiTree &T)
{
    if (T == NULL||(T->lchild==NULL&&T->rchild==NULL)) return;
    else
    {
        //交换根节点左右子树
        BiTree t = T->lchild;//交换代码和两个数交换值的原理相同
        T->lchild = T->rchild;
         T->rchild = t;
        //递归交换左子树
        if (T->lchild)
            MirrorTree(T->lchild);
        //递归交换右子树
        if (T->rchild)
            MirrorTree(T->rchild);
    }
}

上机实现

题干重述

建立如图所示的二叉树并进行下列操作：

1. 定义二叉树的结点结构
2. 实现先序序列构造二叉树的算法
3. 实现先序遍历这棵二叉树，输出每个结点的值的算法
4. 利用先序遍历，统计叶子结点的个数
5. 利用后序遍历，求二叉树的深度
6. 求镜像二叉树(交换所有结点的左右子树)

完整代码

部分细节与vs编译器自身有关。

#include 
#include 
typedef struct BiTNode {//定义二叉树节点结构
	char data;
	struct BiTNode *lchild, *rchild;
}BiTreeNode,*BiTree;
void CreateBiTree(BiTree &T) {//先序遍历构造二叉树
    char ch;
    scanf_s("%c", &ch);
    if (ch == '*') T = NULL; //递归出口
    else {
        T = (BiTNode*)malloc(sizeof(BiTNode));
        T->data = ch;              // 生成根结点
        CreateBiTree(T->lchild);   // 构造左子树
        CreateBiTree(T->rchild);   // 构造右子树
    }
}
void PrintTree(BiTree T)//先序遍历输出二叉树
{
    if (T==NULL) return;
    else
    {
        printf("%c\n",T->data);
        PrintTree(T->lchild);
        PrintTree(T->rchild);
    }
}
void CountTree(BiTree T, int& i)//统计结点个数
{
    if (T == NULL) return;
    else
    {
        i++;
        CountTree(T->lchild, i);
        CountTree(T->rchild, i);
    }
}
void CountLeaf(BiTree T, int& j)//统计叶子结点个数
{
    if (T == NULL) return;
    else
    {
        if (T->lchild == NULL && T->rchild == NULL)
            j++;
        CountLeaf(T->lchild, j);
        CountLeaf(T->rchild, j);
    }
}
int TreeDepth(BiTree T)//后序遍历求深度
{
    int p, q; p = 0; q = 0;
    if (T == NULL) return 0;
    else
    {
        p = TreeDepth(T->lchild);
        q= TreeDepth(T->rchild);
        if (p > q)
            return p + 1;//加的一是根节点
        else return q+ 1;
    }
}
void MirrorTree(BiTree &T)//求镜像二叉树
{
    if (T == NULL||(T->lchild==NULL&&T->rchild==NULL)) return;
    else
    {
        //交换根节点左右子树
        BiTree t = T->lchild;
        T->lchild = T->rchild;
         T->rchild = t;
        //递归交换左子树
        if (T->lchild)
            MirrorTree(T->lchild);
        //递归交换右子树
        if (T->rchild)
            MirrorTree(T->rchild);
    }
}
int main(void)
{
    BiTree T;
    printf("先序输出构造二叉树，输入*表示空\n");
    CreateBiTree(T);
    printf("先序遍历输出二叉树\n");
    PrintTree(T);
    int i=0,j=0;
    CountLeaf(T,i);
    CountTree(T,j);
    printf("该树有%d个叶子结点，共有%d个结点\n", i, j);
    int m=TreeDepth(T);
    printf("树的深度为%d", m);
    MirrorTree(T);
    printf("先序输出镜像二叉树\n");
    PrintTree(T);
    return 0;
}

运行结果