单调栈经典问题整理
下一个更大的问题
1、下一个更大元素 I
class Solution:
def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
m, stack = defaultdict(lambda: -1), deque()
for num in nums2:
while stack and stack[-1] < num:
cur = stack.pop()
m[cur] = num
stack.append(num)
res = []
for num in nums1:
res.append(m[num])
return res 2、下一个更大元素 II
class Solution:
def nextGreaterElements(self, nums: List[int]) -> List[int]:
nums2 = nums * 2
m, stack = defaultdict(lambda: -1), deque()
for i, num in enumerate(nums2):
while stack and nums2[stack[-1]] < num:
cur = stack.pop()
m[cur] = num
stack.append(i)
res = []
for i,num in enumerate(nums):
res.append(m[i])
return res3、下一个更大元素 IV
class Solution:
def secondGreaterElement(self, nums: List[int]) -> List[int]:
res, first, second = [-1] * len(nums), [], deque()
for i, x in enumerate(nums):
temp = deque()
while second and nums[second[-1]] < x:
res[second.pop()] = x
while first and nums[first[-1]] < x:
temp.append(first.pop())
while temp:
second.append(temp.pop())
first.append(i)
return res4、每日温度
class Solution:
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
res, stack = [0] * len(temperatures), deque()
temperatures = [0] + temperatures
for i, t in enumerate(temperatures):
while stack and temperatures[stack[-1]] < t:
cur = stack.pop()
if cur > 0:
res[cur - 1] = i - cur
stack.append(i)
return res单调栈与二叉树
1、验证前序遍历的二叉搜索树
class Solution:
def verifyPreorder(self, preorder: List[int]) -> bool:
minl, st = 0, deque()
for num in preorder:
if num < minl: return False
while st and num > st[-1]:
minl = st[-1]
st.pop()
st.append(num)
return True2、前序遍历构造二叉搜索树
class Solution:
def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:
st, res = deque(), None
for val in preorder:
cur = None
while st and val > st[-1].val:
cur = st.pop()
if cur:
cur.right = TreeNode(val)
st.append(cur.right)
else:
nd = TreeNode(val)
if st: st[-1].left = nd
else: res = nd
st.append(nd)
return res3、叶值的最小代价生成树
class Solution:
def mctFromLeafValues(self, arr: List[int]) -> int:
stack = []
mct = 0
for num in arr:
while stack and num > stack[-1]:
min_1 = stack.pop()
if stack:
min_2 = min(stack[-1],num)
else:
min_2 = num
mct = mct + min_1 * min_2
stack.append(num)
while len(stack) > 1:
mct = mct + stack.pop() * stack[-1]
return mct; 4、给定二叉搜索树的插入顺序求深度
class Solution:
def maxDepthBST(self, order: List[int]) -> int:
n = len(order)
father, occur, stack = [0] * (n + 1), [0] * (n + 1), []
for i, x in enumerate(order, 1): occur[x] = i
for x, i in enumerate(occur):
while stack and occur[stack[-1]] > i:
if occur[father[stack[-1]]] < i:
father[stack[-1]] = x
stack.pop()
if stack:
father[x] = stack[-1]
stack.append(x)
for x in order:
father[x] = 1 + father[father[x]]
return max(father)图形单调栈
1、接雨水
class Solution:
def trap(self, heights: List[int]) -> int:
stack, res = [], 0
for i in range(len(heights)):
while stack and heights[stack[-1]] < heights[i]:
cur = stack.pop()
if not stack: break
res += (min(heights[stack[-1]], heights[i]) - heights[cur]) * (i - stack[-1] - 1)
stack.append(i)
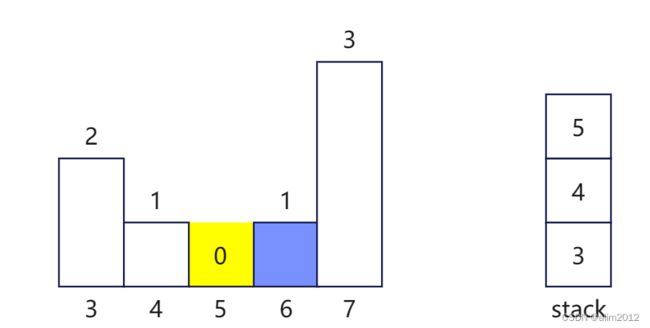
return res2、柱状图中最大的矩形
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
stack, heights = [], [0] + heights + [0]
res = 0
for i in range(len(heights)):
while stack and heights[stack[-1]] > heights[i]:
cur = stack.pop()
res = max(res, (i - stack[-1] - 1)* heights[cur])
stack.append(i)
return res3、统计全 1 子矩形
class Solution:
def numSubmat(self, mat: List[List[int]]) -> int:
m, n = len(mat), len(mat[0])
row = [[0] * n for _ in range(m)]
for i in range(m):
for j in range(n):
if j == 0:
row[i][j] = mat[i][j]
else:
row[i][j] = 0 if mat[i][j] == 0 else row[i][j - 1] + 1
ans = 0
for j in range(n):
Q = list()
total = 0
for i in range(m):
length = 1
while Q and Q[-1][0] > row[i][j]:
# 弹出的时候要减去多于的答案
total -= Q[-1][1] * (Q[-1][0] - row[i][j])
length += Q[-1][1]
Q.pop()
total += row[i][j]
ans += total
Q.append((row[i][j], length))
return ans单调栈与数组
1、去除重复字母
class Solution:
def removeDuplicateLetters(self, s: str) -> str:
n, stack = len(s), []
for i in range(n):
if s[i] in stack:
continue
else:
while stack and stack[-1] > s[i] and stack[-1] in s[i+1:]:
stack.pop()
stack.append(s[i])
return "".join(stack)2、132 模式
class Solution:
def find132pattern(self, nums: List[int]) -> bool:
s = deque([])
k = -float('inf')
for n in reversed(nums):
if n < k: return True
while s and n > s[-1]:
k = max(k, s.pop())
s.append(n)
return False3、最多能完成排序的块
class Solution:
def maxChunksToSorted(self, arr: List[int]) -> int:
#[1,2,0,3] #[2,0,1]
n = len(arr)
nums = arr
stack=[]
for i in range(n):
m = nums[i]
while stack and stack[-1] > nums[i]:
m=max(stack[-1],m)
stack.pop(-1)
stack.append(m)
return len(stack)4、股票价格跨度
class StockSpanner:
def __init__(self):
self.st = deque()
def next(self, price: int) -> int:
w = 0
while self.st and self.st[-1][0] <= price:
w += self.st.pop()[1]
self.st.append((price, w + 1))
return w + 1 5、子数组的最小值之和
class Solution:
def sumSubarrayMins(self, arr: List[int]) -> int:
A.append(-inf)
stack, res=[-1], 0
for i in range(len(A)):
while A[i] < A[stack[-1]]:
idx = stack.pop()
res += A[idx] * (i - idx) * (idx - stack[-1])
stack.append(i)
return res % (10**9 + 7)子数组范围和与上面的题类似,只需要再构建单调递减栈求出最大值的和即可
6、最大宽度坡
class Solution:
def maxWidthRamp(self, nums: List[int]) -> int:
st, maxl = deque(), 0
for i, num in enumerate(nums):
if not st or num < nums[st[-1]]:
st.append(i)
n = len(nums)
for i in reversed(range(n)):
while st and nums[st[-1]] <= nums[i]:
maxl = max(maxl, i - st.pop())
return maxl7、使数组按非递减顺序排列
class Solution:
def totalSteps(self, nums: List[int]) -> int:
ans, st = 0, []
for num in nums:
max_t = 0
while st and st[-1][0] <= num:
max_t = max(max_t, st.pop()[1])
if st: max_t += 1
ans = max(ans, max_t)
st.append((num, max_t))
return ans8、单调栈 + 前缀和 -- 巫师的总力量和
class Solution:
def totalStrength(self, strength: List[int]) -> int:
n = len(strength)
# left[i] 为左侧严格小于 strength[i] 的最近元素位置(不存在时为 -1)
# right[i] 为右侧小于等于 strength[i] 的最近元素位置(不存在时为 n)
left, right, st = [-1] * n, [n] * n, []
for i, v in enumerate(strength):
while st and strength[st[-1]] >= v: right[st.pop()] = i
if st: left[i] = st[-1]
st.append(i)
ss = list(accumulate(accumulate(strength, initial=0), initial=0)) # 前缀和的前缀和
ans = 0
for i, v in enumerate(strength):
l, r = left[i] + 1, right[i] - 1 # [l, r] 左闭右闭
tot = (i - l + 1) * (ss[r + 2] - ss[i + 1]) - (r - i + 1) * (ss[i + 1] - ss[l])
ans += v * tot # 累加贡献
return ans % (10 ** 9 + 7)9、所有子数组最小值中的最大值
思路主要是求最小值的区间和更新最小值两步
一、
1.1 以当前值为最小值,求出能覆盖的最远区间,依次求出左边界和右边界
1.2 相同区间长度的值可能有多个,按题目意思求最大值
二、第一步中可能会存在某个区间长度的值没有求到的情况,有遗漏;
遗漏的时候说明该值和后面较长的区间值相同
由于区间较短的值必定大于等于区间较长的值,因此逆序遍历更新下结果数组
class Solution:
def findMaximums(self, nums: List[int]) -> List[int]:
nums = [0] + nums + [0]
ans = [0] * (len(nums) - 2)
dic = collections.defaultdict(int)
stack = []
for i in range(len(nums)):
while stack and nums[stack[-1]] > nums[i]:
index = stack.pop()
dic[i - stack[-1] - 1]=max(dic[i - stack[-1] - 1], nums[index])
stack.append(i)
for k in dic:
ans[k - 1] = dic[k]
for i in range(len(ans) - 1, 0, -1):
ans[i - 1] = max(ans[i-1],ans[i])
return ans10、找出最具竞争力的子序列 -- 条件单调栈
1、弹出栈时考虑剩余元素个数和栈元素个数是否至少有k个
2、压入栈时考虑栈元素不超过k
class Solution:
def mostCompetitive(self, nums: List[int], k: int) -> List[int]:
st = deque()
for i, n in enumerate(nums):
while st and len(nums) - i + len(st) > k and n < st[-1]:
st.pop()
if len(st) < k: st.append(n)
return list(st)11、 队列中可以看到的人数 -- 逆序单调栈
class Solution:
def canSeePersonsCount(self, heights: List[int]) -> List[int]:
n = len(heights)
res = [0] * n
st = deque([heights[n - 1]])
for j in range(n - 2,-1,-1):
v = heights[j]
while st and v > st[-1]:
res[j] += 1
st.pop()
if st: res[j] += 1
st.append(v)
return res单调队列
1、带限制的子序列和
class Solution:
def constrainedSubsetSum(self, nums: List[int], k: int) -> int:
n = len(nums)
q = deque([(nums[0], 0)])
res, maxl = nums[0], nums[0]
for i in range(1, n):
while i - q[0][1] > k:
q.popleft()
res = max(0, q[0][0]) + nums[i]
maxl = max(maxl, res)
while q and res >= q[-1][0]:
q.pop()
q.append((res, i))
return maxl2、 跳跃游戏 VI
class Solution:
def maxResult(self, nums: List[int], k: int) -> int:
n = len(nums)
q = deque([(nums[0], 0)])
res = nums[0]
for i in range(1, n):
while i - q[0][1] > k:
q.popleft()
res = q[0][0] + nums[i]
while q and res >= q[-1][0]:
q.pop()
q.append((res, i))
return res参考资料:
单调栈 + 前缀和的前缀和(Python/Java/C++/Go)
单调栈求区间
42. 接雨水 - 接雨水 - 力扣(LeetCode)