机器学习——特征降维

【说明】文章内容来自《机器学习——基于sklearn》，用于学习记录。若有争议联系删除。

1、简介

        特征降维是指减少特征个数，最终结果就是特征和特征之间不相关。

        由于特征矩阵过大，会导致计算量大、训练时间长,因此降低特征矩阵维度必不可少，特征降维是通过选取有代表性的特征，减少特征个数，得到一组不相关主变量的过程。具有如下作用:

1. 降低时间的复杂度和空间复杂度，
2. 使得较简单的模型具有更强的鲁棒性，
3. 便于实现数据的可视化。

        特征降维具有线性判别分析(Linear Discriminant Analysis, LDA)和主成分分析(Principal Component Analysis, PCA)等方法。LDA 和PCA有很多相似之处，其本质是将原始的样本映射到维度更低的样本空间中。但是PCA 和 LDA的映射目标不一样，具体如下：

1. LDA是为了让映射后的样本有最好的分类性能,而PCA是为了让映射后的样本具有最大的发散性。
2. LDA是有监督的降维方法,而PCA是无监督的降维方法。
3. LDA最多降到类别减1的维数,而PCA没有这个限制。
4. LDA除了可以用于降维,还可以用于分类。

2、线性判别分析

 2.1 线性判别分析简介

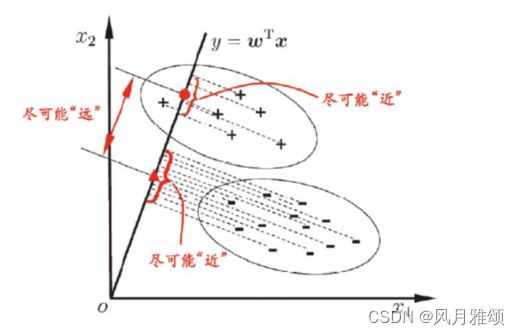
        线性判别分析是一种经典的降维方法。现假设有红、蓝两色的二维数据，投影到一维,要求同色数据的投影点尽可能接近，不同色数据的投影点尽可能远，使得红色数据中心和蓝色数据中心的距离尽可能大。
        线性判别分析就是寻找这样的一条线:,使得投影后类内方差最小，类间方差最大。

2.2 线性判别示例

        Sklearn 提供discriminant_analysis.LinearDiscriminantAnalysis用于线性判别分析，具体语法如下所示：

 LinearDiscriminantAnalysis (n_components=n)

【参数说明】n_components=n等号右侧的n代表减少的维数。

示例：

import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

iris = datasets.load_iris()
x = iris.data
y = iris.target
target_names = iris.target_names
lda = LinearDiscriminantAnalysis(n_components = 2)
#fit(x,y)传两个参数的是有监督学习的算法，两个参数分别对应这特征和目标值
x_r2 = lda.fit(x,y).transform(x)
plt.figure()
for c,i,target_name in zip('rgb', [0,1,2], target_names):
    plt.scatter(x_r2[y == i, 0], x_r2[y ==i, 1], c=c, label = target_name)
plt.legend()
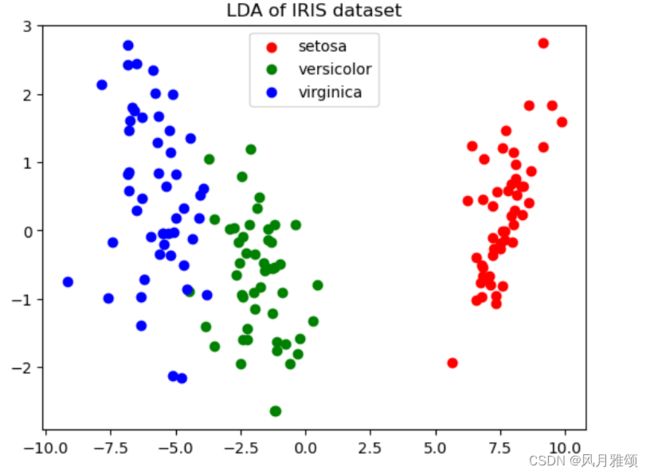
plt.title('LDA of IRIS dataset')
plt.show()

【运行结果】

3、主成分分析

3.1 简介

        在多变量的问题中，变量之间往往存在信息重叠，通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。PCA将重复的变量或关系紧密的变量删去。 PCA算法的主要优点如下所示：

1. 仅仅需要以方差衡量信息量，不受数据集以外的因素影响。
2. 各主成分之间正交，可消除原始数据成分间的相互影响的因素。
3. 计算方法简单，主要运算是特征值分解，易于实现。

主要缺点：

1. 主成分各个特征维度的含义具有一定的模糊性。
2. 非主成分也可能含有样本差异的重要信息。

3.2 PCA函数

        Sklearn 提供decomposition.PCA用于主成分分析，具体语法如下所示：

PCA(n_components=n)

【参数说明】n_components取值有小数和整数，小数时，表示保留百分比；整数，表示保留特征数。

示例：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_blobs
#make_blods:多类单标签数据集，为每个类分配一个或多个正态分布的点集
#x为样本特征，y为样本簇类别。共1000个样本，没个样本3个特征，共4个簇
x,y = make_blobs(n_samples = 10000, n_features = 3, 
                 centers = [[3,3,3],[0,0,0],[1,1,1],[2,2,2]], cluster_std = [0.2, 0.1, 0.2, 0.2],
                random_state = 9)

fig = plt.figure()
ax = Axes3D(fig, rect = [0,0,1,1], elev = 30, azim = 20)
plt.scatter(x[:, 0], x[:, 1], x[:, 2],marker = 'o')

【运行结果】

 scale = np.sqrt(self._sizes) * dpi / 72.0 * self._factor

from sklearn.decomposition import PCA
pca = PCA(n_components = 3)#降维后需要的维度
pca.fit(x)
print(pca.explained_variance_ratio_)#方差比例
print(pca.explained_variance_)

【运行结果】

【分析】

投影后3个维度的方差分别为98.3%，0.85%，0.83%，第一个特征占了绝大多数。

采用主成分分析进行降维。

（1）n_components取整数

from sklearn.decomposition import PCA
pca = PCA(n_components = 2)#降维后需要的维度
pca.fit(x)
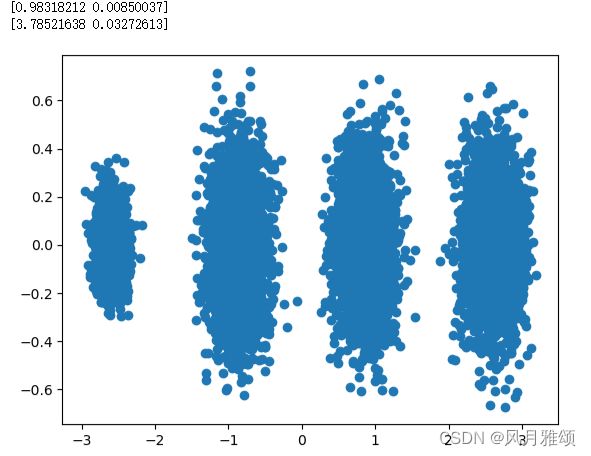
print(pca.explained_variance_ratio_)#方差比例
print(pca.explained_variance_)
x_new = pca.transform(x)
plt.scatter(x_new[:,0],x_new[:,1],marker = 'o')
plt.show()

【运行结果】

（2）n_components取小数

pca = PCA(n_components = 0.95)#降维后需要的维度
pca.fit(x)
print(pca.explained_variance_ratio_)#方差比例
print(pca.explained_variance_)
print(pca.n_components_)

【运行结果】

【结果分析】

        只有第一个投影特征被保留。这是由于第一个主成分占投影特征的方差比例高达98.3%，只选择这个特征维度便可满足95%的阈值要求。