蓝桥杯python基础练习

1、龟兔赛跑预测

话说这个世界上有各种各样的兔子和乌龟，但是研究发现，所有的兔子和乌龟都有一个共同的特点——喜欢赛跑。于是世界上各个角落都不断在发生着乌龟和兔子的比赛，小华对此很感兴趣，于是决定研究不同兔子和乌龟的赛跑。他发现，兔子虽然跑比乌龟快，但它们有众所周知的毛病——骄傲且懒惰，于是在与乌龟的比赛中，一旦任一秒结束后兔子发现自己领先t米或以上，它们就会停下来休息s秒。对于不同的兔子，t，s的数值是不同的，但是所有的乌龟却是一致——它们不到终点决不停止。
　　然而有些比赛相当漫长，全程观看会耗费大量时间，而小华发现只要在每场比赛开始后记录下兔子和乌龟的数据——兔子的速度v1（表示每秒兔子能跑v1米），乌龟的速度v2，以及兔子对应的t，s值，以及赛道的长度l——就能预测出比赛的结果。请你写一个程序，对于输入的一场比赛的数据v1，v2，t，s，l，预测该场比赛的结果。
输入格式
　　输入只有一行，包含用空格隔开的五个正整数v1，v2，t，s，l，其中(v1,v2<=100;t<=300;s<=10;l<=10000且为v1,v2的公倍数)
输出格式
输出包含两行，第一行输出比赛结果——一个大写字母“T”或“R”或“D”，分别表示乌龟获胜，兔子获胜，或者两者同时到达终点。
　　第二行输出一个正整数，表示获胜者（或者双方同时）到达终点所耗费的时间（秒数）。

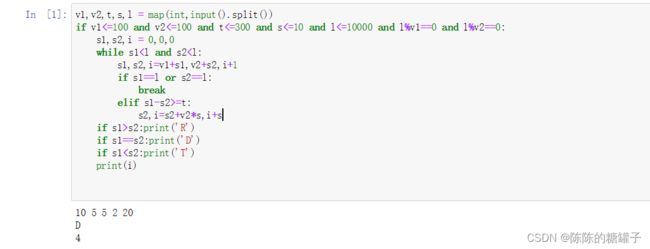
v1,v2,t,s,l = map(int,input().split())
if v1<=100 and v2<=100 and t<=300 and s<=10 and l<=10000 and l%v1==0 and l%v2==0:
    s1,s2,i = 0,0,0
    while s1<l and s2<l:
        s1,s2,i=v1+s1,v2+s2,i+1
        if s1==l or s2==l:
            break
        elif s1-s2>=t:
            s2,i=s2+v2*s,i+s
    if s1>s2:print('R')
    if s1==s2:print('D')
    if s1<s2:print('T')
    print(i)

2、芯片测试

有n（2≤n≤20）块芯片，有好有坏，已知好芯片比坏芯片多。
　　每个芯片都能用来测试其他芯片。用好芯片测试其他芯片时，能正确给出被测试芯片

是好还是坏。而用坏芯片测试其他芯片时，会随机给出好或是坏的测试结果（即此结果与

被测试芯片实际的好坏无关）。
　　给出所有芯片的测试结果，问哪些芯片是好芯片。
输入格式
　　输入数据第一行为一个整数n，表示芯片个数。
　　第二行到第n+1行为n*n的一张表，每行n个数据。表中的每个数据为0或1，在这n行

中的第i行第j列（1≤i, j≤n）的数据表示用第i块芯片测试第j块芯片时得到的测试结果，1

表示好，0表示坏，i=j时一律为1（并不表示该芯片对本身的测试结果。芯片不能对本身

进行测试）。
输出格式
　　按从小到大的顺序输出所有好芯片的编号

"""
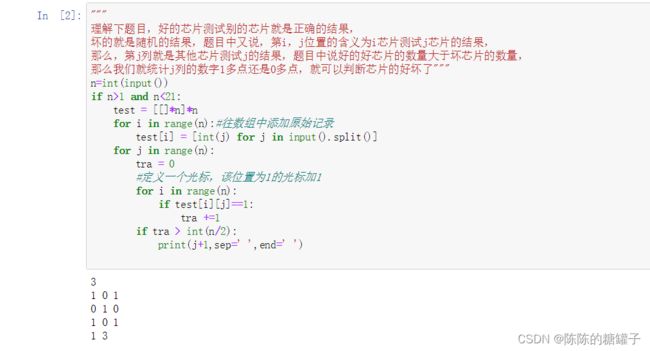
理解下题目，好的芯片测试别的芯片就是正确的结果，
坏的就是随机的结果，题目中又说，第i，j位置的含义为i芯片测试j芯片的结果，
那么，第j列就是其他芯片测试j的结果，题目中说好的好芯片的数量大于坏芯片的数量，
那么我们就统计j列的数字1多点还是0多点，就可以判断芯片的好坏了"""
n=int(input())
if n>1 and n<21:
    test = [[]*n]*n
    for i in range(n):#往数组中添加原始记录
        test[i] = [int(j) for j in input().split()] 
    for j in range(n):
        tra = 0
        #定义一个光标，该位置为1的光标加1
        for i in range(n):
            if test[i][j]==1:
                tra +=1
        if tra > int(n/2):
            print(j+1,sep=' ',end=' ')

3、FJ的字符串

问题描述
　　FJ在沙盘上写了这样一些字符串：
　　A1 = “A”
　　A2 = “ABA”
　　A3 = “ABACABA”
　　A4 = “ABACABADABACABA”
　　… …
　　你能找出其中的规律并写所有的数列AN吗？
输入格式
　　仅有一个数：N ≤ 26。
输出格式
　　请输出相应的字符串AN，以一个换行符结束。输出中不得含有多余的空格或换行、

回车符。
样例输入
3
样例输出
ABACABA

"""
完全二叉树思想＋递归
F1=A
A1=F1=A

F2=BF1=BA
A2=F1F2=ABA

F3=CF1F2=CABA
A3=F1F2F3=ABACABA
"""

def Tn(n):
    if n==1:
        print('A',end='')
    else:
        Tn(n-1)
        print(chr(65+n-1),end='')
        Tn(n-1)
    return ''

n=int(input())
Tn(n)

4、Sine之舞

An=sin(1–sin(2+sin(3–sin(4+…sin(n))…)
　　Sn=(…(A1+n)A2+n-1)A3+…+2)An+1
　　FJ想让奶牛们计算Sn的值，请你帮助FJ打印出Sn的完整表达式，以方便奶牛们做题。
输入格式
　　仅有一个数：N<201。
输出格式
　　请输出相应的表达式Sn，以一个换行符结束。输出中不得含有多余的空格或换行、回

车符。
样例输入
3
样例输出
((sin(1)+3)sin(1–sin(2))+2)sin(1–sin(2+sin(3)))+1

"""
A1=sin1
S1=A1+1=sin1+1

A2=sin(1-sin2)
S2=(A1+2)A2+1=(sin1+2)sin(1-sin2)+1

A3=sin(1-sin(2+sin(3)))
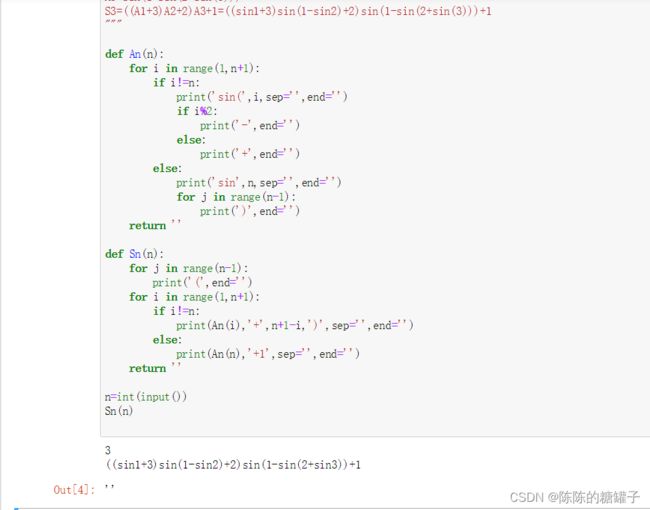
S3=((A1+3)A2+2)A3+1=((sin1+3)sin(1-sin2)+2)sin(1-sin(2+sin(3)))+1
"""

def An(n):
    for i in range(1,n+1):
        if i!=n:
            print('sin(',i,sep='',end='')
            if i%2:
                print('-',end='')
            else:
                print('+',end='')
        else:
            print('sin',n,sep='',end='')
            for j in range(n-1):
                print(')',end='')
    return ''
                
def Sn(n):
    for j in range(n-1):
        print('(',end='')
    for i in range(1,n+1):
        if i!=n:
            print(An(i),'+',n+1-i,')',sep='',end='')
        else:
            print(An(n),'+1',sep='',end='')
    return ''
            
n=int(input())
Sn(n)

5、数的读法

当他输入12 3456 7009时，会给出相应的念法：
　　十二亿三千四百五十六万七千零九
　　用汉语拼音表示为
　　shi er yi san qian si bai wu shi liu wan qi qian ling jiu

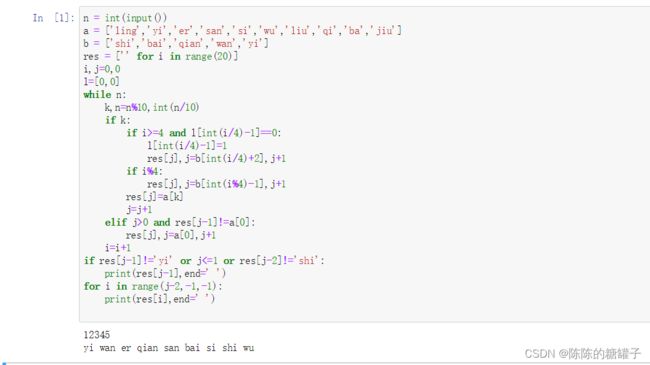
n = int(input())
a = ['ling','yi','er','san','si','wu','liu','qi','ba','jiu']
b = ['shi','bai','qian','wan','yi']
res = ['' for i in range(20)]
i,j=0,0
l=[0,0]
while n:
    k,n=n%10,int(n/10)
    if k:
        if i>=4 and l[int(i/4)-1]==0:
            l[int(i/4)-1]=1
            res[j],j=b[int(i/4)+2],j+1
        if i%4:
            res[j],j=b[int(i%4)-1],j+1
        res[j]=a[k]
        j=j+1
    elif j>0 and res[j-1]!=a[0]:
        res[j],j=a[0],j+1
    i=i+1
if res[j-1]!='yi' or j<=1 or res[j-2]!='shi':
    print(res[j-1],end=' ')
for i in range(j-2,-1,-1):
    print(res[i],end=' ')

6、完美的代价

给出一个字符串，不一定为回文，计算最少交换次数使得该字符串成为一个回文串。这里的交换定义是，交换两个相邻的字符。

例如mamad
　　第一次交换 ad : mamda
　　第二次交换 md : madma
　　第三次交换 ma : madam

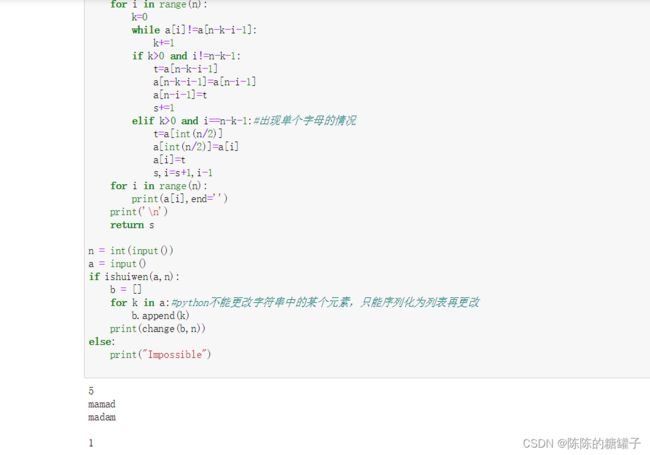
def ishuiwen(a,n):#判断是否能构成回文
    b = [' ' for i in range(26)]
    for i in range(26):
        b[i]=(chr(97+i))
        k=0
    for i in range(26):
        t=0
        for j in range(n):
            if b[i]==a[j]:
                t+=1
        if t%2!=0:
            k+=1
    if k>1:
        return 0
    else:
        return 1
def change(a,n):
    s=0
    for i in range(n):
        k=0
        while a[i]!=a[n-k-i-1]:
            k+=1
        if k>0 and i!=n-k-1:
            t=a[n-k-i-1]
            a[n-k-i-1]=a[n-i-1]
            a[n-i-1]=t
            s+=1
        elif k>0 and i==n-k-1:#出现单个字母的情况
            t=a[int(n/2)]
            a[int(n/2)]=a[i]
            a[i]=t
            s,i=s+1,i-1
    for i in range(n):
        print(a[i],end='')
    print('\n')
    return s

n = int(input())
a = input()
if ishuiwen(a,n):
    b = []
    for k in a:#python不能更改字符串中的某个元素，只能序列化为列表再更改
        b.append(k)
    print(change(b,n))
else:
    print("Impossible")

7、矩阵面积交

问题描述
　　平面上有两个矩形，它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形，我们

给出它的一对相对顶点的坐标，请你编程算出两个矩形的交的面积。
输入格式
　　输入仅包含两行，每行描述一个矩形。
　　在每行中，给出矩形的一对相对顶点的坐标，每个点的坐标都用两个绝对值不超过

10^7的实数表示。
输出格式
　　输出仅包含一个实数，为交的面积，保留到小数后两位。

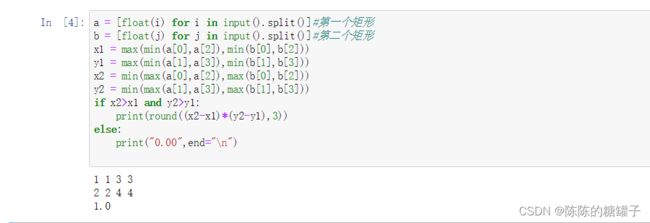
a = [float(i) for i in input().split()]#第一个矩形
b = [float(j) for j in input().split()]#第二个矩形
x1 = max(min(a[0],a[2]),min(b[0],b[2]))
y1 = max(min(a[1],a[3]),min(b[1],b[3]))
x2 = min(max(a[0],a[2]),max(b[0],b[2]))
y2 = min(max(a[1],a[3]),max(b[1],b[3]))
if x2>x1 and y2>y1:
    print(round((x2-x1)*(y2-y1),3))
else:
    print("0.00",end="\n")

8、矩阵乘法

问题描述
　　给定一个N阶矩阵A，输出A的M次幂（M是非负整数）
　　例如：
　　A =
　　1 2
　　3 4
　　A的2次幂
　　7 10
　　15 22
输入格式
　　第一行是一个正整数N、M（1<=N<=30, 0<=M<=5），表示矩阵A的阶数和要求的幂

数
　　接下来N行，每行N个绝对值不超过10的非负整数，描述矩阵A的值
输出格式
　　输出共N行，每行N个整数，表示A的M次幂所对应的矩阵。相邻的数之间用一个空格隔开

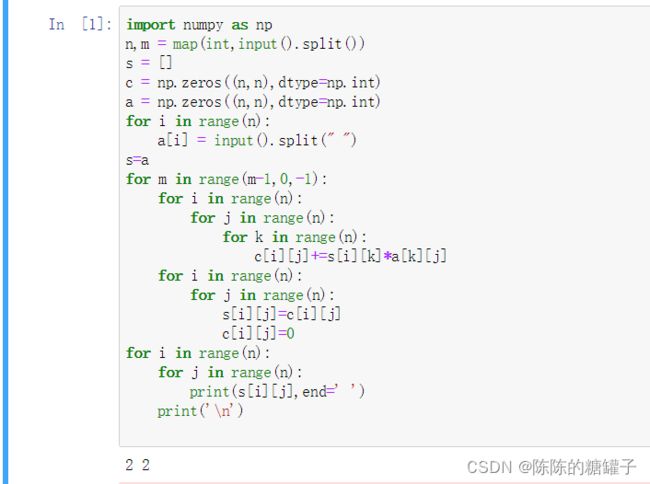
import numpy as np
n,m = map(int,input().split())
s = []
c = np.zeros((n,n),dtype=np.int)
a = np.zeros((n,n),dtype=np.int)
for i in range(n):
    a[i] = input().split(" ")
s=a
for m in range(m-1,0,-1):
    for i in range(n):
        for j in range(n):
            for k in range(n):
                c[i][j]+=s[i][k]*a[k][j]
    for i in range(n):
        for j in range(n):
            s[i][j]=c[i][j]
            c[i][j]=0
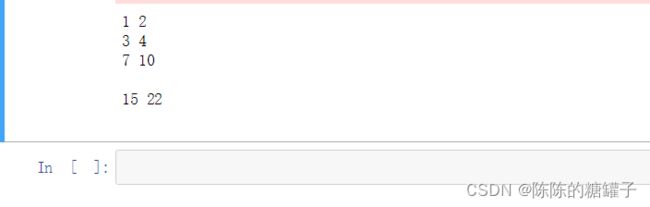
for i in range(n):
    for j in range(n):
        print(s[i][j],end=' ')
    print('\n')