python多项式回归预测(基于淘宝双十一数据)
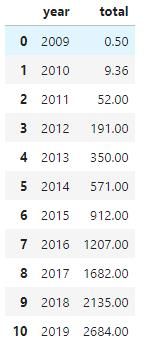
双11已经结束,按照天猫官方公布的最终数据看,今年的双11成交额为2684亿元,成功刷新了自己创下的商业纪录。然而,早在2019年4月就有网友指出,从天猫双十一的全天销售额来看,实际生产数据几乎完美地分布在三次回归曲线上,拟合度均超过99.94%,几乎为1,而且生产数据有10年之久,每一年的数据都这么高度拟合,数据过于完美。与此同时,这名网友还预测,“2019年淘宝双11当天的销售额为2675.37亿或2689.00亿。”,而这一预测,也因为贴合天猫今年的双十一最终交易数据,而被认为是神预测。
针对这一内容,天猫相关负责人此前也回应称,“按照网友的逻辑,符合统计趋势的就是假的。那么,世界经济总量也是能被预测的,经济发展也是假的吗?自己YY下满足自嗨就算了,由此得出天猫双11数据造假,就是造谣了哦,要负法律责任的!”
咱们且不论天猫数据有没有造假,今天我们通过这个案例中数据,利用python进行多项式回归的训练,学习一下多项式回归,顺便看看天猫的数据到底有多么‘完美’。
一.首先看一下天猫数据的‘庐山真面目’
# 1 用 Pandas 加载数据集
import pandas as pd
from matplotlib import pyplot as plt
df = pd.read_excel("E:\\job\\tmall.xlsx",header=0)
#df
# 2 绘制趋势图像
# 从原数据集中分离出需要的数据集(DataFrame)
x = df['year']
y = df['total']
# 绘图
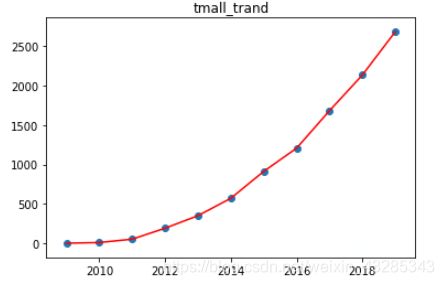
plt.plot(x, y, 'r')
plt.scatter(x, y)
plt.title('tmall_trand')二.二次多项式回归预测
# 3 训练集和测试集划分
# 将2009-2018年的数据定义为训练集,2010-2019年的数据定义为测试集
train_df = df[:int(len(df)*0.95)]
test_df = df[int(len(df)*0.05):]
# 定义训练和测试使用的自变量和因变量
train_x = train_df['year'].values
train_y = train_df['total'].values
test_x = test_df['year'].values
test_y = test_df['total'].values
# 4. 二次多项式预测
from sklearn.preprocessing import PolynomialFeatures
# 二次多项式回归特征矩阵
poly_features_2 = PolynomialFeatures(degree=2, include_bias=False)
poly_train_x_2 = poly_features_2.fit_transform(train_x.reshape(len(train_x),1))
poly_test_x_2 = poly_features_2.fit_transform(test_x.reshape(len(test_x),1))
# 二次多项式回归模型训练与预测
model = LinearRegression()
model.fit(poly_train_x_2, train_y.reshape(len(train_x),1)) # 训练模型
results_2 = model.predict(poly_test_x_2) # 预测结果
results_2.flatten() # 打印扁平化后的预测结果
print("二次多项式2019年预测值为: ", results_2[-1])
print("二次多项式回归平均绝对误差: ", mean_absolute_error(test_y, results_2.flatten()))
print("二次多项式均方根误差: ", mean_squared_error(test_y, results_2.flatten()))
# 绘出已知数据散点图
#plt.scatter(x,y,color = 'blue')
plt.plot(x,y,color = 'blue',linewidth = 2)
# 绘出预测线
plt.plot(test_x,results_2,color = 'red',linewidth = 2)
plt.title('Predict the tmall total')
plt.xlabel('year')
plt.ylabel('total')
plt.show()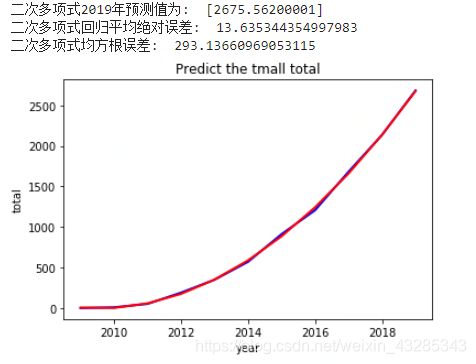
可见,天猫双十一销售总额用二次多项式预测的结果为2675.56亿,与‘质疑淘宝数据造假’的网友的结论基本一致。而且可以看出淘宝的数据确实和二次多项式函数值极度吻合(上图中蓝色线为实际成交额曲线和红色线为预测的二次多项式曲线,两者基本完全重合)。这样的经营数据确实是可遇而不可求啊!
三.多项式预测的次数到底如何选择
在选择模型中的次数方面,可以通过设置程序,循环计算各个次数下预测误差,然后再根据结果反选参数。
# 多项式回归预测次数选择
# 计算 m 次多项式回归预测结果的 MSE 评价指标并绘图
from sklearn.pipeline import make_pipeline
train_df = df[:int(len(df)*0.95)]
test_df = df[int(len(df)*0.95):]
# 定义训练和测试使用的自变量和因变量
train_x = train_df['year'].values
train_y = train_df['total'].values
test_x = test_df['year'].values
test_y = test_df['total'].values
train_x = train_x.reshape(len(train_x),1)
test_x = test_x.reshape(len(test_x),1)
train_y = train_y.reshape(len(train_y),1)
mse = [] # 用于存储各最高次多项式 MSE 值
m = 1 # 初始 m 值
m_max = 10 # 设定最高次数
while m <= m_max:
model = make_pipeline(PolynomialFeatures(m, include_bias=False), LinearRegression())
model.fit(train_x, train_y) # 训练模型
pre_y = model.predict(test_x) # 测试模型
mse.append(mean_squared_error(test_y, pre_y.flatten())) # 计算 MSE
m = m + 1
print("MSE 计算结果: ", mse)
# 绘图
plt.plot([i for i in range(1, m_max + 1)], mse, 'r')
plt.scatter([i for i in range(1, m_max + 1)], mse)
# 绘制图名称等
plt.title("MSE of m degree of polynomial regression")
plt.xlabel("m")
plt.ylabel("MSE")

从误差结果可以看到,次数取二及以上误差基本稳定,没有明显的减少了,考虑到模型的泛化能力,避免出现过拟合,这里就可以选择 二次多项式为最优回归预测模型。
All things are difficult before they are easy.