LeetCode 剑指 Offer II 动态规划（四） 专题总结

往期文章 ：

• LeetCode 剑指 Offer II 回溯(上) 专题总结
• LeetCode 剑指 Offer II 回溯(下) 专题总结
• LeetCode 剑指 Offer II 动态规划（一） 专题总结
• LeetCode 剑指 Offer II 动态规划（二） 专题总结
• LeetCode 剑指 Offer II 动态规划（三） 专题总结

后两道都是0-1背包问题

100. 三角形中最小路径之和

题目：

给定一个三角形 triangle ，找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

提示：

• 1 <= triangle.length <= 200
• triangle[0].length == 1
• triangle[i].length == triangle[i - 1].length + 1
• -104 <= triangle[i][j] <= 104

思路：

将三角形看成直角三角形，左下角为直角
当前行下标为i，可以由上一行下标i-1或i移动得到最小路径和
动态规划方程：
f[i][j] = min(f[i-1][j-1], f[i-1][j]) + triangle[i][j];
可以优化成一维数组,第二层循环从后往前更新，否则前面值会将上一层值替换掉
一维动态规划：
f[j] = min(f[j-1], f[j]) + triangle[i][j];

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int n = triangle.size();
        int m = n; // 最底层列数
        vector<int> dp(m, 0);
        for(int i = 0; i < n; i++) {
            for(int j = i; j >= 0; j--) {
                if(j == 0) {
                    dp[0] += triangle[i][j];
                    continue;
                }
                if(j == i) {
                    dp[j] = dp[j-1] + triangle[i][j];
                    continue;
                }
                dp[j] = min(dp[j-1], dp[j]) + triangle[i][j];
            }
        }
        return *min_element(dp.begin(), dp.end());
    }
};

101. 分割等和子集

题目：

给定一个非空的正整数数组 nums ，请判断能否将这些数字分成元素和相等的两部分。

示例：

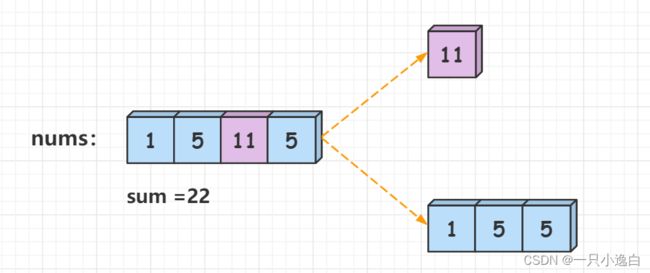
输入：nums = [1,5,11,5]
输出：true
解释：nums 可以分割成 [1, 5, 5] 和 [11] 。

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

思路：

样例：

如样例所示，nums = [1,5,11,5]，数组可以分割成 [1, 5, 5] 和 [11]，这两个子集各自的数字和都等于整个数组的元素和的一半，因此返回ture。
最骚的是官方这段前言，可以期待一下图灵奖了
本题是经典的「NP 完全问题」，也就是说，如果你发现了该问题的一个多项式算法，那么恭喜你证明出了 P=NP，可以期待一下图灵奖了。
正因如此，我们不应期望该问题有多项式时间复杂度的解法。我们能想到的，例如基于贪心算法的「将数组降序排序后，依次将每个元素添加至当前元素和较小的子集中」之类的方法都是错误的，可以轻松地举出反例。因此，我们必须尝试非多项式时间复杂度的算法，例如时间复杂度与元素大小相关的动态规划。
————————————————————————————————————————————————————————————
0 - 1 背包问题
该问题的本质就是，能否从数组中选出若个数字，使它们的和等于 target = sum / 2，每个数组取一次，所以可以转化成01背包问题。
设 f(i, j) 表示能否从前 i 个物品(物品编号为 0 ~ i - 1)中选择若干物品放满容量为 j 的背包。对于 f(i, j) 存在两个选择，第一个选择是将标号为 i - 1 的物品放入背包，如果能从前 i - 1 个物品中选择若干物品放满容量为 j - nums[i - 1] 的背包(即 f(i - 1, j - nums[i - 1]) 为 true)，那么 f(i, j) 为 true。另一个选择是不把标号为 i - 1 的物品放入背包，如果能从前 i - 1 个物品中选择若干物品放满容量为 j 的背包(即 f(i - 1, j) 为 true)，那么 f(i, j) 为 true。即

当 j 等于 0 时，即背包容量为空，只要不选择物品就可以，所以 f(i, 0) 为 true。当 i 等于 0 时，即物品数量为 0，那么除了空背包都无法装满，所以当 j 大于 0 时，f(0, j) 为 fasle;

二维数组

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int n = nums.size();
        int sum = 0, maxNum = 0;
        for(auto& num : nums) {
            sum += num;
            maxNum = max(maxNum, num);
        }
        int target = sum / 2;
        if(sum & 1 || target < maxNum) {
            return false;
        }
        vector<vector<bool>> dp(n, vector<bool>(target+1, false));
        for(int i = 0; i < n; i++) {
            dp[i][0] = true;
        }
        dp[0][nums[0]] = true;
        for (int i = 1; i < n; i++) {
            for (int j = 1; j <= target; j++) {
                if (j >= nums[i]) {
                    dp[i][j] = dp[i - 1][j] | dp[i - 1][j - nums[i]];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[n-1][target];
    }
};

在使用二维矩阵的时候可以发现，当前行其实是在前一行的基础上进行更新的，所以使用一维的数组可以无需复制前一行的数据直接更新，这样会更高效。但是要注意 j 是从大往小遍历，因为这样不会破坏之前的值。

一维数组

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int n = nums.size();
        int sum = 0, maxNum = 0;
        for(auto& num : nums) {
            sum += num;
            maxNum = max(maxNum, num);
        }
        int target = sum / 2;
        if(sum & 1 || target < maxNum) {
            return false;
        }
        vector<bool> dp(target, false);
        dp[0] = true;
        for (int i = 1; i < n; i++) {
            for (int j = target; j >= nums[i]; j--) {
                dp[j] = dp[j] | dp[j - nums[i]];
            }
        }
        return dp[target];
    }
};

102. 加减的目标值

题目：

给定一个正整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ，然后串联起所有整数，可以构造一个 表达式 ：

• 例如，nums = [2, 1] ，可以在 2 之前添加 ‘+’ ，在 1 之前添加 ‘-’ ，然后串联起来得到表达式 “+2-1” 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例：

输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

提示：

• 1 <= nums.length <= 20
• 0 <= nums[i] <= 1000
• 0 <= sum(nums[i]) <= 1000
• -1000 <= target <= 1000

思路：

0 - 1 背包问题
题目中明确数组内所有的数字都为正数，如果把所有取正号的数字之和记为 p，剩下的取负号的数字之和记为 q，若存在符合题意的组合则 p - q = target，同时记所有的数字之和为 p + q = sum。将以上两式相加得 p = (target + sum) / 2。因此，这个问题就等价于计算从数组中选出和为 (target + sum) / 2 的数字的方法的数目。
设 f(i, j) 为在数组的前 i 个数字中选出若干个数字使其和等于 j 的方法的数目。这个状态转移方程面试题 101 非常相似。状态转移方程为
因为 0-1 背包问题很适合使用一维数组，所以直接给出一维数组的完整程序。

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = 0;
        for (auto& n : nums) {
            sum += n;
        }
        if ((target + sum) & 1 != 0 || sum < target) {
            return 0;
        }
         
        vector<int> dp((target + sum) / 2 + 1, 0);
        dp[0] = 1;
        for (auto& n : nums) {
            for (int j = dp.size() - 1; j >= n; --j) {
                dp[j] += dp[j - n];
            }
        }
        return dp.back();
    }
};