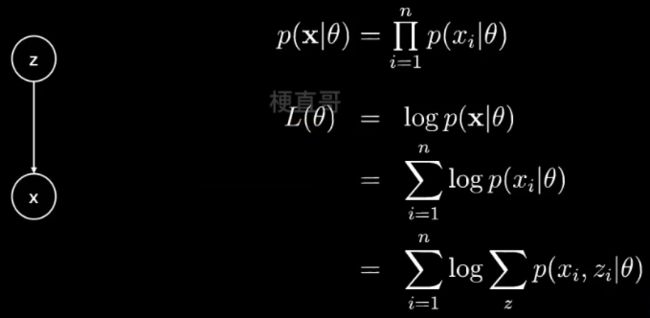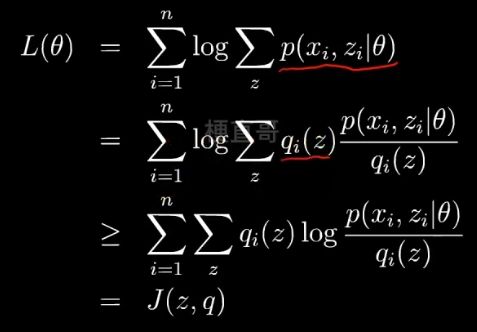机器学习 | 概率图模型

        见微知著，睹始知终。

        见到细微的苗头就能预知事物的发展方向，能透过微小的现象看到事物的本质，推断结论或者结果。

        概率模型为机器学习打开了一扇新的大门，将学习的任务转变为计算变量的概率分布。

        实际情况中，各个变量间存在显式或隐式的相互依赖，如朴素贝叶斯方法直接基于训练数据去求解变量的联合概率分布在时间复杂度还是空间复杂度均是不可行、不划算的。

        直接基于训练数据求解变量联合概率分布困难。

        Probabilistic Graphical Model，简称PGM，就是用图来表示变量概率间的依赖关系。

        

        概率图模型可以简单的理解为 概率 + 图（结构）

        它不仅可以刻画各个变量间的概率关系，还可以进行高效的推理。

        结点表示随机变量，边表示变量间概率关系（一般是条件概率分布）

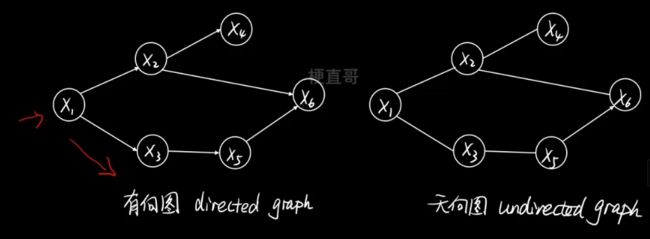
        根据边是否有指向，分为有向图和无向图。

        有向图可以显示的刻画变量间的因果（生成）关系。

        无向图表示的只是一种关联关系或者说是相关关系。

        

---

 1、核心思想及原理

        概率图模型主要步骤

                1、表示 Reprcntation ，将实际问题建模成某种图结构

                2、推断 lnference，计算感兴趣的图节点的后验概率分布

                3、学习 Learning，估计模型参数

        通过第一步计算可以得到全体节点随机变量的联合概率分布，

        我们的目的

        是分析部分目标节点变量或者说根据一些观测到的数据求另外一些的变量，

        用数学的语言来说就是 计算节点变量的条件概率分布和边际概率分布。

        

        整体上求解他们的过程就是推断。

        边际概率分布其实就是把其中一些不需要的变量通过求和或积分消去。

        学习的过程就是参数估计的过程，通常使用最优化方法MLE或MAP求解。

        

        但如果把参数也当成要去推测的变量，也算作一些节点，男参数估计就可以认为是推断的一部分，

        所以一些书籍中也把推断和学习的过程统一为推断。

1.1、表示 —— 有向图 （也叫贝叶斯网络）

        在结构上是一个网络，在概率分布上符合贝叶斯公式。可以表示任何的概率分布。

        节点对应连续或离散随机变量。

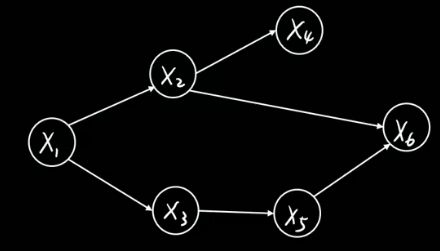
        有向边连接父子节点。从 xi指向xj，xi 就是父节点，xj 就是子节点。

        有向边表示条件概率分布。

        比如下图中，从x2指向x4的边就可以表示为 p (x4 | x2)，先有爹才能有儿子。

       图中不存在任何回路，又称为有向无环图模型。Directed Acyclic Graph，DAG。

        

        一个概率图模型中的联合概率分布可以由概率中的乘法公式展开：

        理论上只有父母有用。

        

        比如：

        

        

        之前学过的各种模型，比如线性模型、神经网络都可以看成有向图模型，

        他就像贝叶斯方法一样，在某种程度上把前面的所有模型在方法论层面高度统一到了一个框架下。

---

1.2、表示 —— 无向图（又叫马尔可夫网络 / 马尔可夫随机场）

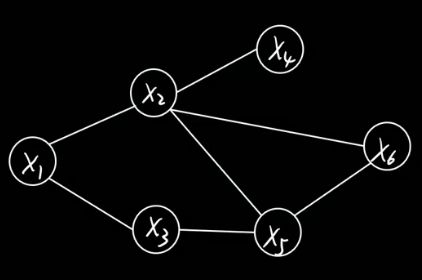
        节点对应连续或离散随机变量。

        边表示依赖关系。

        任意两节点间都有边连接，则该节点子集为团clique，比如下图中的x2 x5 x6。

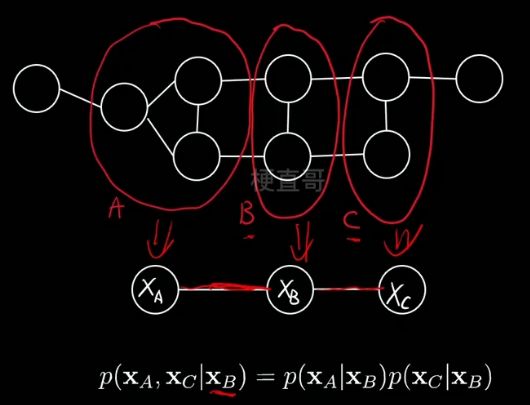
        联合概率分布能基于团分解.

        

        下例中，也就是说在给定xb的情况下，xa和xc就条件独立了。可以大大简化计算。

        

         用数学语言来表示 所有节点的联合概率分布：

        

        Q 表示某一个团，C是所有团的总称，

        后面是团Q对应的势函数（一个概率分布，团伙的势力/影响力）

        Z 归一化因子，确保整体求完还是一个概率，实际很难算，多数情况下只需要最优化求模型参数就可以，Z就类似于一个常数，所以不太需要

        之所以这么分解的原因是要更好地利用条件独立，也就是马尔可夫性质。

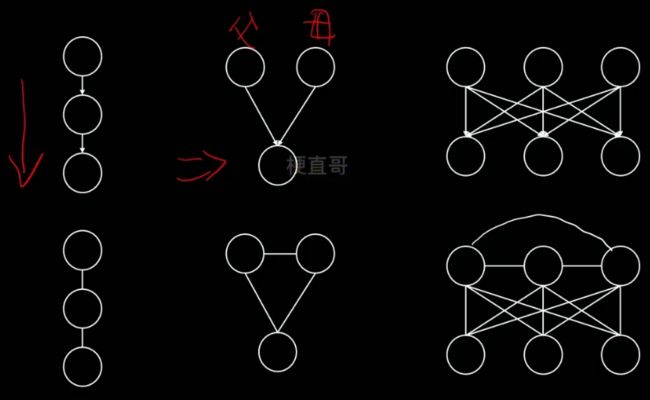
有向图转无向图（也叫道德化）

        

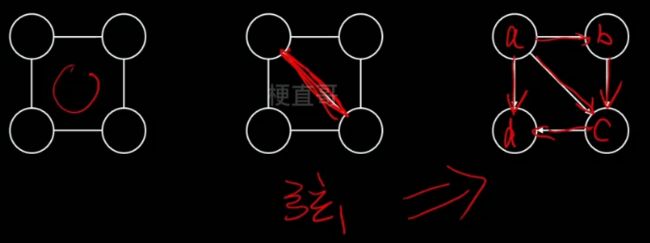
无向图转有向图

         也分为两个步骤：

                1、含有环状的结构三角化

                2、弦图加箭头，箭头方向可以对节点的随机变量排序，较早的指向叫晚的

        下图中间一张也叫弦图。

        

---

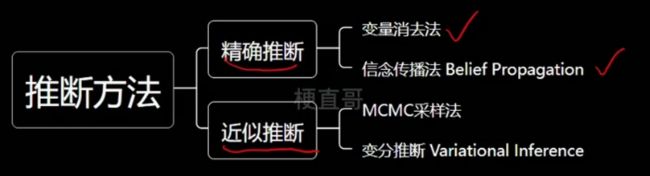
1.3、推断

        精确推断法，比较理想，实际中很难实现。

        重点掌握近似推断。

        

        MCMC主要思想：

                在很多时候我们关心的并不是概率分布本身而是他们的期望，根据这些期望做出决策。

                去估计概率分布本身比较困难，就直接计算或逼近期望值。

        变分推断主要思想：

                通过使用已知的简单分布逼近需要推断的复杂分布。

---

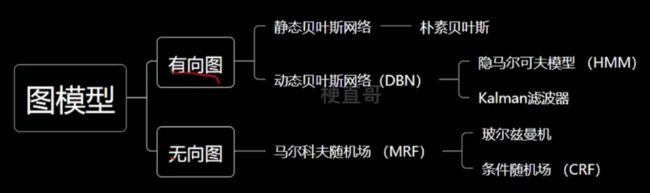
 1.4、概率图模型家族

        

---

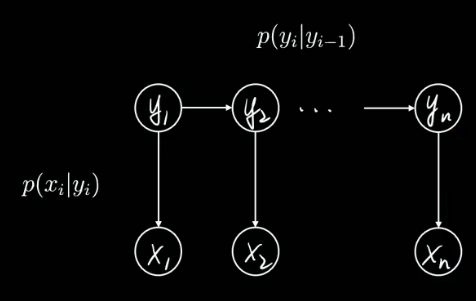
1.5、隐马尔科夫模型 Hidden Markov Model

        假设有一系列的状态变量 yi，生成了一堆观测xi，

        n可以是不同时间或先后顺序，’比如语音识别中就是时间先后，nlp分析中就是词的先后顺序，

        我们听到的声音或者看到的文字就是观测。背后其实是有真实状态的。

        数学上就是条件概率分布（也叫likelihood，贝叶斯公式中的似然函数），

        因为状态未知，所以认为是隐藏的，又因为有先后顺序，就用一条有方向的链表示，

        节点与节点之间符合马尔可夫性质，节点之间的关系就可以简化，就是隐马尔可夫链。

        

---

 2、近似推断 EM算法参数估计

        期望最大化算法，Expectation Maximization

        概率图模型都可以简化为有两个节点的有向图：

                 z 是隐变量，x 是观测变量，箭头表示生成关系。

                这两个节点本身也可以是向量，可以是一个集合，包含其他很多变量（节点）。

        z 虽然未知，但是可以假定它含有一系列参数 θ，

        观测 x 也满足一个带有参数 θ 的分布。

        给定观测数据 x ，假定有 n 个样本，现在想要估计参数 θ 就可以：

                最大化 似然函数 p（ x | θ ）。

        假定 n 个样本是条件独立的，因为我们不太喜欢连乘，所以加上 log 运算，就变成了求和。

        继续展开，引入隐变量 z ，就可以得到 每个样本每种可能的类别 z ，求联合概率分布之和。

                z 如果是个已知的数，很容易用极大似然法求出 θ，

                但现在 z 是隐变量，就用要 EM算法 近似推断。

                注：那可以使用梯度下降法吗？

                        可以，但是当z过多时，求梯度时运算就会指数级的上升，EM效率更高。

        z 是一个因变量，那该怎么求 x 和 z 的联合概率分布函数呢？

        

EM算法思想

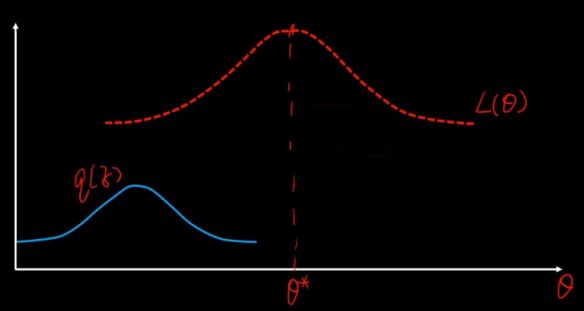
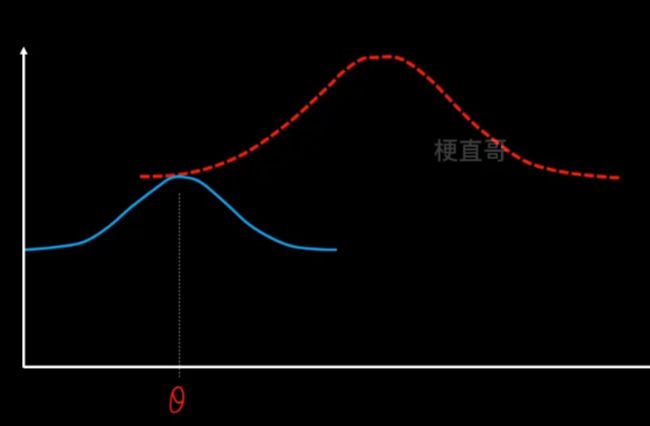
        目的：使得似然函数最大化

        先猜一个 z 的分布，就是蓝色的分布，然后用它来逼近。

        

        

        利用Jensen不等式：期望的函数 ≥ 函数的期望，

        函数就是log函数，后面的一坨是期望，把q看成一个分布 分式看成z的函数。

        现在就可以通过不断改变 z，q来搜索L(θ)，从而找到他的最大值。

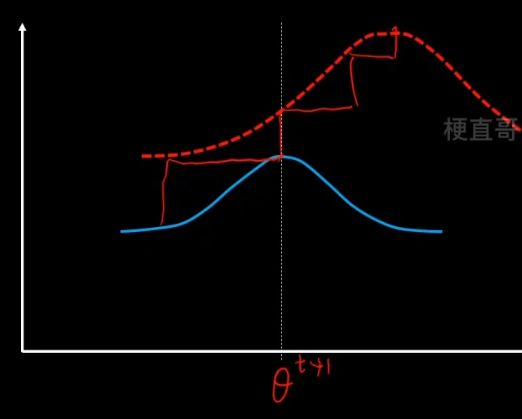
EM算法步骤

        1、E步骤，先固定q分布不变（θ值不变），使用MLE来最大化z。

                沿着固定的θ值，向上搜索，碰到红线之后就停止。

                

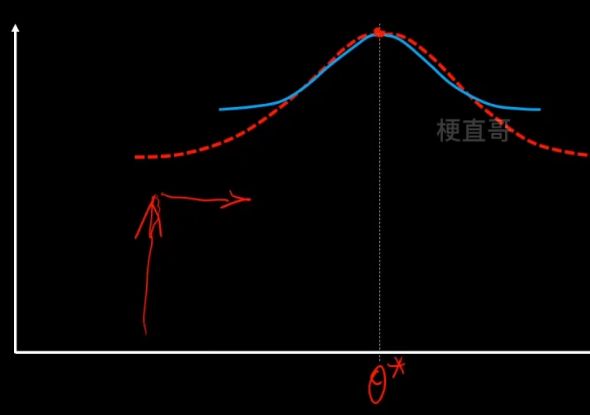
        2、M步骤，固定z不变，让q最大化寻优。

                

                重复这个步骤，反复迭代，直到找到最优的θ*。

                

                 注意虽然EM的迭代一定会收敛，但是不一定收敛到最优的参数值，可能陷入局部最优，所以结果很受初始值的影响。

                

---

3、隐马尔可夫模型代码实现

         对序列数据进行建模的有效办法。

        隐马尔可夫模型对问题进行了简化，有两大基本假设：

                1、任意时刻的观测只依赖于该时刻的马尔科夫链的状态，与其他的观测以及状态没有关系。

                2、t 时刻的状态只与 t-1 时刻的状态有关，与其他时刻的状态和观测都无关。

                

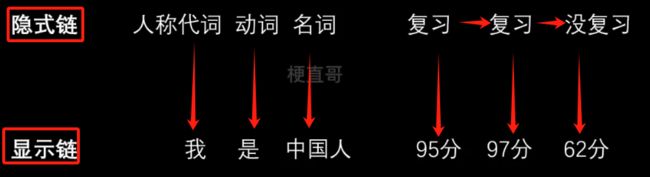
马尔可夫链 / 隐马尔可夫模型链

        隐式链通常是一个状态的链。

        

简单的隐马模型

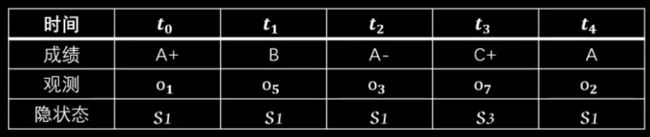
        Example：

        假设观测有9个等级，分别对应

        状态有三种，假定保持状态不变的概率是0.4，三种状态之间互相转换的概率是0.3。

        

建模 —— 隐马模型三要素

        发射概率矩阵，描述了在每种隐藏状态下发生观测值的概率。（就是可能性 / 似然函数）

        

         现在我们就可以根据考试成绩序列 o 来推断出状态序列 s 的最大可能性了。

         现在假设五次考试成绩如下：

        

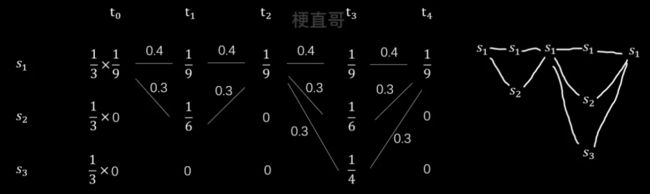
        1、首先根据发射概率矩阵列出每个时刻每种状态的概率。

        2、用连线绘制出状态转移的情况。

        3、因为 t0 时刻不涉及状态转移，所以要乘初始概率。

         

        从前往后分析，

                先来看 t1 时刻，有两个状态，s1对应的概率为 0.4 x 1/9，s2对应的概率为0.3 x 1/6

                再看 t2 时刻，只有一个状态 s1，但第一条路线概率为 0.4x1/9+0.4x1/9 大于第二条路线 0.3x1/6+0.3x1/9，所以选择第一条路线。

                同理，得到最终结果：

                

        上述计算隐藏状态序列的方法就是维特比算法，是隐马模型最常用的解码方法。

---

代码实现：
        hmmlearn —— CategoricalHMM
能力：

        预测隐藏状态序列

        预测观测序列概率

        生成条件约束数据

数据准备

import numpy as np
state = np.array(['认真复习', '简单复习', '没有复习'])
grade = np.array(['A+', 'A', 'A-', 'B+', 'B', 'B-', 'C+', 'C', 'C-'])
n_state = len(state)
m_grade = len(grade)
pi = np.ones(n_state)/n_state
t = np.array([
    [0.4, 0.3, 0.3],
    [0.3, 0.4, 0.3],
    [0.3, 0.3, 0.4]
])
e = np.zeros([3,9])
e[0, :9]=1/9
e[1, 3:9]=1/6
e[2, 5:9]=1/4

print("初始概率矩阵：\n",pi)
print("转移矩阵：\n",t)
print("发射矩阵：\n",e)

初始概率矩阵：
 [0.33333333 0.33333333 0.33333333]
转移矩阵：
 [[0.4 0.3 0.3]
 [0.3 0.4 0.3]
 [0.3 0.3 0.4]]
发射矩阵：
 [[0.11111111 0.11111111 0.11111111 0.11111111 0.11111111 0.11111111
  0.11111111 0.11111111 0.11111111]
 [0.         0.         0.         0.16666667 0.16666667 0.16666667
  0.16666667 0.16666667 0.16666667]
 [0.         0.         0.         0.         0.         0.25
  0.25       0.25       0.25      ]]

---

hmmlearn

pip install hmmlearn

Looking in indexes: http://mirrors.tencentyun.com/pypi/simple
Requirement already satisfied: hmmlearn in /home/ubuntu/.local/lib/python3.8/site-packages (0.2.8)
Requirement already satisfied: scikit-learn>=0.16 in /home/ubuntu/.local/lib/python3.8/site-packages (from hmmlearn) (1.1.2)
Requirement already satisfied: scipy>=0.19 in /usr/local/lib/python3.8/dist-packages (from hmmlearn) (1.8.0)
Requirement already satisfied: numpy>=1.10 in /usr/local/lib/python3.8/dist-packages (from hmmlearn) (1.22.2)
Requirement already satisfied: threadpoolctl>=2.0.0 in /home/ubuntu/.local/lib/python3.8/site-packages (from scikit-learn>=0.16->hmmlearn) (3.1.0)
Requirement already satisfied: joblib>=1.0.0 in /home/ubuntu/.local/lib/python3.8/site-packages (from scikit-learn>=0.16->hmmlearn) (1.1.0)
Note: you may need to restart the kernel to use updated packages.

from hmmlearn.hmm import CategoricalHMM
hmm = CategoricalHMM(n_state)

 此处我们选择适于离散值的categoricalHMM。

hmm.startprob_ = pi
hmm.transmat_ = t
hmm.emissionprob_ = e
hmm.n_feature = 9  #观测值个数

 因为HMM接受的参数是二维的，所以进行升维操作。

datas = np.array([0, 4, 2, 6, 1])
datas = np.expand_dims(datas, axis=1)
states = hmm.predict(datas)

states

array([0, 0, 0, 2, 0])

预测一下出现观测值的概率 ：

prob = hmm.score(datas)
prob

-14.003674820375014

这是取 In 之后的结果。

print(np.exp(prob))

8.284786081615825e-07

 因为每种观测值可能性是无限的，随着观测序列的加长，概率越来越低。

 生成满足三要素约束的数据：

datas , states = hmm.sample(10000)

 验证是否满足约束：

t_2 = np.zeros([3,3])
for i in range(3):
    current = np.where(states == i)[0]
    next_index = current+1
    next_index = next_index[:-1]

    tmp = states[next_index]
    for j in range(3):
        t_2[i][j] = np.where(tmp==j)[0].shape[0]/np.shape(tmp)[0]
print(t_2)

[[0.41121495 0.29333735 0.29544769]
 [0.28884285 0.40988458 0.30127257]
 [0.29627386 0.30930021 0.39442593]]

e_2 = np.zeros([3,9])
for i in range(3):
    current = np.where(states == i)[0]
    next_index = current+1
    next_index = next_index[:-1]
    tmp = datas[current]
    for j in range(9):
        e_2[i][j] = np.where(tmp==j)[0].shape[0]/np.shape(tmp)[0]
print(e_2)

[[0.10518385 0.10066305 0.11030741 0.11603376 0.11000603 0.1106088
  0.12115732 0.12085594 0.10518385]
 [0.         0.         0.         0.1760355  0.15591716 0.16242604
  0.17071006 0.16952663 0.16538462]
 [0.         0.         0.         0.         0.         0.24863719
  0.25741975 0.24500303 0.24894004]]

---

 4、模型优缺点及发展方向

        

HMM算法优缺点

        建立在一阶马尔可夫假设和观测独立假设之上。

        很多场景下可以大大简化条件概率计算。

        应用范围比较窄，主要用于时序数据建模。

概率图模型优缺点

        不管问题复杂与否，处理思路都是：建模表示 + 推断学习，用图结构来表示，计算概率分布，然后进行推断和学习。对于复杂实际问题，特别是大型的人工智能系统来说是很有价值的，因为图模型中每个变量都有明确的解释，变量之间可以依赖专家或人工定义。所以可解释性强，相当于一个白盒字模型。

        如何确定节点间拓扑关系，如何高效的进行推断和学习未知。

        推断和学习复杂，高维数据处理困难。

       

概率图模型发展方向

        动态化结构学习是概率图模型发展的一个方向。

        非参数话建模是概率图模型可能的重要方向。

        深度学习擅长感知类的任务，但不擅长推理和推断任务，深度学习和概率图结合也是未来发展的重要方向。

---

参考

机器学习必修课：经典算法与编程实战 梗直哥瞿炜_哔哩哔哩_bilibili

Chapter-14/14-4 隐马尔可夫模型代码实现.ipynb · 梗直哥/Machine-Learning - Gitee.com