如何使用自动编码器生成图像
How to Generate Images using Autoencoders
你知道什么会很酷吗?如果我们不需要所有那些标记数据来训练我们的模型。我的意思是标记和分类数据需要太多的工作。不幸的是,从支持向量机到卷积神经网络的大多数现有模型如果没有它们就无法进行训练。
除了一小组算法,他们可以。好奇?这就是所谓的无监督学习。无监督学习通过自己的无标签数据推断出一个函数。最着名的无监督算法是K-Means,它已被广泛用于将数据聚类成组和PCA,这是降维的解决方案。 K-Means和PCA可能是有史以来最好的两种机器学习算法。让他们变得更好的是他们的简单。我的意思是,如果你掌握它们,你就会像:“我为什么不早点想到它?”
我们想到的下一个问题是:“是否存在无监督的神经网络? “。你可能知道帖子标题的答案。自动编码。
为了更好地理解自动编码器,我将在解释的同时提供一些代码。请注意,我们将使用Pytorch来构建和训练我们的模型。
import torch
from torch import nn, optim
from torch.autograd import Variable
from torch.nn import functional as F
自动编码器是简单的神经网络,它们的输出是它们的输入。 就那么简单。 他们的目标是学习如何重建输入数据。 但它有什么用呢? 诀窍是他们的结构。 网络的第一部分就是我们所说的编码器。 它接收输入并将其编码在较低维度的潜在空间中。 第二部分(解码器)采用该向量并对其进行解码以生成原始输入。
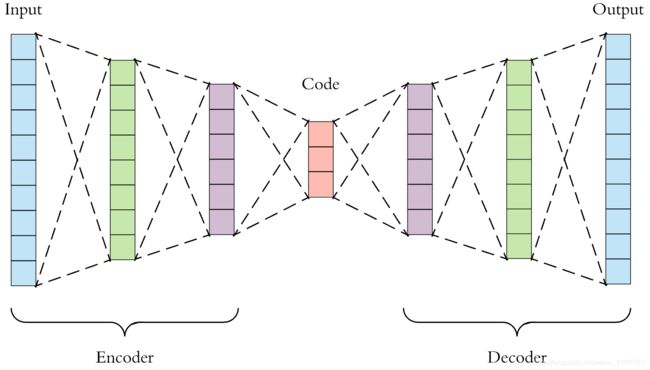
中间的潜在向量是我们想要的,因为它是输入的压缩表示。应用程序非常丰富,例如:
-
压缩
-
降维
此外,很明显,我们可以应用它们来重现相同但有点不同甚至更好的数据。例如:
-
数据去噪:用嘈杂的图像输入它们并训练它们输出相同的图像但没有噪声
-
训练数据增加
-
异常检测:在一个类上训练它们,以便每个异常都会产生很大的重建错误。
然而,自动编码器面临与大多数神经网络相同的几个问题。他们往往过度适应,他们遭受消失的梯度问题。有解决方案吗?变分自动编码器是一个非常好的和优雅的努力。它本质上增加了随机性但不完全相同。
让我们进一步解释一下。变分自动编码器经过训练,可以学习模拟输入数据的概率分布,而不是映射输入和输出的函数。然后,它从该分布中采样点并将它们馈送到解码器以生成新的输入数据样本。但是等一下。当我听说概率分布时,只有一件事物浮现在脑海中:贝叶斯。是的,贝叶斯规则再次成为主要原则。顺便说一句,我并不是夸大其词,但贝叶斯公式是有史以来最好的方程式。而且我不是在开玩笑。无处不在。如果您不知道是什么,请查阅。放弃那篇文章,了解贝叶斯是什么。我会原谅你的。
回到变分自动编码器。我认为以下图像清晰起来:
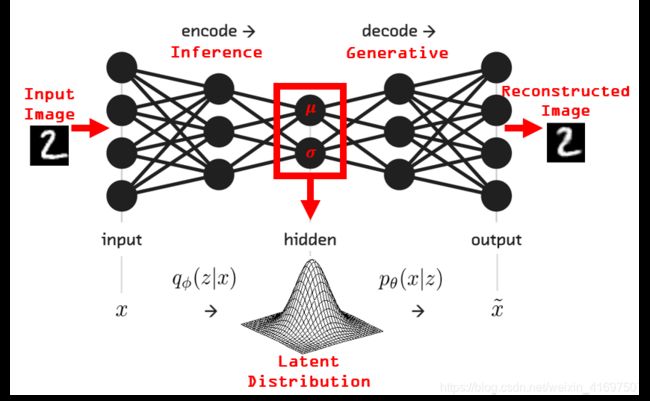
你有它。 随机神经网络。 在我们构建一个生成新图像的示例之前,讨论更多细节是合适的。
VAE的一个关键方面是损失功能。 最常见的是,它由两部分组成。 重建损失测量重建数据与原始数据的不同程度(例如二进制交叉熵)。 KL-分歧试图使过程正规化并使重建数据尽可能多样化。
def loss_function(recon_x, x, mu, logvar) -> Variable:
BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784))
KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
KLD /= BATCH_SIZE * 784
return BCE + KLD
另一个重要方面是如何训练模型。 难以发生,因为变量是注释确定性的,但随机和梯度下降通常不会那样工作。 为解决这个问题,我们使用重新参数化。 潜在向量(z)将等于我们分布的学习平均值(μ)加上学习的标准偏差(σ)乘以epsilon(ε),其中ε遵循正态分布。 我们重新参数化样本,使随机性与参数无关。
def reparameterize(self, mu: Variable, logvar: Variable) -> Variable:
#mu : mean matrix
#logvar : variance matrix
if self.training:
std = logvar.mul(0.5).exp_() # type: Variable
eps = Variable(std.data.new(std.size()).normal_())
return eps.mul(std).add_(mu)
else:
return mu
在我们的示例中,我们将尝试使用变分自动编码器生成新图像。 我们将使用MNIST数据集,重建的图像将是手写的数字。 正如我已经告诉过你的那样,除了熟悉之外,我使用Pytorch作为框架,没有特别的原因。 首先,我们应该定义我们的图层。
def __init__(self):
super(VAE, self).__init__()
# ENCODER
self.fc1 = nn.Linear(784, 400)
self.relu = nn.ReLU()
self.fc21 = nn.Linear(400, 20) # mu layer
self.fc22 = nn.Linear(400, 20) # logvariance layer
# DECODER
self.fc3 = nn.Linear(20, 400)
self.fc4 = nn.Linear(400, 784)
self.sigmoid = nn.Sigmoid()
如您所见,我们将使用一个非常简单的网络,只有Dense(在pytorch的情况下为Linear)层。 下一步是构建运行编码器和解码器的功能。
def encode(self, x: Variable) -> (Variable, Variable):
h1 = self.relu(self.fc1(x))
return self.fc21(h1), self.fc22(h1)
def decode(self, z: Variable) -> Variable:
h3 = self.relu(self.fc3(z))
return self.sigmoid(self.fc4(h3))
def forward(self, x: Variable) -> (Variable, Variable, Variable):
mu, logvar = self.encode(x.view(-1, 784))
z = self.reparameterize(mu, logvar)
return self.decode(z), mu, logvar
它只是几行python代码。 没什么大不了。 最后,我们将训练我们的模型并查看生成的图像。
快速提醒:与tensorflow相比,Pytorch有一个动态图表,这意味着代码在运行中运行。 没有必要创建图形然后编译执行它,Tensorflow最近以其急切的执行模式引入了上述功能。
optimizer = optim.Adam(model.parameters(), lr=1e-3)
def train(epoch):
model.train()
train_loss = 0
for batch_idx, (data, _) in enumerate(train_loader):
data = Variable(data)
optimizer.zero_grad()
recon_batch, mu, logvar = model(data)
loss = loss_function(recon_batch, data, mu, logvar)
loss.backward()
train_loss += loss.data[0]
optimizer.step()
def test(epoch):
model.eval()
test_loss = 0
for i, (data, _) in enumerate(test_loader):
data = Variable(data, volatile=True)
recon_batch, mu, logvar = model(data)
test_loss += loss_function(recon_batch, data, mu, logvar).data[0]
for epoch in range(1, EPOCHS + 1):
train(epoch)
test(epoch)
培训完成后,我们执行测试功能以检查模型的工作情况。 事实上,它做得非常好,构造的图像与原始图像完全相同,我相信没有人能够在不知道整个故事的情况下将它们区分开来。
下图显示了第一行中的原始照片和第二行中的原始照片。
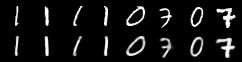
相当不错,不是吗?
在我们结束这篇文章之前,我想再介绍一个主题。 如我们所见,变分自动编码器能够生成新图像。 这是生成模型的经典行为。 生成模型正在生成新数据。 另一方面,判别模型是对类或类别中的现有数据进行分类或区分。
用一些数学术语来解释:生成模型学习联合概率分布p(x,y),而判别模型学习条件概率分布p(y | x)。
在我看来,生成模型更有趣,因为它们为从数据增加到模拟未来可能状态的众多可能性打开了大门。 但更多关于下一篇文章的内容。 关于一种称为生成性对抗性网络的相对较新的生成模型的帖子。
在那之前,继续学习AI。