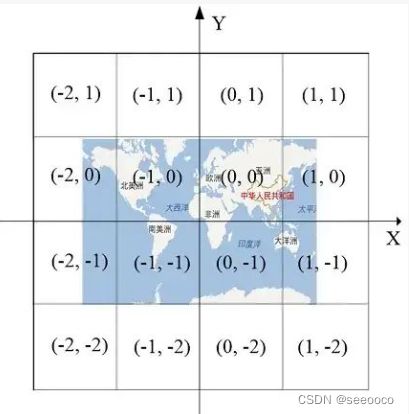
地图学数学基础
1.地球的数学模拟
[1]大地水准面Geoids
假设当海水处于完全静止的平衡状态时,从海平面延伸到所有大陆下部, 而与地球重力方向处处正交的一个连续、闭合的曲面,这就是大地水准面,但是大地体并不能使用相应的数学表示。
大地测量中用水准量测方法得到地面上各点的高程就是依据这个水准面来确定的,大地水准面上任何一点的铅垂线都与大地水准面成正交,而铅垂线的方向又受地球内部质量分布不均匀和地面高低起伏的影响,致使大地水准面产生微小起伏,所以大地水准面仍是一个不规则的、不能用简单数学公式表达的曲面。
大地水准面不同于平均海平面。
[2]旋转椭球体rotational ellipsoid
在数学上的定义:椭圆围绕其短轴或长轴旋转而成的球体
在地球上的定义:旋转椭球体是大地体经绕地轴(短轴)旋转而成的表面光滑的球体,既与地球的真实形状十分相似,也可以使用简单的数学公式表达称为地球椭球体,其表面称为地球椭球面,地球椭球面的方程为:
x 2 a 2 + y 2 a 2 + z 2 b 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{a^2}+\frac{z^2}{b^2}=1 a2x2+a2y2+b2z2=1
所有经线圈都是相等的椭圆,而赤道和所有纬线圈都是正圆。
表征地球椭球体的主要参数有椭球长半径 a a a、短半径 b b b、扁率 α \alpha α、第一偏心率 e e e、第二偏心率 e ’ e’ e’
a = a − b a e 2 = a 2 − b 2 a 2 e ′ 2 = a 2 − b 2 b 2 a=\frac{a-b}{a}\\ e^2=\frac{a^2-b^2}{a^2}\\ e'^2=\frac{a^2-b^2}{b^2} a=aa−be2=a2a2−b2e′2=b2a2−b2
[3]参考椭球体reference ellipsoid
参考椭球体——拥有特定地球椭球体参数的定义的椭球体
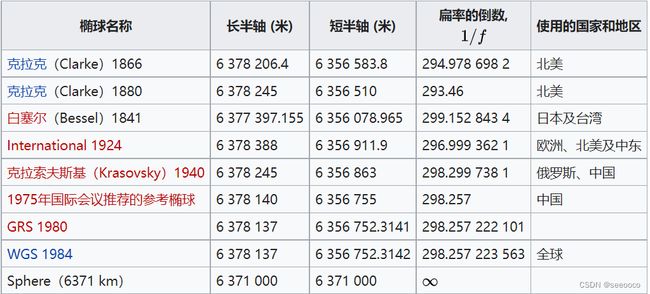
由于推算的年代、测量技术、与方法及其测定地区的不同,地球椭球体的参数并不一致。下面为常见的参考椭球体地球椭球体及其参数
- 1940年北京坐标系:克拉索夫斯基(Krasovsky)椭球体
- 西安80:1975
- 国家2000:CGCS2000椭球
[4]大地基准面Datum
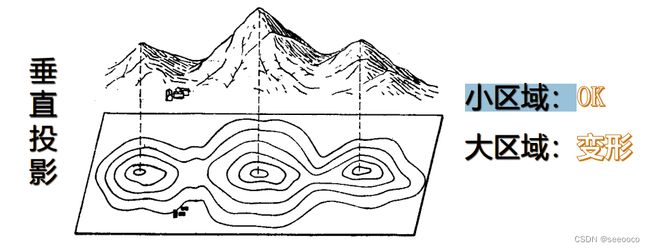
有了参考椭球,在实际建立地理空间坐标系统的时候,还需要指定一个大地基准面将这个椭球体与大地体联系起来。
讲白了,就是地球椭球体只是近似的代表地球,为了尽量减少针对各个地区的近似误差,即通过大地基准面使得地球椭球体与地球体在某一区域尽量重合。因此,各个地区为了使得地球椭球体与地球体尽量重合,导致有很多不同的大地基准面,如北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。下图可解释大地基准面的作用。
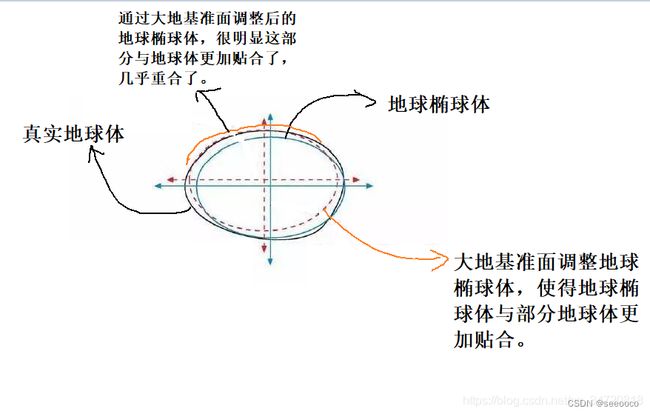
那么为了使得地球椭球体通过平移、旋转、缩放与地球体更加贴合,大地基准面就需要7参数分别为:三个平移参数 Δ X 、 Δ Y 、 Δ Z ΔX、ΔY、ΔZ ΔX、ΔY、ΔZ;三个旋转参数 ε x 、 ε y 、 ε z εx、εy、εz εx、εy、εz;最后是比例校正因子,用于调整椭球大小。
- 地心基准面:由卫星数据得到,使用地球的质心作为原点, WGS 1984,CGCS200坐标系
- 区域基准面:特定区域内与地球表面吻合,大地原点是参考椭球与大地水准面相切的点,例如
Beijing54、Xian80。 我们通常称谓的Beijing54、Xian80坐标系实际上指的是我国的两个大地基准面
我们通常说的参心大地坐标系和地心大地坐标系的区别就在于此。
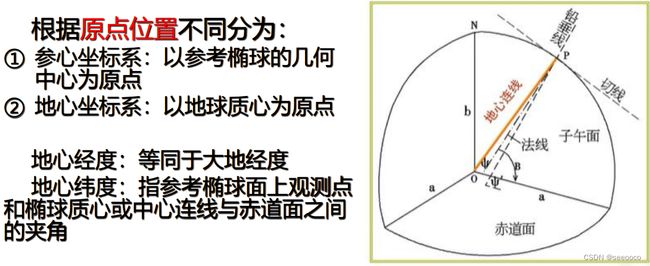
参心大地坐标系(区域基准面):指经过定位与定向后,地球椭球的中心不与地球质心重合而是接近地球质心。区域性大地坐标系。是我国基本测图和常规大地测量的基础。如Beijing54、Xian80。
地心大地坐标系(地心基准面):指经过定位与定向后,地球椭球的中心与地球质心重合。如CGCS2000、WGS84
2.地理坐标系GCS
Geographical Coordinate System指用经度和纬度表示地面点位的球面坐标
[1]地理坐标系分类
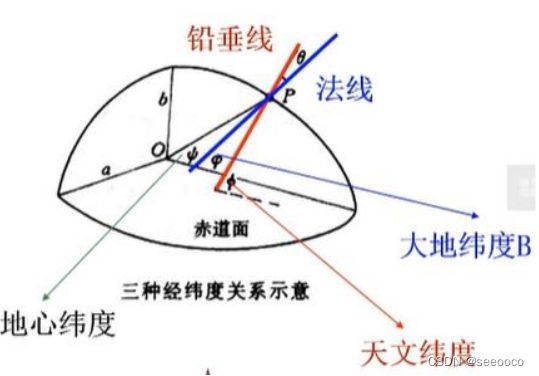
一般地理坐标可分为三种,天文经纬度,大地经纬度,地心经纬度。通常地图上使用的经纬度都为大地经纬度
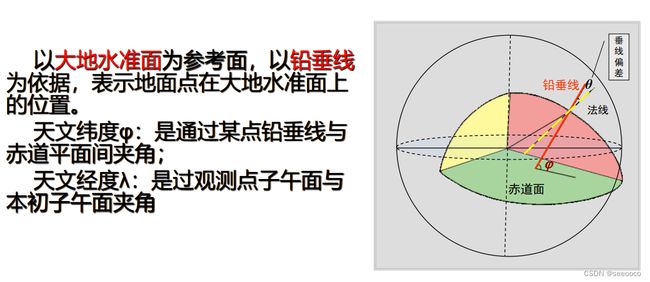
天文经纬度
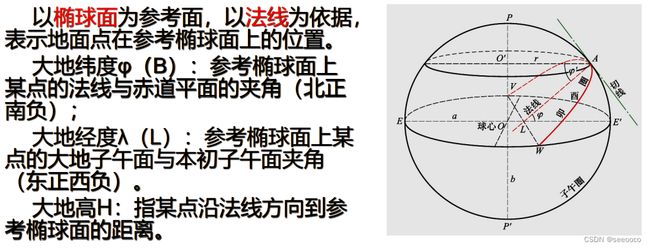
大地经纬度
地心经纬度
在大地测量学中,常用天文经纬度定义地理坐标。 在地图学中,以大地经纬度定义地理坐标。 在地理学研究以及地图学小比例尺 制图中,通常将椭球体当成正球体看, 采用地心经纬度 。
[2]常见的地理/大地坐标系
地理/大地坐标系是大地测量中以参考椭球面为基础建立起来的(基准面)坐标系。地面点的位置用大地经度、大地纬度和大地高度表示
参心坐标系
-
1954北京坐标系
-
1980国家大地坐标系
地心坐标系
- 2000国家大地坐标系(注意区分CGCS2000椭球体)
- WGS84坐标系(注意区分WGS84椭球体)
地理/大地坐标系=椭球体+基准面组成
3.高程系统
高程系统是指相对于不同性质的起算面(大地水准面,似大地水准面、椭球面等)所定义的高程体系
[1]高程系统分类
高程系统的基准面基本上有两种:一是大地水准面,它是正高和力高的基准面;二是参考椭球表面,它是大地高程的基准面。此外,为了克服正高不能精确计算的困难还采用正常高,以似大地水准面为基准面,它非常接近大地水准面。
- 大地水准面—>**正高系统:**地球上一点到大地水准面的距离。平均重力无法精确测得,所以正高无法精确得到
- 似大地水准面—>**正常高系统:**地球上一点到似大地水准面的距离。沿重力线方向可以精确测得的
- 参考椭球体—>**大地高系统:**沿法线方向到参考椭球的距离,大地高一般用符号H表示,常见的地理坐标(B,L,H)便是采用此高程系统
大地高=正常高系统+高程异常
大地高=正高系统+大地水准面差距
我国高程采用的是正常高和大地高系统。通常用到的地理坐标系高程都是大地高,通常外业用水准测得的是正常高。
[2]转换
不同椭球大地高的转换
三维七参数模型进行转换
不同高程基准正常高转换
我国目前采用的高程基准是1985国家高程基准,但是还有其他高程基准,例如1954黄海高程基准。这种情况就要获得不同高程基准间的改正数。
大地高和正常高的转换
(1)如果是北京54或西安80这种参心坐标系。获得高程异常后,按大地高和正常高之间关系公式直接计算。
(2)WGS84/CGCS2000大地高与1985国家高程基准间的转换
[3]我国常用的高程基准面
-
1956黄海高程系统
-
1985国家高程基准
4.投影
[1]简介
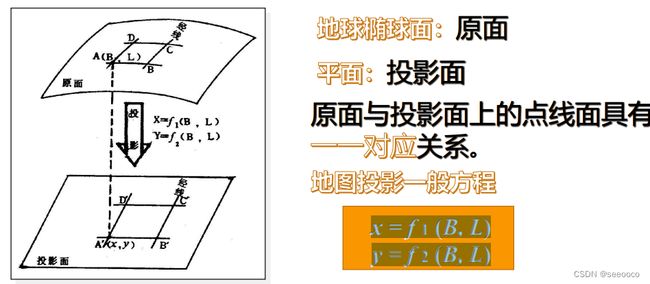
在地球椭球面和平面之间建立点与点之间函数关系的数学方法,称为地图投影。(比如是将地球展开画到平面上)
投影坐标系:为平面坐标。参考平面地是水平面,坐标单位:米、千米等;
投影坐标系的生成是以地理坐标系为基准的,所以每个投影坐标系前面都会挂有地理坐标系
而地理坐标系后面的一串,则是投影参数。 比如 Beijing 1954/3-degree Gauss-Kruger zone 39,意思是:3度分带法的北京54坐标系,中央经线在东117度的分带坐标,横坐标前加带号
[2]投影方法
几何透视法
数学分析法
[3]投影方式分类
地球椭球表面是一种不可能展开的曲面,要把这样一个曲面表现到平面上,就会发生裂隙或褶皱。 在投影面上,可运用经纬线的“拉伸”或“压缩”(通过数学手段)来加以避免,以便形成一幅完整的地图。但不可避免会产生变形。 地图投影的变形通常有:长度变形、面积变形和角度变形。在实际应用中,根据使用地图的目的,限定某种变形。
根据不同的需要,我们会选择不同的投影组合
按变形性质分类
等角投影
- 角度变形为零(
Mercator)[条件:w=0,a=b] - 我国大中比例尺地形图上所采用的
高斯—克吕格投影就是等角横切椭圆柱投影。 小比例尺地形图和航空图则采用等角圆锥投影 - 墨卡托:正轴等角圆柱投影
等面积投影
- 面积变形为零(
Albers)[条件:p=a*b=1]
任意投影
-
长度、角度和面积都存在变形(其中,各种变形相互联系相互影响,等积与等角互斥,等积投影角度变形大,等角投影面积变形大)[条件:
a=1或b=1] -
等距离投影是任意投影中的一个
补充:
- 标准纬线
在地图投影中不变形的纬线。投影平面切在某点,该点在球面上,也在投影平面上这样的点投影后不产生任何变形。 圆锥与地球某纬线圈相切,圆柱在赤道上与地球相切,这些相切的纬线投影后均无变形
- 等变形线
等变形线是投影变形值相等点的连线,有面积和角度等变形线之分。等变形线与没有变形的点和线,组成了变形分布的系统。 在投影略图上绘出等变形线,用来表示变形分布的情况及其投 影使用的优劣。等变形线的形状在一些投影中是规则的,如与纬 线形状一致或以投影中心为圆心的圆等,但大多数是不规则的曲线。
从投影面类型划分
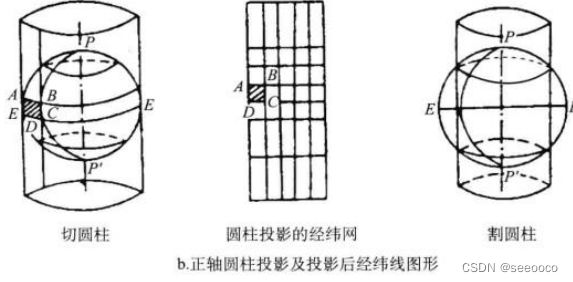
圆柱投影
以圆柱面为投影面,将经纬网投影到圆 柱面上,然后将圆柱面展成平面
根据圆柱面和地球面的相对位置,圆柱投影分为正圆柱、横圆柱和斜圆柱
根据圆柱面和地球面的相互关系不同,可分为切圆柱投影和割圆柱投影
圆锥投影
以圆锥面为投影面,将圆锥与地球相割或相切,将经纬网投影到圆锥面上,然后将圆锥面展成平面
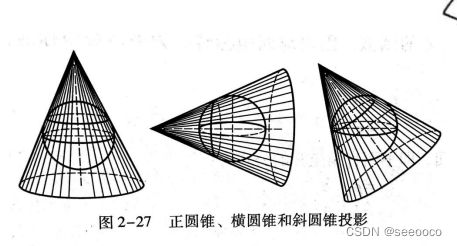
根据圆锥面和地球面的相对位置,圆锥投影分为正圆锥、横圆锥和斜圆锥
根据圆锥面和地球面的相互关系不同,可分为切圆锥投影和割圆锥投影
方位投影
投影面为平面,平面与地球面构成相割或相切的位置关系,将经纬网投影到平面上,根据投影面和地球面的相对位置,方位投影分为正方位(切点在两级)、横方位(切点在赤道)和斜方位(切点在赤道和两级之间)几种投影
从投影面与地球位置关系划分为
正轴投影:投影面中心轴与地轴相互重合
斜轴投影:投影面中心轴与地轴斜向相交
横轴投影:投影面中心轴与地轴相互垂直
相切投影:投影面与椭球体相切
相割投影:投影面与椭球体相割
[4]投影坐标系
投影坐标系=地理坐标系+投影方法
[5]我国常用的投影
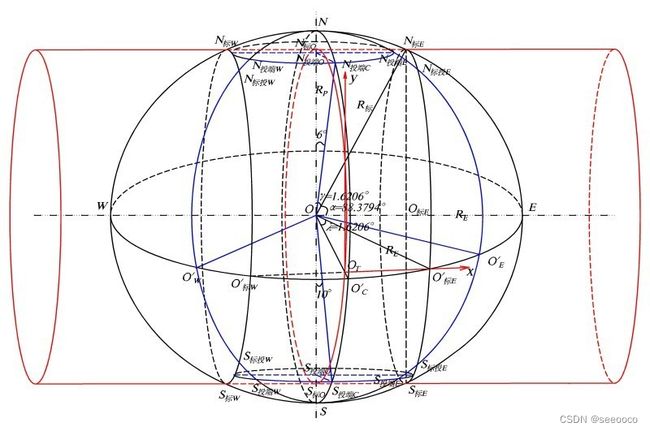
我国基本比例尺地形图(1:100万、1:50万、1:25万、1:10万、1:5万、1:2.5万、1:1万、1:5000) **除1:100万以外均采用高斯-克吕格Gauss-Kruger投影(**横轴等角切圆柱投影,又叫横轴墨卡托Transverse Mercator投影)为地理基础。 1:100万地形图采用兰伯特Lambert投影(正轴等角割圆锥投影),其分幅原则与国际地理学会规定的全球统一使用的国际百万分之一地图投影保持一致。 海上小于50万的地形图多用墨卡托Mercator投影(正轴等角圆柱投影)。 我国大部份省区图以及大多数这一比例尺的地图也多采用Lambert投影和属于同一投影系统的Albers投影(正轴等积割圆锥投影)。
高斯-克吕格Gauss-Kruger投影(横轴等角切圆柱投影)
高斯—克吕格投影亦称为横轴 墨卡托投影,简称TM 投影
我国规定1:1万、1:2.5万、1:5万、1:10万、1:25万、1:50万比例尺的地形图均采用高斯克吕格投影。该投影在英美等国家被称为横轴墨卡托投影
特点
- 离中央经线越远的地区,面积变化越大。
- 此投影合适用于导航
- 投影椭圆柱面是横着的
- 投影椭圆柱面与椭球体相切
兰伯特Lambert投影(正轴等角割圆锥投影)
墨卡托Mercator投影(正轴等角圆柱投影)
地球面上一条与所有经线相交成等方位角的曲线称为等角航线
等角航线被投影为直线,便于航迹绘算。 等角性质投影,保持图上方位与实地一致。 经纬线形状简单,便于绘制
特点:
- 没有角度变形,图上方位与实地保持一致;
- 标准纬线上没有变形;
- 两极变形趋向无穷大
通用墨卡托投影UTM
通用横墨卡托投影,简称UTM投影,几何上理解为横轴等角割圆柱投影,标记南纬80°至北纬84°之间的所有位置。
UTM投影与高斯—克吕格投影之间没有实质性 的差别,其投影条件与高斯—克吕格投影相比,除 中央经线长度比m0为0.9996以外,其他条件相同。 UTM投影改善了高斯—克吕格投影在低纬度地 区的变形。世界上许多国家的地形图采用UTM投影作数学基础
UTM投影分带
UTM 经度区范围为1到60,其中58个区的东西跨度为 6°。经度区涵盖了地球中纬度范围从 80°S 到 84°N 之间的所有区域。一共有 20个UTM 纬度区,每个区的南北跨度为 8°;使用字母 C 到 X 标识(其中没有字母 I 和 O)。A、B、Y、Z 区不在系统范围以内,它们覆盖了南极和北极区。
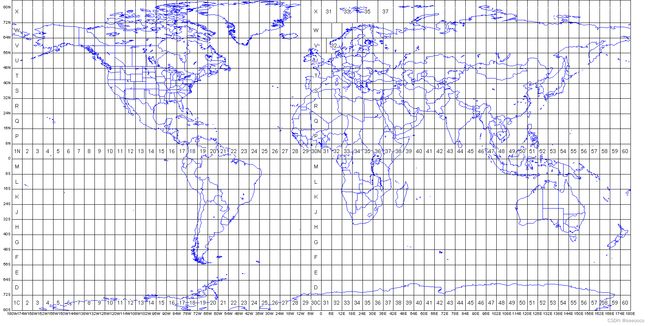
UTM投影与高斯-克吕格投影的区别
(1) 中央经线长度比不同,UTM投影是0.9996,而高 斯-克吕格投影是1。
(2)带的划分相同,而带号的起算不同。带号相差30。
(3)对于中、低纬度地区,UTM投影的变形优于高斯克吕格投影。
(4)西方国家(美、英、德、法)多采用UTM投影作为 国家基本地形图投影,东方国家(中、苏、蒙、朝)多采 用高斯-克吕格投影作为国家基本地形图投影
6.坐标参考系统(Coordinate Reference Systems CRS)
GIS中的坐标参考系统(Coordinate Reference Systems CRS)分为两大类:投影坐标系PCS和地理坐标系GCS
一个投影坐标系统,必然包括一个投影方法和一个地理坐标系统的定义
注意:空间参考系spatial reference system(SRS不等于坐标参考系CRSCoordinate Reference Systems),空间参考系SRS包含坐标参考系CRS,坐标参考系是空间参考系的必要组成部分。
可以联想postgis中空间参考系表spatial_ref_sys中包含的内容
[1]WKID与EPSG
WKID即Well Known ID,众所周知的ID号的意思。EPSG是管理这些ID号的一个组织,网站是epsg.io
一个GIS里的坐标系统,必须有一个WKID(地理坐标系统和投影坐标系统均可使用WKID定义,尽管投影坐标系=地理坐标系统+投影,其地理坐标系统的WKID和投影坐标系统的WKID是无关联的)
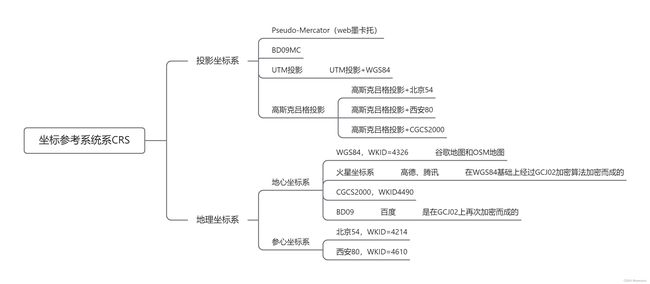
[2]常见地理坐标系统GCS
见上图
[3]常见投影坐标系统PCS
基于于高斯克吕格投影的投影坐标系统
在我国北京54、西安80、国家2000地理坐标系统,均可以使用高斯克吕格投影定义出投影坐标系统
同一个地理坐标系统通常有多个投影投影坐标系统(其WKID也是不同的),可以根据需求选择,下面为一些示例
在ArcGIS中,不同的GCS(地理坐标系)的PCS(投影坐标系)是不同的,以CGCS2000、西安80和北京54为例:
CGCS2000_3_Degree_GK_CM_111E:CGCS2000的GCS下,使用高斯克吕格3度分带法,以中央经线为东经111度的投影带的投影坐标系(WKID: 4546 )
CGCS2000_3_Degree_GK_Zone_30:CGCS2000的GCS下,使用高斯克吕格3度分带法,第30个投影带的投影坐标系(WKID: 4518 )
Beijing_1954_3_Degree_GK_CM_111E:北京54的GCS下,使用高斯克吕格3度分带法,以中央经线为东经111度的投影带的投影坐标系(WKID: 2434)
Beijing_1954_3_Degree_GK_Zone_35:北京54的GCS下,使用高斯克吕格3度分带法,第35个投影带的投影坐标系(WKID: 2401 )
Xian_1980_3_Degree_GK_CM_111E:西安80的GCS下,使用高斯克吕格3度分带法,以中央经线为东经111度的投影带的投影坐标系(WKID: 2382)
Xian_1980_3_Degree_GK_Zone_34:西安80的GCS下,使用高斯克吕格3度分带法,第34个投影带的投影坐标系(WKID: 2358)
- 名称中有CM,在Y坐标(经线方向)不带带号
- 名称中有Zone,则在Y坐标(经线方向)带带号
基于UTM投影的投影坐标系统
类似于高斯克吕格投影坐标系统,只不过通常的组合是UTM投影+WGS84地理坐标系统,其组合与分代规同上。
基于网络墨卡托(WebMercator)投影的投影坐标系统
只有一个,WebMercator投影+WGS84地理坐标系 WKID=3857
[4]各大地图厂商使用的坐标系
- 谷歌地图和OSM地图——>
WGS84坐标系 - 天地图——>
CGCS2000坐标系 - 高德、腾讯——>
GCJ02坐标系,GCJ02坐标系是在WGS84基础上加密而成的。 - 百度——>
BD09坐标系,是在GCJ02上再次加密而成的。
- WGS84\CGCS2000是原始坐标系,GCJ02\BD09是加密坐标系。
- UTM投影坐标系经常应用在无人驾驶及高精地图上面;
- 国内Android系统手机采集的AGPS数据是GCJ02坐标系的;
- RTK和一些PDA设备采集的GPS数据是WGS84坐标系的;
- IOS系统手机采集的AGPS数据是WGS84坐标系的;
- GPS定位芯片获取的定位数据是WGS84坐标系的;
- 北斗芯片获取的定位数据是CGCS2000坐标系的。
大多数情况下,我们可以认为CGCS2000坐标系=WGS84坐标系,很多软件和框架都还没有兼容CGCS2000坐标系,我们在使用CGCS2000坐标系的数据的时候,可以设置为WGS84坐标系,这样也便于传输和查阅。
7.数据中坐标参考系统
[1]判别
- 如果数据的元数据坐标系统的定义,则可以从数据的元数据中得知坐标系
- 如果数据的元数据没有坐标系统定义,需要通过观察数据坐标值来判断GCS、PCS类型,则需要一定的经验。
- 如果数据是两位数+三位数或者三位数+三位数等落于我国经纬度范围的数字,则可以大致判断是地理坐标系统,只需询问数据提供者,然后自己为数据定义地理坐标系统即可。
- 如果给的数据尺度很小,例如是一个厂房,而且一个单位数值差不多就是1米,则判断是CAD绘图,是未经校准的平面直角坐标系,可以理解为投影坐标系,只不过位置并不准确罢了,需要校准。
- 如果给的数据单位很大,通常是几万、几十万(5位数+6位数,是无投影带的,5位数是经线x方向,6位数是纬线y方向)(6位数+7位数,是有投影带的,6位数是纬线y方向,7位数是经线x方向,通过7位数的前两个数字判断投影带),此时可以粗略判断是投影坐标系统。
- 如果均不是以上的数值,则判断为误操作,可能是错误定义了坐标系,也可能是错误进行投影计算。
[2]定义投影
在arcgis - arcmap中,在数据管理工具箱>投影工具集下,是处理坐标系统的强大工具。
- “定义投影”工具,是为无坐标系统定义的数据定义GCS或PCS用的;
[3]转换投影
- 数据管理工具箱->投影工具集->“投影”工具,是转换坐标系统用的,可以由GCS投影到指定PCS,也可以由PCS转到指定GCS(可以是PCS定义内的GCS,也可以是其他GCS),也可以由PCS转到另一个PCS(换投影带,或者连GCS、PCS一起换)
8.瓦片坐标系
- 谷歌地图、OSM、高德、腾讯、等都使用谷歌的瓦片地图规范
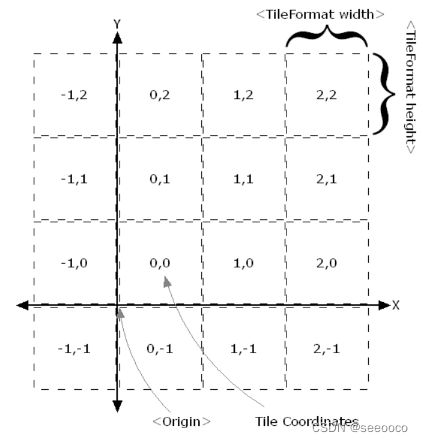
- Z表示缩放层级,从0开始;
XY的原点在左上角,X从左向右,Y从上向下
[2]WMTS规范
- 切片原点为左下角,X 轴向右,Y 轴向上
- 腾讯地图采用
- WMTS瓦片可为矩形或正方形
[3]TMS规范
- 切片原点为左下角
- TMS瓦片固定了为正方形
[4]百度地图
- Z从1开始,在最高级就把地图分为四块瓦片;XY的原点在经纬度位0的位置,X从左向右,Y从下向上
[5]bing地图
QuadTree:微软Bing地图使用的编码规范,Z的定义与谷歌相同,同一层级的瓦片不用XY两个维度表示,而只用一个整数表示,该整数服从四叉树编码规则
9.坐标参考系统的表达
常见的坐标参考系的表达有的WKT、Proj4表达、EPSG的WKID方式
proj.4表达式
+proj=longlat +datum=WGS84 +no_defs
EPSG表达式
EPSG:4326
WKID=4326的WKT表达
GEOGCS["WGS 84", //GEOGCS定义地理坐标系统,第一个属性"WGS 84"为该坐标系的名字
DATUM["WGS_1984",//基准面"DATUM"
SPHEROID["WGS 84",6378137,298.257223563,//"SPHEROID"是椭球体名称和长半轴长和扁率的倒数
AUTHORITY["EPSG","7030"]],
AUTHORITY["EPSG","6326"]],
PRIMEM["Greenwich",0,//中央经线Greenwich,0度标准子午线
AUTHORITY["EPSG","8901"]],
UNIT["degree",0.0174532925199433,//转换因子0.0174532925199433
AUTHORITY["EPSG","9122"]],
AUTHORITY["EPSG","4326"]]
WKT(Well-known text),是一种文本标记语言,用于表示矢量几何对象、空间参照系统及空间参照系统之间的转换。
10.不同坐标参考系统的转换
一个坐标系统挪到另一个坐标系统,有哪些情况呢?
坐标系统转换的通常就是地理坐标系统之间的转换,也即椭球体的之间转换。直接转换投影坐标系是比较复杂的
[1]三参数转换
平移原点,只需要给出三个方向的平移量 d x 、 d y 、 d z dx、dy、dz dx、dy、dz
[2]七参数转换
三个平移参数 d x 、 d y 、 d z dx、dy、dz dx、dy、dz + 三个方向的旋转角度 α 、 β 、 γ α、β、γ α、β、γ + 统一的缩放比例 k k k
[3]四参数转换
也就是只在二维平面的情况,通过控制两个平移量 d x 、 d y dx、dy dx、dy,一个旋转角度 α α α,一个缩放比例 k k k参数
11.地图投影前端实现与转换
turf.js
proj
。。。