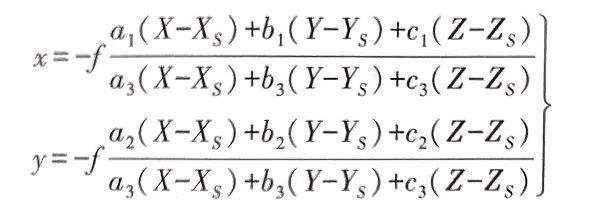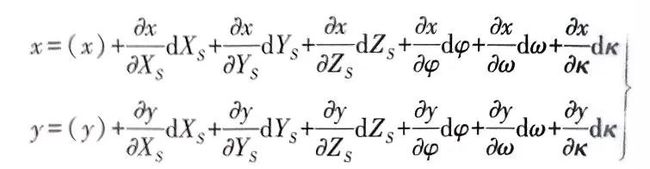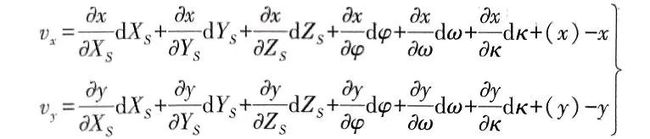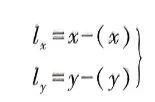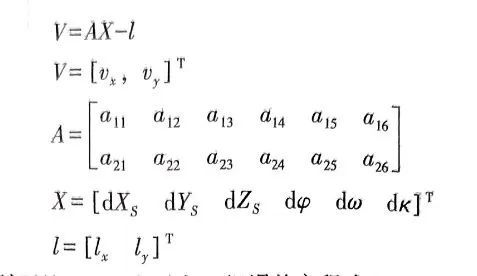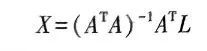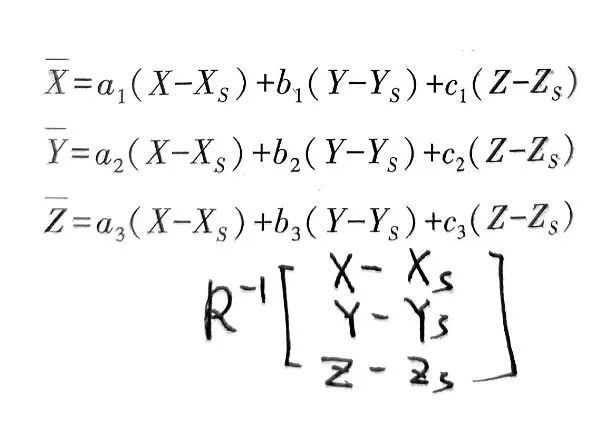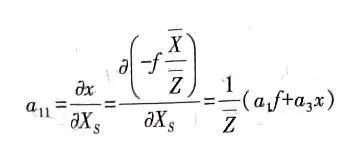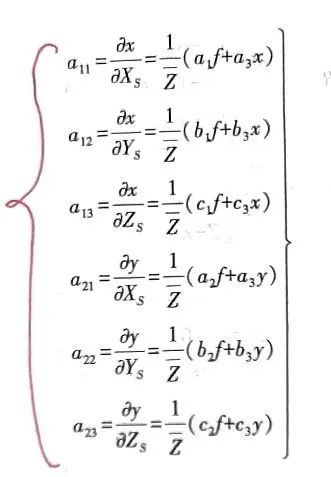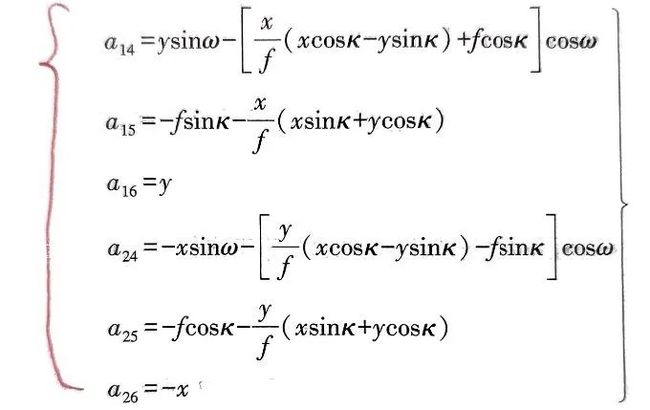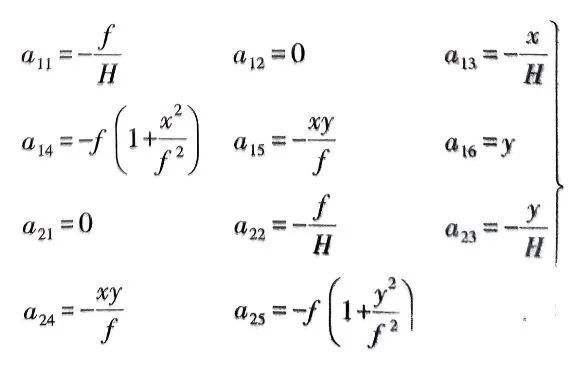单像空间后方交会的程序实现

单像空间后方交会概述

如果已知每张像片的6个外方位元素，就能确定被摄物体与航摄像片的关系，因此如何获取像片的外方位元素是摄影测量工作者所探讨的问题。

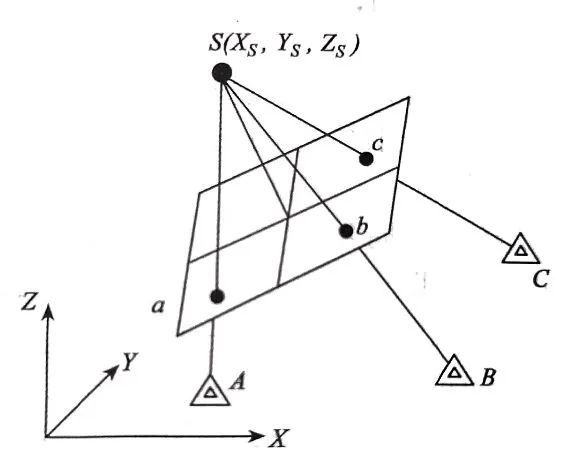
摄影测量空间后方交会就是利用至少三个已知地面控制点的坐标 A、B、C (X, Y, Z) 与其影像上对应的三个像点的影像坐标 a, b, c (x,y)，根据共线方程，反求该相片外方位元素的方法。

单像空间后方交会

单像空间后方交会的算法原理

我们利用共线方程，假定像点的影像坐标为观测值，地面控制点的三维坐标为真值进行间接平差。

共线方程

 我们可以发现共线方程是非线性的函数模型，为便于计算我们首先利用泰勒公式展开成线性形式。

共线方程的线性化形式
我们可以发现共线方程是非线性的函数模型，为便于计算我们首先利用泰勒公式展开成线性形式。 

 

其中(x)与(y)为像点影像坐标的近似值，我们可以在假定外方位元素计算初始值后经行计算。

在竖直摄影的情况下角元素初始值均为0，而各线元素的数值为控制点的平均值。

其中(x)与(y)为像点影像坐标的近似值，我们可以在假定外方位元素计算初始值后经行计算。

在竖直摄影的情况下角元素初始值均为0，而各线元素的数值为控制点的平均值。

在经行间接平差时我们可以将线性方程移项构成

“观测值改正数 = 真值近似值 + 观测值近似值 - 观测值”

 

 我们通常用矩阵形式表示

 

 根据最小二乘原理未知数的向量解可算出。

 

 为方便求导我们把共线方程拆开并记作:

 

 小秦的字迹是去不掉惹(笑)

 

同理我们就可以计算出其他系数阵的数值函数关系。 

 

 线元素的系数

 

 角元素系数

 当然竖直摄影情况下可以直接用各系数近似值计算：

 

 

 单像空间后方交会的程序实现

# 像点类，实例化像点需要像点的各计算数据以完整像点的像平面坐标、空间辅助系坐标、地面摄影测量坐标系坐标
class PicturePoint():
    # 初始化参数:主距f、控制点字典CC_dict(Control Point Coordinate)、像点影像坐标字典(Image Coordinate)、外方位元素字典
    def __init__(self,f,ControlCoordinate_dict,ImageCoordinate_dict,LineElement_dict = {},AngleElement_dict = {'fi':0,'omiga':0,'kapa':0},vertical=0):
        # 输入的参数
        self.f = f
        self.ControlCoordinate_dict = ControlCoordinate_dict
        self.ImageCoordinate_dict = ImageCoordinate_dict
        self.LineElement_dict = LineElement_dict
        self.AngleElement_dict = AngleElement_dict
        
        # 旋转矩阵的计算
        self.fi = h2d(AngleElement_dict['fi'])
        self.omiga = h2d(AngleElement_dict['omiga'])
        self.kapa = h2d(AngleElement_dict['kapa'])
        self.fi_h = d2h(self.fi)
        self.omiga_h = d2h(self.omiga)
        self.kapa_h = d2h(self.kapa)
        self.vertical = bool(vertical)
        self.ControlCoordinate_df = pd.DataFrame(ControlCoordinate_dict)
        self.ImageCoordinate_df = pd.DataFrame(ImageCoordinate_dict)

 类名为PicturePoint，因为个人认为我们整个程序操作的对象为像点，其初始化的数值为主距f，控制点字典ControlCoordinate_dict，像点影像坐标字典ImageCoordinate_dict，外方位元素AngleElement_dict = {'fi':0,'omiga':0,'kapa':0}初始值设为0；ControlCoordinate_df 、ImageCoordinate_df 为pandas的DataFrame结构方便数据查询。

# φωκ各自的的旋转阵
        self.R_fi = np.array([[math.cos(self.fi_h),0,-math.sin(self.fi_h)],
                              [0,1,0],
                              [math.sin(self.fi_h),0,math.cos(self.fi_h)]])
        self.R_omiga = np.array([[1,0,0],
                                 [0,math.cos(self.omiga_h),-math.sin(self.omiga_h)],
                                 [0,math.sin(self.omiga_h),math.cos(self.omiga_h)]])
        self.R_kapa = np.array([[math.cos(self.kapa_h),-math.sin(self.kapa_h),0],
                              [math.sin(self.kapa_h),math.cos(self.kapa_h),0],
                              [0,0,1]])
        # 总旋转矩阵
        self.R = [email protected][email protected]_kapa
        self.R_inv = inv(self.R)

 而后为旋转矩阵的定义

# 取各点的控制点坐标平均值为像点坐标的初始值
        if LineElement_dict == {}:
            self.Xs0 = np.average(self.ControlCoordinate_df['X'])
            self.Ys0 = np.average(self.ControlCoordinate_df['Y'])
            self.Zs0 = np.average(self.ControlCoordinate_df['Z'])
            self.LineElement0_list = np.array([self.Xs0,self.Ys0,self.Zs0])
            self.LineElement_dict = {'Xs':self.Xs0,'Ys':self.Ys0,'Zs':self.Zs0}
        else:
            self.LineElement_dict = LineElement_dict
            self.LineElement0_list = LineElement_dict
            self.Xs0 = LineElement_dict['Xs']
            self.Ys0 = LineElement_dict['Ys']
            self.Zs0 = LineElement_dict['Zs']
            self.LineElement0_list = np.array([self.Xs0,self.Ys0,self.Zs0])

 

计算线元素初始值

if-else用于辨别类实例化时是否输入线元素，若线元素为空{}，则在类中自动初始化计算线元素为控制点均值，以方便迭代。

# 系数阵计算
        A = np.array([])
        l = np.array([])
        self.x0y0 = {'x0':[],'y0':[]}
        self.L = np.array([])
        for i in range(len(self.ControlCoordinate_df)):
            # C_I为控制点坐标减线方位元素初始值
            C_I = np.array([self.ControlCoordinate_df.loc[i]]) - self.LineElement0_list
            C_I = C_I.T
            # X_,Y_,Z_分别为共线方程分子分母，详情见书
            X_= self.R[0]@C_I
            Y_= self.R[1]@C_I
            Z_= self.R[2]@C_I
            x = self.ImageCoordinate_dict['x'][i]
            y = self.ImageCoordinate_dict['y'][i]
            f = self.f
            # 像点坐标近似值x0,y0
            x0 = -f*(X_/Z_)
            y0 = -f*(Y_/Z_)
            # 系数计算
            a11 = (1/Z_)*(self.R[0,0]*f+self.R[2,0]*x)
            a21 = (1/Z_)*(self.R[1,0]*f+self.R[2,0]*y)
            a12 = (1/Z_)*(self.R[0,1]*f+self.R[2,1]*x)
            a22 = (1/Z_)*(self.R[1,1]*f+self.R[2,1]*y)
            a13 = (1/Z_)*(self.R[0,2]*f+self.R[2,2]*x)
            a23 = (1/Z_)*(self.R[1,2]*f+self.R[2,2]*y)
            omiga_h = self.omiga_h
            kapa_h = self.kapa_h
            a14 = y*math.sin(omiga_h) - ((x/f)*(x*math.cos(kapa_h) - y*math.sin(kapa_h))+f*math.cos(kapa_h))*math.cos(omiga_h)
            a15 = -f*math.sin(kapa_h)-(x/f)*(x*math.sin(kapa_h)+y*math.cos(kapa_h))
            a16 = y
            a24 = -x*math.sin(omiga_h) -((y/f)*(x*math.cos(kapa_h) - y*math.sin(kapa_h))-f*math.sin(kapa_h))*math.cos(omiga_h)
            a25 = -f*math.cos(kapa_h)-(y/f)*(x*math.sin(kapa_h)+y*math.cos(kapa_h))
            a26 = -x
            self.x0y0['x0'].append(float(x0))
            self.x0y0['y0'].append(float(y0))
            self.L = np.append(self.L,x)
            self.L = np.append(self.L,y)
            a_list = np.array([[float(a11),float(a12),float(a13),a14,a15,a16],[float(a21),float(a22),float(a23),a24,a25,a26]])
            l_list = np.array([[x-x0,y-y0]])
            l = np.append(l,l_list)
            A = np.append(A,a_list)

 

这里是系数阵的计算

这里使用了numpy简便地完成了矩阵的计算。

# 观测值向量
        self.L = self.L.reshape(len(self.L),1)
        # l向量
        self.l = l.reshape(len(l),1)
        # 系数阵A
        self.A = A.reshape(len(self.ControlCoordinate_df)*2,6)
        # 未知数向量（求解的方位元素）
        self.X = inv([email protected])@(self.A.T)@self.l
        # 新的角元素用于迭代
        self.new_AngleElement_dict = {'fi':float(self.X[3]),'omiga':float(self.X[4]),'kapa':float(self.X[5])}
        # 新的线元素
        self.new_LineElement_dict = {'Xs':float(self.X[0]),'Ys':float(self.X[1]),'Zs':float(self.X[2])}
        
        self.Xd = self.X[:3]
        for i in range(3,6) :
            angle = h2d(self.X[i])
            self.Xd = np.append(self.Xd,angle)
        # 协因数阵Q
        self.Q = inv((self.A.T)@self.A)
        # 改正数V
        self.V = [email protected] - self.l
        # 观测值改正后数值
        self.L_v = self.L + self.V
        # 新的像点坐标
        self.new_ImageCoordinate_dict = {'x':[],'y':[]}
        for i in range(int(len(self.L_v)/2)):
            self.new_ImageCoordinate_dict['x'].append(float(self.L_v[i]))
            self.new_ImageCoordinate_dict['y'].append(float(self.L_v[i+1]))
        # 中误差m0的平方m0_2
        self.m0_2 = np.sum(np.square(self.V))/(2*len(self.ControlCoordinate_df))

 

此处为间接平差模型的实现

注意：

new_ImageCoordinate_dict，

new_AngleElement_dict ，

new_LineElement_dict 

属性都可以用于直接作为迭代所用的参数直接引用。

对象的实例化操作

CCd = {'X':[36589.41,37631.08,39100.97,40426.54],'Y':[25273.32,31324.51,24934.98,30319.81],'Z':[2195.17,728.69,2386.50,757.31]}
ICd = {'x':[-86.15*10e-3,-53.40*10e-3,-14.78*10e-3,10.46*10e-3],'y':[-68.99*10e-3,82.21*10e-3,-76.63*10e-3,64.43*10e-3]}
P1 = PicturePoint(153.24*10e-3,CCd,ICd)

 注意单位统一，小秦一开始就忘了QwQ

P2 = PicturePoint(153.24*10e-3,CCd,P1.new_ImageCoordinate_dict,P1.new_LineElement_dict,P1.new_AngleElement_dict)

 当精度不合要求时可直接进行迭代，P2为P1的迭代新对象。

最后给大家分享一下小秦特供的角转换方法的程序哦，在小秦公众号原文里点原文链接就有了哦。

小秦最近有点点情绪波动，所有莫得怎么幽默了，Sorry捏！

我是普普通通有点憨憨的小秦，记得还要一起学习哦！