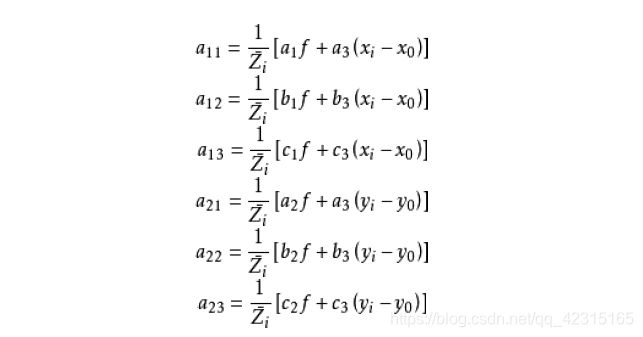单像空间后方交会（C语言）

---

1 原理介绍

1.1 定义

空间后方交会 (Space Resection)的定义：利用地面控制点(GCP,Ground Control Point)及其在像片上的像点，确定单幅影像外方位元素的方法。

如果我们知道每幅影像的6个外方位元素，就能确定被摄物体与航摄影像的关系。因此，如何获取影像的外方位元素，一直是摄影测量工作者所探讨的问题。可采取的方法有：利用雷达、全球定位系统（GPS）、惯性导航系统（INS）以及星相摄影机来获取影像的外方位元素；也可利用影像覆盖范围内一定数量的控制点的空间坐标与影像坐标，根据共线条件方程反求该影像的外方位元素，这种方法称为单幅影像的空间后方交会。

1.2 基本思想

以单幅影像为基础，从该影像所覆盖地面范围内的若干控制点的已知地面坐标和相应点的像坐标量测值出发，根据共线条件方程，运用最小二乘间接平差，求解该影像在航空摄影时刻的外方位元素。

由于共线方程是非线性函数，为了运用最小二乘法，必须先将其线性化。

共线条件方程的线性化

某一点的共线方程为：

式中，x,y 为这一点的像平面坐标，x0,y0,f 为影像的内方位元素， Xs,Ys,Zs 为摄站点的物方空间坐标， X,Y,Z 为这一点的物方空间坐标。 ai,bi,ci(i=1,2,3) 为影像旋转矩阵的九个元素，即：

因为未知数是外方位元素，所以将共线方程视为外方位元素的函数。设外方位元素的近似值为

将共线方程在外方位元素近似值处一阶泰勒展开，得：

式中 x0,y0 是把外方位元素近似值代入共线方程中得到的 x,y 。

列出误差方程

将控制点对应的像点的像平面坐标视为观测值，外方位元素视为参数，由共线方程的线性形式可列出误差方程：

式中 x,y 为控制点对应的像点的像平面坐标，Vx,Vy 为像平面坐标的改正数,

为参数的改正数。

以上两个方程为一个控制点列出。如果有 n 个控制点，则可以列出 2n 个方程。当 n>=3 时就可求解。

1.3 详细计算

获取已知数据

为了做空间后方交会，需要知道影像比例尺 1/m 、内方位元素 x0,y0,f 、控制点的空间坐标 X,Y,Z ，及其对应像点的像平面坐标 x,y。
影像比例尺可以从摄影资料中查取，也可以利用控制点的空间坐标和其对应像点的像平面坐标进行计算。

确定参数初值

参数的初值即
在竖直航空摄影且地面控制点大体对称分布的情况下，可按如下方法确定初值：

K0 可在航迹图上找出，或根据控制点坐标通过坐标正反变换求出。

计算旋转矩阵

利用角元素近似值计算方向余弦，组成旋转矩阵 R

下面列出三个矩阵相乘的结果供计算

计算像点坐标近似值

利用参数的近似值，按共线方程计算各个控制点对应像点的像平面坐标近似值

计算误差方程系数矩阵和常数项

一个控制点对应的误差方程为

写成矩阵形式为

其中

系数矩阵 A 中的元素均为偏导数。为了计算这些偏导数，引入以下记号：

由于推导过程较为复杂，此处省略，直接给出结果：

对每一个控制点，计算其对应的方程的系数矩阵 Ai 、常数项 Li ，然后联立起来，得：

记为

计算法方程系数矩阵和常数项

按最小二乘原理，取权阵为单位阵，则法方程为

这一步骤需要计算出 ATA 和 ATL 。

求解参数

按下式可求得 X 的值，即外方位元素的改正数

再将改正数与参数近似值相加，即得后方交会要求解的外方位元素的值。

迭代

通常情况下，按以上步骤求得的外方位元素改正数 X 太大，还不能满足实际需求，因此需要迭代。将第7步解得的外方位元素的值作为新的外方位元素近似值，代入第3步，再次开始计算。如此反复，直至外方位元素改正数 X 小于限差为止。通常对角元素设置限差，即

1.4 精度评定

按照上述方法求得的外方位元素，其精度可以通过法方程的系数矩阵的逆阵来求得，即

协因数阵 Q 的对角线上的元素 Qii 就是第 i 个未知数的权倒数。若单位权中误差为 m0 ，则第 i 个未知数的中误差为 [2] 。

当参加空间后方交会的控制点有 n 个时，单位权中误差可按下式计算：

2 问题求解

2.1 问题重述

已知摄影机主距 f=153.24mm，四对点的像点坐标与相应的地面点坐标如下表：

控制点号	像点x	像点y	物点X	物点Y	物点Z
1	-0.08615	-0.06899	36589.41	25273.32	2195.17
2	-0.05340	0.08221	37631.08	31324.51	728.69
3	-0.01478	-0.07663	39100.97	24934.98	2386.50
4	0.01046	0.06443	40426.54	30319.81	757.31

计算近似垂直摄影情况下的后方交会解。

2.2 问题解读与说明

1．注意单位的换算mm与m。

2．题目给的条件是近似垂直摄影测量，因此初始角度应该设为0，且应采用简化后的公式，不应画蛇添足（这里为了多做练习，采用未进行简化的式子）。

3．初始Z值的设置应为m*f 而不是简单的求平均值（否则会一直不收敛）。由于m值未给出，参照网上代码选取40000。

4．需要迭代计算的只有六个元素，其余变化皆为六个元素经变换等操作求出，迭代结束限差应先考虑角度，再是Z，最后是XY。

5．注意：这里由于共线方程式进行了简化，将x表示x-x0（这样求出来是零！不知道为什么！因此在求解时根据贡献方程式再一步转化成了-fX/Z和-fY/Z），计算误差公式的A矩阵求解所用的x并不是像点坐标。

6．求逆矩阵采用代数余子式法，利用递归方法，时间复杂度较高，不能用于大数据的计算，LUV分解法相对省时间，但是我不太会= =。动态申请二维数组可以定义长度不定的数组空间，但是定义较为麻烦。

2.3 c语言求解实现代码

/*
---------------------------------------------------------------------
	空间后方交会代码

	时间：2019年11月1日 

	步骤：1.先设置初值
	2.再用间接平差法求得改正值
	3.用改正值加上初始值进行迭代操作，满足限差要求时退出
	4.最后进行精度评价

	参考网址：http://www.docin.com/p-641460791.html
	矩阵求逆 https://cloud.tencent.com/developer/article/1359605
--------------------------------------------------------------------
*/
#include 
#include 
#include 

#define GCPNUMBER 4		//设置初始值控制点数量
#define N 6

int main()
{
	int i, j, k;
	int repeatNumber = 0;	//迭代次数
	int m = 40000;	//比例尺
	double x0=0,y0=0,f = 0.15324;	//内方位元素
	double dOuterElem[6] = { 1,1,1,1,1,1 };
	double outerElement[6] = { 0.0 };	//要求的参数:Xs,Ys,Zs,fai,omiga,kaba;
	//输入控制点空间坐标和像坐标xy和XYZ
	double GCPLocationxy [GCPNUMBER][2] = {		//控制点像坐标
		{ -0.08615, -0.06899 },
		{ -0.05340, 0.08221 }, 
		{ -0.01478, -0.07663 }, 
		{ 0.01046, 0.06443 } };	
	double GCPLocationXYZ [GCPNUMBER][3] = {	//控制点物空间坐标
		{ 36589.41, 25273.32, 2195.17 },
		{ 37631.08, 31324.51, 728.69 },
		{ 39100.97, 24934.98, 2386.50 },
		{ 40426.54, 30319.81, 757.31 } };
	printf("单像空间后方交会：\n\n");
	printf("已知条件：\n\n");
	printf("  比例尺：\n      m = %d\n\n", m);
	printf("  内方位元素：\n     x0 = %lf   y0 = %lf   f = %lf\n\n", x0, y0, f);
	printf("  控制点像坐标：\n");
	for (i = 0; i < GCPNUMBER; i++)
	{
		printf("     ");
		for (j = 0; j < 2; j++)
		{
			printf("%lf   ", GCPLocationxy[i][j]);
		}
		printf("\n");
	}
	printf("\n  控制点物空间坐标：\n");
	for (i = 0; i < GCPNUMBER; i++)
	{
		printf("     ");
		for (j = 0; j < 3; j++)
		{
			printf("%lf   ", GCPLocationXYZ[i][j]);
		}
		printf("\n");
	}
	printf("\n迭代过程：");
	//给外方位元素赋初值
	double sumXYZ[3] = { 0.0 };
	for (i = 0; i < 3; i++)
	{
		for (j = 0; j < GCPNUMBER; j++)
		{
			sumXYZ[i] += GCPLocationXYZ[j][i];
		}
		for (j = 0; j < 2;j++)
			outerElement[i] = sumXYZ[i] / GCPNUMBER;	//XY为四个控制点取平均值
		outerElement[i] = m*f + sumXYZ[i] / GCPNUMBER;		//Z为m*f
	}

	bool GetMatrixInverse(double **src, int n, double des[N][N]);	//求逆矩阵声明
	do	//迭代过程
	{
		double R[3][3] = { 0.0 };	//旋转矩阵R
		R[0][0] = cos(outerElement[3])*cos(outerElement[5]) - sin(outerElement[3])*sin(outerElement[4])*sin(outerElement[5]);
		R[0][1] = -cos(outerElement[3])*sin(outerElement[5]) - sin(outerElement[3]) * sin(outerElement[4])*cos(outerElement[5]);
		R[0][2] = -sin(outerElement[3])*cos(outerElement[4]);
		R[1][0] = cos(outerElement[4])*sin(outerElement[5]);
		R[1][1] = cos(outerElement[4])*cos(outerElement[5]);
		R[1][2] = -sin(outerElement[4]);
		R[2][0] = sin(outerElement[3])*cos(outerElement[5]) + cos(outerElement[3])*sin(outerElement[4])*sin(outerElement[5]);
		R[2][1] = -sin(outerElement[3])*sin(outerElement[5]) + cos(outerElement[3])*sin(outerElement[4])*cos(outerElement[5]);
		R[2][2] = cos(outerElement[3])*cos(outerElement[4]);

		double Xgang[GCPNUMBER];
		for (i = 0; i < GCPNUMBER; i++)
			Xgang[i] = R[0][0] * (GCPLocationXYZ[i][0] - outerElement[0]) + R[1][0] * (GCPLocationXYZ[i][1] - outerElement[1])
			+ R[2][0] * (GCPLocationXYZ[i][2] - outerElement[2]);
		double Ygang[GCPNUMBER];
		for (i = 0; i < GCPNUMBER; i++)
			Ygang[i] = R[0][1] * (GCPLocationXYZ[i][0] - outerElement[0]) + R[1][1] * (GCPLocationXYZ[i][1] - outerElement[1])
			+ R[2][1] * (GCPLocationXYZ[i][2] - outerElement[2]);
		double Zgang[GCPNUMBER];
		for (i = 0; i < GCPNUMBER; i++)
			Zgang[i] = R[0][2] * (GCPLocationXYZ[i][0] - outerElement[0]) + R[1][2] * (GCPLocationXYZ[i][1] - outerElement[1])
			+ R[2][2] * (GCPLocationXYZ[i][2] - outerElement[2]);
		
		//xy作为初始值，由共线方程式子求得
		double approxxy[GCPNUMBER][2] = { 0.0 };
		for (i = 0; i < GCPNUMBER; i++)
		{
			approxxy[i][0] = -f*Xgang[i] / Zgang[i];
			approxxy[i][1] = -f*Ygang[i] / Zgang[i];
			//用下面的数据求结果等于零，不知道为什么
			//approxxy[i][0] = GCPLocationxy[i][0]-x0;
			//approxxy[i][1] = GCPLocationxy[i][1] - y0;
		}

		//误差方程式元素A
		double A[GCPNUMBER * 2][6];
		for (i = 0; i < GCPNUMBER; i++)
		{
			A[i * 2][0] = (R[0][0] * f + R[0][2] * approxxy[i][0]) / Zgang[i];
			A[i * 2][1] = (R[1][0] * f + R[1][2] * approxxy[i][0]) / Zgang[i];
			A[i * 2][2] = (R[2][0] * f + R[2][2] * approxxy[i][0]) / Zgang[i];
			A[i * 2][3] = (approxxy[i][0] * approxxy[i][1])*R[1][0] / f - (f + pow(approxxy[i][0], 2) / f)*R[1][1] - approxxy[i][1] * R[1][2];
			A[i * 2][4] = -pow(approxxy[i][0], 2)*sin(outerElement[5]) / f - (approxxy[i][0] * approxxy[i][1]) / f*cos(outerElement[5]) - f*sin(outerElement[5]);
			A[i * 2][5] = approxxy[i][1];
			A[i * 2 + 1][0] = (R[0][1] * f + R[0][2] * approxxy[i][1]) / Zgang[i];
			A[i * 2 + 1][1] = (R[1][1] * f + R[1][2] * approxxy[i][1]) / Zgang[i];
			A[i * 2 + 1][2] = (R[2][1] * f + R[2][2] * approxxy[i][1]) / Zgang[i];
			A[i * 2 + 1][3] = -(approxxy[i][0] * approxxy[i][1])*R[1][1] / f + (f + pow(approxxy[i][1], 2) / f)*R[1][0] - approxxy[i][0] * R[1][2];
			A[i * 2 + 1][4] = -pow(approxxy[i][1], 2)*cos(outerElement[5]) / f - (approxxy[i][0] * approxxy[i][1]) / f*cos(outerElement[5]) - f*sin(outerElement[5]);
			A[i * 2 + 1][5] = -approxxy[i][0];
		}
		
		//误差方程式元素L
		double L[GCPNUMBER * 2];
		for (i = 0; i < GCPNUMBER * 2; i++)
		{
			if (i % 2 == 0)	//x
				L[i] = GCPLocationxy[i / 2][0] - approxxy[i / 2][0];
			else
				L[i] = GCPLocationxy[i / 2][1] - approxxy[i / 2][1];
		}
		//求转置
		double AT[6][GCPNUMBER * 2];
		for (i = 0; i < 6; i++)
		{
			for (j = 0; j < GCPNUMBER * 2; j++)
			{
				AT[i][j] = A[j][i];
			}
		}
		//求Naa
		double **Naa=new double*[6];
		//----------------------------动态申请数组-----------------------------
		for(i=0;i<6;i++)
		{
			Naa[i]=new double[6];
		}
		for (int i = 0; i < 6; i++)
		{
			for (int j = 0; j < 6; j++)
			{
				Naa[i][j] = 0.0;
			}
		};
		//-------------------------上面步骤的可以用 double Naa[6][6]={0.0}; 等效替代-----------------
		for (i = 0; i < 6; i++)
		{
			for (j = 0; j < 6; j++)
			{
				for (k = 0; k < GCPNUMBER * 2; k++)
				{
					Naa[i][j] += AT[i][k] * A[k][j];	//计算Naa
				}
			}
		}
		//求Naa逆矩阵
		double NaaInv[6][6] = { 0.0 };
		bool inverse = GetMatrixInverse(Naa, N, NaaInv);

		//求ATL
		double temp[6] = { 0.0 };
		for (i = 0; i < 6; i++)	//行遍历
		{
			for (j = 0; j < GCPNUMBER * 2; j++)
			{
				temp[i] += AT[i][j] * L[j];
			}
		}
		//求三角号
		for (i = 0; i < 6; i++)
		{
			dOuterElem[i] = 0.0;
			for (j = 0; j < 6; j++)
			{
				dOuterElem[i] += NaaInv[i][j] * temp[j];
			}
		}
		//求得迭代后的改正值及迭代后的外方位元素
		printf("\n\n  第%d次迭代改正值：\n     ", ++repeatNumber);
		for (i = 0; i < 6; i++)
		{
			printf("%lf     ", dOuterElem[i]);
			outerElement[i] = outerElement[i] + dOuterElem[i];
		}
		printf("\n  迭代后外方位元素值：\n     ");
		for (i = 0; i < 6; i++)
		{
			printf("%lf     ", outerElement[i]);
		}
	}while (dOuterElem[3] >= 2.908882087e-5 || dOuterElem[4] >= 2.908882087e-5 || dOuterElem[5] >= 2.908882087e-5);//各角元素迭代计算至其改正值小于6秒,6s=2.908882087e-5 弧度。

	//精度评价
	printf("\n\n\n精度评价矩阵：\n");
	//double sum[6] = { 0.0 };
	double outElemAccuracy[6][6] = { 0.0 };
	for (j = 0; j < 6; j++)
	{
		printf("     ");
		for (i = 0; i < 6; i++)
		{
			outElemAccuracy[j][i] = sqrt(abs(dOuterElem[j] * dOuterElem[i]) / double(2 * GCPNUMBER - 6));
			printf("%lf   ", outElemAccuracy[j][i]);
		}
		printf("\n");
	}
	system( "pause" );
}

/*
	以下为求逆矩阵函数：
	方法：代数余子式乘行列式倒数法
	代数余子式用迭代方法完成，行列式也用代数余子式
	按第一行展开计算|A|
	输入要求逆的矩阵和矩阵行列数
*/
double getA(double **arcs , int n)
{
	int i,j,k;
	if (n == 1)
		return arcs[0][0];
	double ans = 0;
	//double temp[N][N] = { 0.0 };
	double **temp=new double *[n-1];
	for(i=0;i<n-1;i++)
	{
		temp[i]=new double[n-1];
	}	
	for (int i = 0; i < n-1; i++)
	{
		for (int j = 0; j < n-1; j++)
		{
			temp[i][j]=0.0;
		}
	}
	for (i = 0; i < n; i++)	//第一行进行遍历
	{
		//其他行列组成矩阵，求代数余子式
		for (j = 0; j < n - 1; j++)
		{
			for (k = 0; k < n - 1; k++)
			{
				temp[j][k] = arcs[j + 1][(k >= i) ? k + 1 : k];
				//printf("%lf  ",temp[j][k]);
			}
		}
		//printf("暂时的------");
		double t = getA(temp, n - 1);

		if (i % 2 == 0)
		{
			ans += arcs[0][i] * t;	//结果：t是代数余子式，arcs【0】【i】是第一行的数字
		}
		else
		{
			ans -= arcs[0][i] * t;
		}
	}
	return ans;
}
//计算每一行每一列的每一个元素所对应的余子式，组成A*
void getAStart(double **arcs, int n, double ans[N][N])
{
	if (n == 1)		//如果是一阶行列式
	{
		ans[0][0] = 1;
		return;
	}
	int i, j, k, t;
	//double temp[N][N];
	double **temp=new double*[N];
	for (i = 0; i<n - 1; i++)
	{
		temp[i] = new double[n - 1];
	}
	for (int i = 0; i < n - 1; i++)
	{
		for (int j = 0; j < n - 1; j++)
		{
			temp[i][j] = 0.0;
		}
	}
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < n; j++)
		{
			//每一个矩阵元素的代数余子式
			for (k = 0; k < n - 1; k++)
			{
				for (t = 0; t < n - 1; t++)
				{
					temp[k][t] = arcs[k >= i ? k + 1 : k][t >= j ? t + 1 : t];
				}
			}
			ans[j][i] = getA(temp, n - 1);
			if ((i + j) % 2 == 1)
			{
				ans[j][i] = -ans[j][i];
			}
		}
	}
	delete temp;
}

//得到给定矩阵src的逆矩阵保存到des中
bool GetMatrixInverse(double **src, int n, double des[N][N])
{
	double flag = getA(src, n);	//|A|
	double t[N][N];
	if (0 == flag)
	{
		printf( "原矩阵行列式为0，无法求逆。请重新运行" );
		return false;
	}
	else
	{
		getAStart(src, n, t);	//求代数余子式
		//求逆矩阵
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < n; j++)
			{
				des[i][j] = t[i][j] / flag;
			}
		}
	}
	return true;
}

2.4 程序评价

优点：代码注释全面，输出结果清晰明了，对读代码者较为友好；对于不同的控制点数量只需要更改GCPNUMBER变量即可，无需改变内部函数；用动态申请数组，可以节省部分空间。

缺点：未进行函数的包装，将其过程一股脑扔到了main函数中，显得没有条理；过多使用for循环和数组，感觉程序很臃肿；未进行相似函数的封装（譬如说矩阵乘法）为了省事就直接计算了。