SVM —— 代码实现

SMO 算法的实现步骤：

代码如下：

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import random


# 设置中文字体为宋体，英文字体为 times new roman
sns.set(font="SimSun", style="ticks", font_scale=1.2)


# 读取数据
def read_dataset(file_path: str) -> (list, list):
    """
    :param file_path: 存放了样本数据的文件路径
    :return: 样本特征数据列表，样本标签列表
    """
    data_list = []
    label_list = []

    file = open(file_path)
    for line in file.readlines():
        line = line.strip().split('\t')
        data_list.append([float(line[0]), float(line[1])])  # 添加样本特征数据
        label_list.append(float(line[2]))  # 添加样本标签
    file.close()

    return data_list, label_list


# 可视化样本数据
def visual_dataset(data_list: list, label_list: list) -> None:
    """
    :param data_list: 样本特征数据列表
    :param label_list: 样本标签列表
    :return: None
    """
    data_positive = []  # 存放正样本数据
    data_negtive = []  # 存放负样本数据

    for i in range(len(data_list)):
        if label_list[i] > 0:
            data_positive.append(data_list[i])
        else:
            data_negtive.append(data_list[i])

    data_positive_arr = np.array(data_positive)
    data_negtive_arr = np.array(data_negtive)

    # 可视化，第一列特征数据作为 x（x1）轴，第二列特征数据作为 y（x2）轴
    plt.scatter(np.transpose(data_positive_arr)[0], np.transpose(data_positive_arr)[1], marker='o', color='red')  # 正样本散点图
    plt.scatter(np.transpose(data_negtive_arr)[0], np.transpose(data_negtive_arr)[1], marker='s', color='green')  # 负样本散点图
    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.legend(['positive', 'negtive'], loc='lower right')
    plt.title('样本数据分布')
    plt.show()


# 随机选择一个不等于 i 的 j
def random_select_lambda(i: int, m: int) -> int:
    """
    :param i: 索引
    :param m: 样本数
    :return: 不等于 i 的索引
    """
    j = i
    while j == i:
        j = int(random.uniform(0, m))

    return j


# 修剪 lambda
def clip_lambda(lambda_j: float, H: float, L: float) -> float:
    """
    :param lambda_j: 索引为 j 的 lambda 值
    :param H: 边界 H
    :param L: 边界 L
    :return: 新的索引为 j 的 lambda 值
    """
    if lambda_j > H:
        lambda_j = H
    if lambda_j < L:
        lambda_j = L

    return lambda_j


# 简化版 SMO 算法
def simplified_smo(data_list: list, label_list: list, slack_variable: float, C: float, max_iteration: int) -> (np.ndarray, float):
    """
    :param data_list: 样本特征数据列表
    :param label_list: 样本标签列表
    :param slack_variable: 松弛变量
    :param C: 惩罚参数
    :param max_iteration: 最大迭代次数
    :return: 参数矩阵 lambdas，参数 b
    """
    data_mat = np.mat(data_list)  # 转换为矩阵；(100, 2)
    label_mat = np.mat(label_list).transpose()  # 转换为矩阵；(100, 1)

    m, n = np.shape(data_mat)  # 获取 data_mat 的行数和列数，行代表样本，列代表特征

    b = 0  # 初始化参数 b

    lambdas = np.mat(np.zeros((m, 1)))  # 初始化每个样本的 lambda 参数，并转换为矩阵；(100, 1)

    num_iteration = 0  # 初始化迭代次数

    while (num_iteration < max_iteration):
        lambda_pairs_changed = 0  # 初始化优化次数变量
        for i in range(m):
            # 步骤1，计算误差 Ei
            func_fxi = float(np.multiply(lambdas, label_mat).T * (data_mat * data_mat[i, :].T)) + b
            Ei = func_fxi - float(label_mat[i])

            # 优化 lambda
            if ((label_mat[i] * Ei < -slack_variable) and (lambdas[i] < C)) or ((label_mat[i] * Ei > slack_variable) and (lambdas[i] > 0)):
                j = random_select_lambda(i, m)  # 随机选择一个与 lambda_i 成对优化的 lambda_j

                # 步骤1，计算误差 Ej
                func_fxj = float(np.multiply(lambdas, label_mat).T * (data_mat * data_mat[j, :].T)) + b
                Ej = func_fxj - float(label_mat[j])

                # 保存更新前的 lambda_i、lambda_j 值
                lambda_i_old = lambdas[i].copy()
                lambda_j_old = lambdas[j].copy()

                # 步骤2，计算上下界 L 和 H
                L, H = 0.0, 0.0
                if label_mat[i] != label_mat[j]:
                    L = max(0, lambdas[j] - lambdas[i])
                    H = min(C, C + lambdas[j] - lambdas[i])
                else:
                    L = max(0, lambdas[j] + lambdas[i] - C)
                    H = min(C, lambdas[j] + lambdas[i])

                if L == H:
                    print('L == H')
                    continue

                # 步骤3，计算 eta
                eta = 2.0 * data_mat[i, :] * data_mat[j, :].T - data_mat[i, :] * data_mat[i, :].T - data_mat[j, :] * data_mat[j, :].T

                if eta >= 0:
                    print('eta >= 0')
                    continue

                # 步骤4，更新 lambda_j
                lambdas[j] -= label_mat[j] * (Ei - Ej) / eta

                # 步骤5，修剪 lambda_j
                lambdas[j] = clip_lambda(lambdas[j], H, L)

                if abs(lambdas[j] - lambda_j_old) < 0.00001:
                    print('lambda_j 变化太小')
                    continue

                # 步骤6，更新 lambda_i
                lambdas[i] += label_mat[i] * label_mat[j] * (lambda_j_old - lambdas[j])

                # 步骤7，更新 b1 和 b2
                b1 = b - Ei - label_mat[i] * (lambdas[i] - lambda_i_old) * (data_mat[i, :] * data_mat[i, :].T) - label_mat[j] * (lambdas[j] - lambda_j_old) * (data_mat[i, :] * data_mat[j, :].T)
                b2 = b - Ej - label_mat[i] * (lambdas[i] - lambda_i_old) * (data_mat[i, :] * data_mat[j, :].T) - label_mat[j] * (lambdas[j] - lambda_j_old) * (data_mat[j, :] * data_mat[j, :].T)

                # 步骤8，根据 b1、b2 更新 b
                if (lambdas[i] > 0) and (lambdas[i] < C):
                    b = b1
                elif (lambdas[j] > 0) and (lambdas[j] < C):
                    b = b2
                else:
                    b = (b1 + b2) / 2.0

                lambda_pairs_changed += 1  # 统计优化次数

                print('第 %d 次迭代 === 第 %d 个样本 === 第 %d 次 lambda 优化' % (num_iteration, i, lambda_pairs_changed))

        # 更新迭代次数
        if lambda_pairs_changed == 0:
            num_iteration += 1
        else:
            num_iteration = 0

    return lambdas, b


# 计算参数 w
def get_w(data_list: list, label_list: list, lambdas: np.ndarray) -> list:
    """
    :param data_list: 样本特征数据列表
    :param label_list: 样本标签列表
    :param lambdas: 各样本的参数 lambda 矩阵
    :return: 参数 w 列表
    """
    data_arr, label_arr, lambdas_arr = np.array(data_list), np.array(label_list), np.array(lambdas)
    w = np.dot((np.tile(label_arr.reshape(1, -1).T, (1, 2)) * data_arr).T, lambdas_arr)

    return w.tolist()


# 可视化分类结果
def visual_classification_result(data_list: list, w: list, b: float, lambdas) -> None:
    """
    :param data_list: 样本特征数据列表
    :param w: 参数 w 列表
    :param b: 参数 b
    :return: None
    """
    data_positive = []  # 存放正样本数据
    data_negtive = []  # 存放负样本数据

    for i in range(len(data_list)):
        if label_list[i] > 0:
            data_positive.append(data_list[i])
        else:
            data_negtive.append(data_list[i])

    data_positive_arr = np.array(data_positive)
    data_negtive_arr = np.array(data_negtive)

    # 可视化，第一列特征数据作为 x（x1）轴，第二列特征数据作为 y（x2）轴
    # 绘制散点图
    plt.scatter(np.transpose(data_positive_arr)[0], np.transpose(data_positive_arr)[1], marker='o', color='blue', s=50, alpha=0.7)  # 正样本散点图
    plt.scatter(np.transpose(data_negtive_arr)[0], np.transpose(data_negtive_arr)[1], marker='s', color='pink', s=50, alpha=0.7)  # 负样本散点图

    # 绘制直线
    x_left = min(data_list)[0]
    x_right = max(data_list)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    y_left = (-b - a1 * x_left) / a2
    y_right = (-b - a1 * x_right) / a2
    plt.plot([x_left, x_right], [y_left, y_right])

    # 找出支持向量，并绘制其散点图
    for i, lam in enumerate(lambdas):
        if lam > 0:
            x, y = data_list[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, edgecolors='red')

    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.legend(['positive', 'negtive'], loc='lower right')
    plt.title('最大间隔超平面可视化')
    plt.show()


if __name__ == '__main__':
    file_path = r'D:\MachineLearning\testSet.txt'

    # 读取数据，返回样本特征数据列表和样本标签列表
    data_list, label_list = read_dataset(file_path)

    # 可视化样本数据
    visual_dataset(data_list, label_list)

    # SMO 算法
    lambdas, b = simplified_smo(data_list, label_list, 0.001, 0.6, 40)

    # 获取参数 w
    w = get_w(data_list, label_list, lambdas)

    # 可视化分类结果
    visual_classification_result(data_list, w, b, lambdas)

核技巧

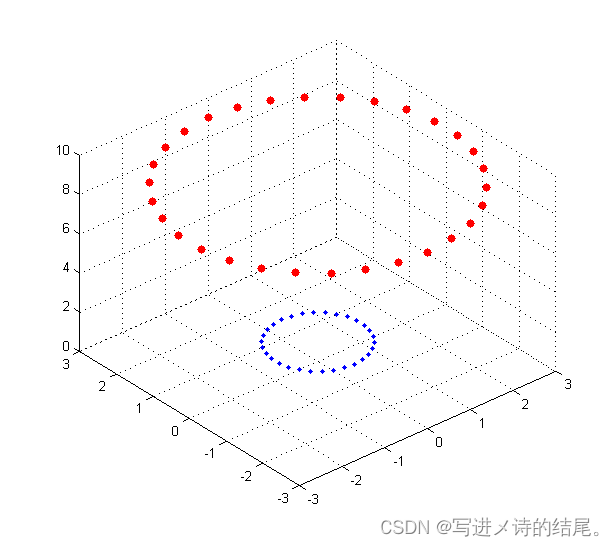
为什么要使用核技巧呢？假设二维平面上存在若干点，其中点集 A 服从 $\left\{x,y|x^2+y^2=1\right\}$，点集 B 服从 $\left\{x,y|x^2+y^2=9\right\}$，它们在平面上的分布如下图所示：

蓝色为点集 A，红色为点集 B，它们在二维平面中并不线性可分。如果采用映射的方法，将 $(x,y)\to (x,y,x^2+y^2)$，这些点在三维空间中的分布如下图所示：

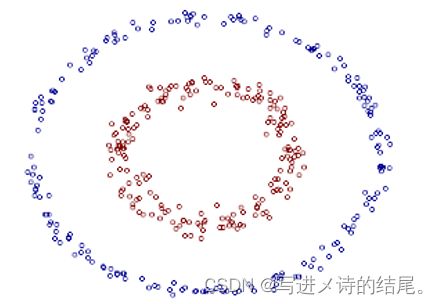
蓝色点集 A 和红色点集 B 被映射到了不同的平面，这说明它们在更高维的空间中可以实现线性可分（用一个平面进行分隔）。上述样本点遵循圆的分布，如果我们将其推广到椭圆，如下图所示：

上图中，两类数据的分布形似椭圆，很明显这样的样本点是线性不可分的。能将两类样本点完全分隔开的理想的分界线应该也是一个椭圆，而不是一条直线。如果用 $X_1、X_2$ 来表示二维平面两个坐标的话，这个椭圆分界线的公式就可以写成如下：
$$a_1{X}_1+a_2{X}_1^2+a_3{X}_2+a_4{X}_2^2+a_5{X}_1{X}_2+a_6=0$$
这个方程是中学就学过的椭圆的一般方程。如果我们构造一个五维空间，五个坐标的值分别为：
$$Z_1=X_1,Z_2=X_1^2,Z_3=X_2,Z_4=X_2^2,Z_5=X_1{X}_2$$
那么显然，我们可以将上述椭圆方程写成如下形式：
$$\sum _{i=1}^5{a}_i{Z}_i+a_6=0$$
这是一个关于变量 $Z_i$ 的超平面方程，维度为 5。也就是说，当我们做一个映射，将样本点从二维空间映射到五维空间，从而使得样本点在新的高维空间中线性可分，那么就可以用之前推导的线性 SVM 分类方法来进行处理了。

举个简单的例子，对于两个向量 $a=(x_1,x_2)$ 和 $b=(y_1,y_2)$，如果使用核技巧，不进行映射计算，则直接运算以下公式：
$$(<x_1,x_2>+1{)}^2=2x_1{y}_1+x_1^2{y}_1^2+2x_2{y}_2+x_2^2{y}_2^2+2x_1{x}_2{y}_1{y}_2+1$$
其中，$<\cdot >$ 表示内积。

如果不使用核技巧，则需先进行映射，将样本点从低维空间映射到高维空间，再进行内积运算：
$$<\varphi (x_1,x_2),\varphi (y_1,y_2)>=2x_1{y}_1+x_1^2{y}_1^2+2x_2{y}_2+x_2^2{y}_2^2+2x_1{x}_2{y}_1{y}_2+1$$
其中，$\varphi (x_1,x_2)=(\sqrt{2}{x}_1,x_1^2,\sqrt{2}{x}_2,x_2^2,\sqrt{2}{x}_1{x}_2,1)$。

可以发现，两种计算方式的结果是一样的，但是区别在哪呢？区别在于：

• 如果不使用核技巧，则需要根据映射函数，将样本点从低维空间映射到高维空间，然后再计算内积，计算量大。
• 如果使用核技巧，则可以直接在低维空间中进行计算，计算量小。

在上述例子中，$(<x_1,x_2>+1{)}^2$ 就是核函数 $k(x_1,x_2)$。我们对一个 2 维空间做映射，得到 5 维空间，如果原始空间是 3 维的，那么映射后将得到 19 维的新空间，这个维数是呈爆炸式增长的。如果我们根据映射函数，对样本点做高维映射计算，难度将会非常大，一旦遇到无穷维的情况，甚至无法进行计算，因此使用核技巧是非常有必要的。

径向基核函数是 SVM 中常用的一个核函数，其高斯版本的公式如下：
$$k(x_1,x_2)=e^{-\frac{||x_1-x_2|{|}^2}{2{\sigma }^2}}$$
其中，$\sigma$ 是用户自定义的用于确定到达率或者说函数值跌落到 0 的速度参数。上述高斯核函数将数据从原始空间映射到无穷维空间。关于无穷维空间，我们不必太担心，高斯核函数只是一个常用的核函数，使用者并不需要确切地理解数据到底是如何表现的，而且使用高斯核函数还会得到一个理想的结果。如果 $\sigma$ 选的很大，高次特征上的权重会衰减得非常快，这样的话高维空间实际上就相当于一个低维的子空间；反过来，如果 $\sigma$ 选的很小，则可以将任意的数据映射为线性可分。当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。不过总的来说，通过调控参数 $\sigma$，高斯核能够具有相当高的灵活性，也是使用最广泛的核函数之一。

使用 sklearn 构建 SVM 分类器

sklearn.svm 模块提供了很多模型供我们使用，本文使用的是 sklearn.svm.SVC 算法，它是基于 libsvm 实现的。SVC 函数实现如下所示：

sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='scale', coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, random_state=None)
	- C：惩罚参数，即正则化参数，默认为 1.0；正则化强度与 C 的值成反比，C 越大，对错分样本的惩罚程度就越大，训练集的准确率高，但是泛华能力降低，测试集的准确率降低，也就是容易发生过拟合。减小 C，则容许训练样本中有一些错分样本，泛华能力提升
	- kernel：指定核函数类型，默认为 rbf；可选类型有 linear（线性核函数）、poly（多项式核函数）、rbf（径向基/高斯核函数）、sigmoid（sigmoid 核函数）、precomputed（核矩阵）；precomputed 表示提前计算好的核函数矩阵，如果选择这个，那么算法内部就不再用核函数去计算核矩阵了，而是直接用提前计算好的这个核矩阵
	- degree：多项式核函数的阶数，默认为 3；这个参数只对多项式核函数有用，如果选择的是其他类型的核函数，则会自动忽略该参数
	- gamma：核函数系数，有 scale、auto、float 可供选择，默认为 scale；只对 rbf、poly、sigmoid 核函数有用；如果为 scale，则使用 1/(n_features * X.var()) 作为 gamma 值；如果为 auto，则使用 1/n_features 作为 gamma 值；如果为 float，则必须是非负值
	- coef0：核函数中的独立项，只对 poly、sigmoid 核函数有用
	- shrinking：是否采用启发式收缩方式，默认为 True
	- probability：是否启用概率估计，默认为 False；这个必须在调用 fit() 之前启用，由于该方法内部会使用 5 倍交叉验证，因此会减慢速度
	- tol：SVM 停止训练的误差精度，默认为 1e-3
	- cache_size：指定缓存大小，默认为 200MB
	- class_weight：类别权重，默认为 None；给每个类别设置不同的惩罚参数 C，如果为 None，则给所有类别都设置 C=1
	- verbose：是否启用详细输出，默认为 False；该设置利用了 libsvm 中的一个按进程运行时设置，如果启用该设置，可能无法在多线程环境下正常运行
	- max_iter：最大迭代次数，默认为 -1，表示无限制
	- decision_function_shape：决策函数类型，可选择的有 ovo（one-vs-one）、ovr（one-vs-rest），默认为 ovr；对于二分类，该参数将被忽略
	- break_ties：默认为 False；如果为 true，decision_function_shape='ovr'，且类别数大于 2，predict 将根据 decision_function 的置信度值打破并列关系；否则将返回并列类别中的第一个类别。请注意，与简单的预测相比，打破并列关系的计算成本相对较高。
	- random_state：控制伪随机数生成，用于混洗数据时估计概率，默认为 None

由 SVC 创建的实例对象 clf 具有以下方法：

decision_function(X)  # 预测样本的置信度得分
	- X：训练数据，形状为 (n_samples, n_features)
	返回形状为 (n_samples, n_classes) 的置信度得分

fit(X, y, sample_weight=None)  # 根据训练集拟合分类器
	- X：训练数据，形状为 (n_samples, n_features)
    - y：目标值（训练样本对应的标签），形状为 (n_samples,)
    - sample_weight：样本权重，如果为 None，则样本权重相同
    返回拟合的 SVM 分类器

get_params(deep=True)  # 以字典形式返回 SVC 类的参数
	- deep：布尔值，默认为 True
    返回参数

predict(X)  # 预测所提供数据的类别标签
	- X：预测数据，形状为 (n_samples, n_features)
    以 np.ndarray 形式返回形状为 (n_samples,) 的每个数据样本的类别标签
    
predict_log_proba(X)  # 返回预测数据 X 在各类别标签中所占的对数概率
	- X：预测数据，形状为 (n_samples, n_features)
    返回该样本在各类别标签中的预测对数概率，类别的顺序与属性 classes_ 中的顺序一致
    
predict_proba(X)  # 返回预测数据 X 在各类别标签中所占的概率
	- X：预测数据，形状为 (n_samples, n_features)
    返回该样本在各类别标签中的预测概率，类别的顺序与属性 classes_ 中的顺序一致
    
score(X, y, sample_weight=None)  # 返回预测结果和标签之间的平均准确率
	- X：预测数据，形状为 (n_samples, n_features)
    - y：预测数据的目标值（真实标签）
    - sample_weight：默认为 None
    返回预测数据的平均准确率，相当于先执行了 self.predict(X)，而后再计算预测值和真实值之间的平均准确率