KMP算法

本节主要介绍KMP算法，将从：KMP算法解决的主要问题引出前缀，前缀表以及具体算法实现。

KMP算法解决的主要问题

KMP算法是由提出他的三位作者名字命名的，无其他具体含义。KMP算法主要解决问题是，在长文本串S中匹配目标模式串p的问题。

LeetCode-28.找出字符串中第一个匹配项的下标

首先我们看看这道题：给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回  -1。

在不了解KMP的情况下应该如何解决？

我们可以使用两层循环，外层循环寻找haystack中与needle串首相同的位置，然后再进入内层循环逐一比较，时间复杂度为O(n∗m)O(n*m)O(n∗m)，代码如下：

var strStr = function (haystack, needle) {
  for (let i = 0; i < haystack.length; i++) {
    if (haystack[i] !== needle[0]) continue;

    //i指向可能的下标;
    let p = i;
    let q = 0;
    while (p < haystack.length && q < needle.length) {
      if (haystack[p] === needle[q]) {
        p++;
        q++;
      } else {
        break;
      }
    }
    if (p - i + 1 > needle.length) {
      return i;
    }
  }
  return -1;
};

而KMP算法可以将这个问题的时间复杂度降低到O(m+n)O(m+n)O(m+n)，这需要借助前缀表来实现。

前缀表

在解释前缀表之前，我们要先知道前缀和后缀的定义:

• 前缀：包含首字母，但不包含尾字母的所有子串。例如：abcd的前缀就是：a,ab,abc
• 后缀：包含尾字母，但不包含首字母的所有子串。例如：abcd的后缀就是：d,cd,bcd

而前缀表是一个数组（next[]），他存储的是，针对串p中的每一个子串s([0,j]) ，s的最大前后缀相等的长度。

例如：abab ,我们做如下分析：

• 对于首字母，他既无前缀也无后缀，因此对应的前缀表中的长度为 0 .
• 接下来是ab，前缀为a ，后缀为b 无相等前后缀，长度为 0 .
• aba,前缀a,ab,后缀是a,ba,拥有相等前后缀a,长度为 1 .
• abab,前缀为a,ab,aba，后缀为b,ab,bab，拥有相等前后缀ab，长度为 2 .
• 因此有前缀表：next === [0,0,1,2];

有什么用呢？

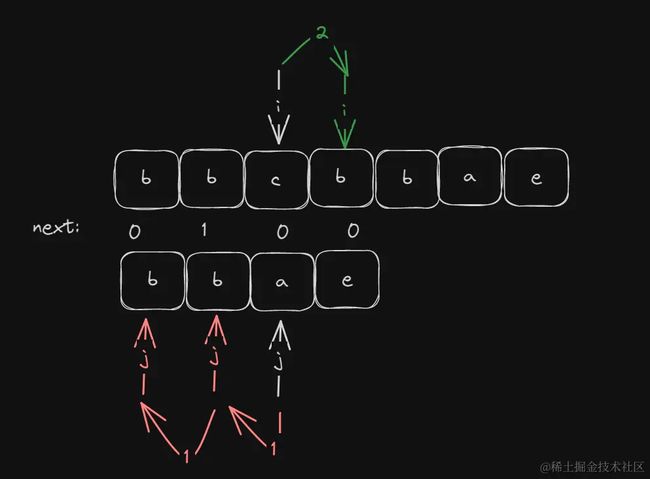
假设现在长文本串S为：bbcbbae，模式串p为：bbae。 我们求出前缀表next等于[0,1,0,0];如图：

当我们比较到c与a时，我们发现不相同，此时我们不再需要让bbae与bcbb去遍历比较了，而是将比较的位置进行回退，回退到当前不相等元素的前一个下标对应的next值，即此时是bb与bc比较，仍然不相等就继续回退，最终回退到首部或者相等。此时要比较的就是bbae与bbae了。

还是蛮抽象的：这里建议大家看下卡哥的讲解吧：KMP理论篇

我们目前知道了KMP算法能帮我们解决这个问题，那么问题就在于如何获得前缀表Next？

前缀表实现

我们使用双指针对模式串p进行遍历，其中指针i,j分别表示后缀末尾以及前缀末尾。

则有：

function getNext(pattern) {
  let j = 0; // 前缀末尾，也表示[0,i]子串的最长相同前后缀长度
  const next = [];
  next[0] = 0; // 第一个字符无前后缀，因此为0
  let i = 1; // 后缀末尾
  if (pattern.length <= 1) return next;
  for (; i < pattern.length; i++) {
    //匹配失败，前后缀不相同
    while (j > 0 && pattern[i] !== pattern[j]) {
      j = next[j - 1];
    }

    //匹配成功，即前后缀相同
    if (pattern[i] === pattern[j]) j++;
    next[i] = j;

  }
  return next;
}

接下来就是如何使用前缀表完成刚刚那道题了。

使用

var strStr = function (haystack, needle) {
  const next = getNext(needle);//获取前缀表

  for (let i = 0, j = 0; i < haystack.length; i++) {
    //j指向模式串，匹配失败就根据前缀表回退
    while (j > 0 && haystack[i] !== needle[j]) {
      j = next[j - 1];
    }
    if (haystack[i] === needle[j]) {
      j++;
    }
    //匹配成功
    if (j === needle.length) return i - needle.length + 1;
  }
  return -1;
};

扩展题目：LeetCode-459.重复的子字符串

给定一个非空的字符串 s ，检查是否可以通过由它的一个子串重复多次构成。

本题能使用KMP的原因是：字符串s的长度 % (字符串s的长度 - 最大前后缀相等长度) === 0 则代表该串可以由子串重复构成，此外(字符串s的长度 - 最大前后缀相等长度) 就是最小重复子串的长度

因此代码就很好写了：

var repeatedSubstringPattern = function (s) {
  const next = getNext(s);
  const len = s.length - next[next.length - 1];
  if (s.length % len === 0 && next[next.length - 1] !== 0) return true;
  return false;
};

KMP算法确实有点抽象，其抽象的点在于，我们计算前缀表时，实际上j总是在上一次比较的基础上进行计算的，所以你看不到使用循环去比较，而是匹配成功后j++。