5 剑指offer--栈队列--互相实现

                                      用两个栈实现队列

栈是一个非常常见的数据结构，它在计算机领域被广泛应用，比如操作系统会给每个线程创建一个栈用来存储函数调用时各个函数的参数、返回地址及临时变量等。桟的特点是后进先出，即最后被压 入 （push) 栈的元素会第一个被弹出（pop)。

通常栈是一个不考虑排序的数据结构，我们需要〇( n )时间才能找到栈中最大或者最小的元素。如果想要在0(1)时间内得到栈的最大值或者最小值，则需要对栈做特殊的设计，详见面试题3 0 “包含min函数的栈”。

队列是另外一种很重要的数据结构。和栈不同的是，队列的特点是先进先出，即第一个进入队列的兀素将会第一个出来。

栈和队列虽然是特点针锋相对的两个数据结构，但有意思的是它们却相互联系。读者也可以考虑如何用两个队列实现栈。

1 栈实现一个队列

题目：用两个栈实现一个队列。队列的声明如下，请实现它的两个函数appendTail 和deleteHead，分别完成在队列尾部插入结点和在队列头部删除结点的功能。

题目：用两个栈实现一个队列。队列的声明如下，请实现它的两个函数appendTail 和deleteHead，分别完成在队列尾部插入结点和在队列头部删除结点的功能。

分析

创建两个栈stack1和stack2，使用两个“先进后出”的栈实现一个“先进先出”的队列。

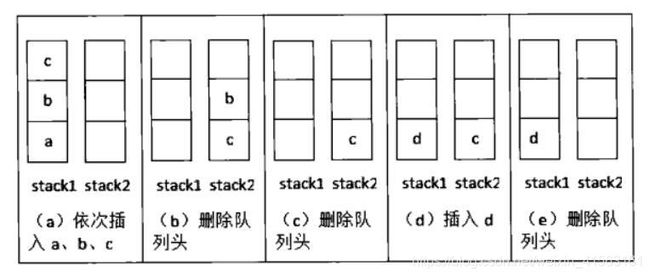
我们通过一个具体的例子分析往该队列插入和删除元素的过程。首先插入一个元素a，不妨先把它插入到stack1，此时stack1中的元素有{a}，stack2为空。再压入两个元素b和c，还是插入到stack1中，此时stack1的元素有{a,b,c}，其中c位于栈顶，而stack2仍然是空的。

这个时候我们试着从队列中删除一个元素。按照先入先出的规则，由于a比b、c先插入队列中，最先删除的元素应该是a。元素a存储在stack1中，但并不在栈顶，因此不能直接进行删除操作。注意stack2我们一直没有使用过，现在是让stack2发挥作用的时候了。如果我们把stack1中的元素逐个弹出压入stack2，元素在stack2中的顺序正好和原来在stack1中的顺序相反。因此经过3次弹出stack1和要入stack2操作之后，stack1为空，而stack2中的元素是{c,b,a}，这个时候就可以弹出stack2的栈顶a了。此时的stack1为空，而stack2的元素为{b,a}，其中b在栈顶。

因此我们的思路是：当stack2中不为空时，在stack2中的栈顶元素是最先进入队列的元素，可以弹出。如果stack2为空时，我们把stack1中的元素逐个弹出并压入stack2。由于先进入队列的元素被压倒stack1的栈底，经过弹出和压入之后就处于stack2的栈顶，有可以直接弹出。如果有新元素d插入，我们直接把它压入stack1即可。

流程示意图：

LeetCode描述

使用栈实现队列的下列操作：

push(x) -- 将一个元素放入队列的尾部。

pop() -- 从队列首部移除元素。

peek() -- 返回队列首部的元素。

empty() -- 返回队列是否为空。

示例:

MyQueue queue = new MyQueue();

queue.push(1);

queue.push(2); 

queue.peek();  // 返回 1

queue.pop();   // 返回 1

queue.empty(); // 返回 false

说明:

你只能使用标准的栈操作 -- 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。

你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）。

代码

import java.util.Deque;
import java.util.LinkedList;

public class 用两个栈实现队列 {
    Deque stack1 = new LinkedList<>();
    Deque stack2 = new LinkedList<>();

    public void push(int node) {
        stack1.addFirst(node);
    }

    public int pop() {
        if(stack1.isEmpty() && stack2.isEmpty()){
            System.out.println("有异常");
            throw new RuntimeException("有异常");
        }else if(stack2.isEmpty()){
            while(!stack1.isEmpty()){
                stack2.addFirst(stack1.removeFirst());
            }
            return stack2.removeFirst();
        }else{
            return stack2.removeFirst();
        }
    }
}

import java.util.Stack;

public class Solution {
    Stack stack1 = new Stack();
    Stack stack2 = new Stack();
    
    public void push(int node) {
        stack1.push(node);
    }

    public int pop() {
        if(stack1.isEmpty() && stack2.isEmpty()){
            System.out.println("有异常");
            throw new RuntimeException("有异常");
        }else if(stack2.isEmpty()){
            while(!stack1.isEmpty()){
                stack2.push(stack1.pop());
            }
            return stack2.pop();
        }else{
            return stack2.pop();
        }
    }
}

import java.util.Stack;

/**
 * @Auther: liuhaidong
 * Data: 2019/10/10 0010、17:44
 * Description:
 * @version: 1.0
 */
public class MyQueue {
    private Stack s1 ;
    private Stack s2;
    private int front;
    /** Initialize your data structure here. */
    public MyQueue() {
        s1 = new Stack<>();
        s2 = new Stack<>();
    }

    /** Push element x to the back of queue. */
    public void push(int x) {
        s1.push(x);
    }

    /** Removes the element from in front of queue and returns that element. */
    public int pop() {
        if (s1.isEmpty() && s2.isEmpty()) {
            throw new RuntimeException("Queue is empty.");
        }else if(s2.isEmpty()){
                //把第一个栈中的数据转到第二个栈中;
                while(!s1.empty()){
                    s2.push(s1.pop());
                }
            }
        return s2.pop();
        //如果第二个没有就直接弹出
    }

    /** Get the front element. */
    public int peek() {
        if(s1.empty() && s2.empty()) {
            throw new RuntimeException("queue is empty");
        }else if(s2.isEmpty()){
            //stackPop 必须为空才可以;
            while(!s1.empty()){
                s2.push(s1.pop());
            }
        }
        return s2.peek();
    }

    /** Returns whether the queue is empty. */
    public boolean empty() {
        if(s1.empty() && s2.empty()){
            return true;
        }
        return false;
    }
}

用队列实现栈

LettCode描述

使用队列实现栈的下列操作：

push(x) -- 元素 x 入栈

pop() -- 移除栈顶元素

top() -- 获取栈顶元素

empty() -- 返回栈是否为空

注意:

你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。

你所使用的语言也许不支持队列。 你可以使用 list 或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

你可以假设所有操作都是有效的（例如, 对一个空的栈不会调用 pop 或者 top 操作）。

思路

• 由于队列有先入先出的特性，所以当队列一存入数值需要弹出栈顶元素C时将队列元素个数减一的所有元素存入队列2同时队列1中元素出队，实现一个后入先出，以此左右往复直到队列为空，抛出异常。

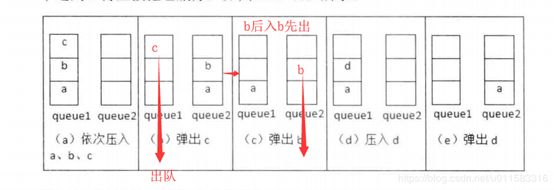
我们通过一系列栈的压入和弹出操作来分析用两个队列模拟一个栈的过程。如图(a) 所示，我们先往栈内压入一个元素a。由于两个队列现在都是空的，我们可以选择把a 插入两个队列的任意一个。我们不妨把a插 入 queuel。接下来继续往栈内压入b、c 两个元素，我们把它们都插入queuel。这个时候queuel包含3 个元素a、b 和 c，其中a 位于队列的头部，

c 位于队列的尾部。现在我们考虑从栈内弹出一个元素。根据栈的后入先出原则，最后被

压入桟的c 应该最先被弹出。由于c 位于queuel的尾部，而我们每次只能从队列的头部删除元素，因此我们可以先从queuel中依次删除元素a、b并插入queue2，再从queuel中删除元素c。这就相当于从栈中弹出元素c了，如图(b) 所示。我们可以用同样的方法从栈内弹出元素b，如图  (c) 所示。

接下来我们考虑往栈内压入一个元素d。此时queuel已经有一个元素,我们就把d 插入queue]的尾部，如图(d) 所示。如果我们再从栈内弹出一个元素，那么此时被弹出的应该是最后被压入的d。由于d 位于queuel的尾部，我们只能先从头删除queuel的元素并插入queue2 , 直到在queuel中遇到d 再直接把它删除，如图(e) 所示。

算法图解

代码

import java.util.LinkedList;
import java.util.Queue;

/**
 * @Auther: liuhaidong
 * Data: 2019/10/10 0010、17:46
 * Description:
 * @version: 1.0
 */
public class MyStack {
    /** Initialize your data structure here. */
    private Queue queue1;
    private Queue queue2;
    public MyStack() {
        queue1 = new LinkedList<>();
        queue2 = new LinkedList<>();
    }

    /** Push element x onto stack. */
    public void push(int x) {
        queue1.offer(x);
    }

    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        while (queue1.size() !=1){
            queue2.offer(queue1.poll());
        }
        int temp = queue1.poll();
        //把这最后一个保存下来
        while (queue2.size() != 0) {
            queue1.offer(queue2.poll());
        }
        //然后再把第二个里面的保持到第一个里面
        return temp;
    }

    /** Get the top element. */
    public int top() {
        while (queue1.size() != 1) {
            queue2.offer(queue1.poll());
        }
        return queue1.peek();
    }

    /** Returns whether the stack is empty. */
    public boolean empty() {
        return queue1.size() == 0;
    }
}