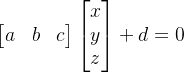支持向量机之超平面理解

 支持向量机（SVM，也叫支持向量网络），是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。是由Vapnik与同事（Boser等，1992；Guyon等，1993；Vapnik等，1997）在AT＆T贝尔实验室开发。支持向量机是基于统计学习框架与由Chervonenkis（1974）和Vapnik（1982，1995）提出Vapnik–Chervonenkis理论上的最强大的预测方法之一。给定一组训练实例，每个训练实例被标记为属于两个类别中的一个或另一个，SVM训练算法创建一个将新的实例分配给两个类别之一的模型，使其成为非概率二元线性分类器。SVM模型是将实例表示为空间中的点，这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后，将新的实例映射到同一空间，并基于它们落在间隔的哪一侧来预测所属类别。

除了进行线性分类之外，SVM还可以使用所谓的核技巧有效地进行非线性分类，将其输入隐式映射到高维特征空间中。

支持向量机涵盖有监督学习、无监督学习以及半监督学习

学习类型	功能
有监督学习	线性二分类与多分类（Linear Support Vector  Classification） 非线性二分类与多分类（Support Vector Classification, SVC） 普通连续型变量的回归（Support Vector Regression） 概率型连续变量的回归（Bayesian SVM）
无监督学习	支持向量聚类（Support Vector  Clustering，SVC） 异常值检测（One-class SVM）
半监督学习	转导支持向量机（Transductive Support Vector Machines，TSVM）

 超平面的理解：

定义：

定义：nn 维线性空间中维度为 n−1n−1 的子空间，它可以把线性空间分割为不相交的两部分。这里的 nn 必须大于 33，其子空间才能称之为超平面。

在几何中，超平面是一个空间的子空间，它是维度比所在空间小一维的空间。

如果数据空间本身是三维的，则其超平面是二维平面，而如果数据空间本身是二维的，则其超平面是一维的直线。

 

超平面方程推导：

1）平面直线方程

对于平面上的任意一条直线，它的一般方程为：ax+by+c=0

 从向量角度来看，一般方程可以写成如下形式

可以发现：直线其实就是一个常向量和另一个变化的向量的内积为定值 c。

   其中 x,y 代表直线上任意一点的坐标，所以 (x,y)T 表示从原点出发到直线上任意一点的射线构成的向量。

向量内积表示：一个向量乘以另一个向量在该向量上的正交投影

这个向量必须满足：向量 在它上面的投影都一样。这样才能保证内积为定值。

   这样的向量只有一个，那便是直线 ll 的法向量 l′l′。所以常向量就是直线的法向量。

   不同的法向量或者不同的定值 c 就意味着不同的直线方程。

2）空间平面方程

   对于空间上的任意一个平面，它的一般方程为：ax+by+cz+d=0

从向量角度来看，一般方程可以写成如下形式

和平面直线类似，上面这个方程可以理解为：一个常向量和另一个变化的向量的内积为定值 dd。

   其中常向量为这个平面的法向量，变化的向量为原点到平面上任意一点的射线构成的向量。

3）引申到超平面

   一个超平面的法向量：意味着它要垂直于该超平面内的任一个向量。

   对于 44 维空间来说，它的超平面就是一个 33 维空间，很难想象会存在一个向量，它垂直于三维空间中的任一个向量。

   我们没办法想象到三维以上的空间长啥样，但数学是纯粹逻辑上的东西，高维空间在逻辑上是存在的。

设 nn 维空间中的一个超平面的法向量为 w=(w1,w2,...,wn)Tw=(w1,w2,...,wn)T，原点到该超平面上任意一点的向量为 xT=(x1,x2,..,xn)xT=(x1,x2,..,xn)。

   由直线方程、平面方程进行推广，可知超平面方程为

点到超平面的距离推导：

1）点到平面直线的距离公式

   任一点 (x0,y0)到直线 ax+by+c=0的距离公式为:

2）点到空间平面的距离公式

   我们按照上面的思路也可以列出方程：

 所以距离 d 为

 

3）引申到超平面

   已知超平面方程为 。   类比于点到直线和平面的距离公式，有