7.1组合及其优化（LC77-M）

算法：

第一次取1 2 3 4
取1时，留下234

取2时，留下34

取3时，留下4

取4时，留下null

---

接着继续取234中的2，与1组合，得到12

取234中的3，与1组合，得到13

取234中的4，与1组合，得到14

---

接着继续取34中的3，与2组合，得到23

取34中的4，与2组合，得到24

---

接着继续取4，与3组合，得到34

---

回溯三部曲：

1.确定函数返回值和参数：返回值是void；参数：n、k（题目中都给出了），还要一个startindex，因为每次递归的时候，怎么知道从哪里开始取呢？这时候就需要一个index指引一下。

2.确定终止条件：当取到一个组合时，单层逻辑终止，比如取到12，就不会往下了；因为每个组合（12 13 14 23 24 34）都是树的叶子结点

3.单层递归逻辑：也就是单层搜索的逻辑。在这里就是for循环。

在for循环中,push入要取的数值1或2或3或4；

调用递归

回溯:撤销结果。pop

调试过程：

定义全局变量：result为二维数组，path为一维数组

数组List，用ArrayList和LinkedList都可以

class Solution {
//全局变量
    List>result = new ArrayList();
    LinkedListpath = new LinkedList();
    public List> combine(int n, int k) {
        backtracking(n,k,1);
        return result;
    }
    void backtracking (int n, int k, int startindex){
        if (path.size()==k){
            result.add(path);
            return;
        }
        for(int i=startindex;i<=n;i++){
            path.add(i);
            backtracking(n,k,i+1);//往二叉树的深处递归，所以是i+1
            path.pop();
        }
    }
}

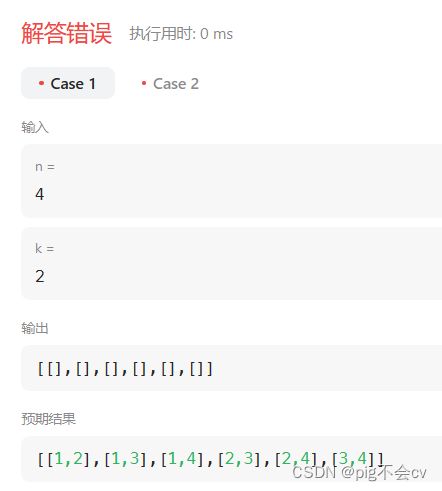
原因：输出都是空集

问题出在 `result.add(path);` 这一行以及 `path.pop();` 上

调用 `result.add(path);` 时，实际上是将 `path` 对象的引用加入了 `result` 中，而不是 `path` 对象的拷贝。随后对 `path` 对象的任何修改都会影响到 `result` 中的元素。

`path` 在递归过程中被修改了多次，但是 `result` 中存储的都是同一个 `path` 对象的引用，因此最终 `result` 中的所有元素都指向了同一个 `path` 对象。

可以在将 `path` 加入 `result` 前，先创建一个 `path` 的拷贝，然后将拷贝加入 `result`。在 Java 中，可以通过 `new LinkedList<>(path)` 来创建 `path` 的拷贝。另外，`path.pop()` 应该改为 `path.removeLast()`，因为 Java 中的 `LinkedList` 类使用 `removeLast` 来移除最后一个元素。

正确代码：

class Solution {
//全局变量
    List>result = new ArrayList();
    LinkedListpath = new LinkedList();
    public List> combine(int n, int k) {
        backtracking(n,k,1);
        return result;
    }
    void backtracking (int n, int k, int startindex){
        if (path.size()==k){
            result.add(new LinkedList<>(path));
            return;
        }
        for(int i=startindex;i<=n;i++){
            path.add(i);
            backtracking(n,k,i+1);//往二叉树的深处递归，所以是i+1
            path.removeLast();
        }
    }
}

---

剪枝优化

回溯法虽然是暴力搜索，但也有时候可以有点剪枝优化一下的。

只要改一下for循环的条件即可

来举一个例子，n = 4，k = 4的话，答案显然是[1,2,3,4]

如果像刚刚一样求，会增加很多不必要的循环：

那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。

剪枝：

缩小for循环的范围

1. 已经选择的元素个数：path.size();

2. 所需需要的元素个数为: k - path.size();

3. 列表中剩余元素 >= 所需需要的元素个数

   1. n-i >=k - path.size()

4. 在集合n中至多要从该起始位置 : i <= n - (k - path.size()) + 1，开始遍历

   1. 为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

剪枝优化后的正确代码：

class Solution {
//全局变量
    List>result = new ArrayList();
    LinkedListpath = new LinkedList();
    public List> combine(int n, int k) {
        backtracking(n,k,1);
        return result;
    }
    void backtracking (int n, int k, int startindex){
        if (path.size()==k){
            result.add(new LinkedList<>(path));
            return;
        }
        for(int i=startindex; i <= n - (k - path.size())+1;i++){
            path.add(i);
            backtracking(n,k,i+1);//往二叉树的深处递归，所以是i+1
            path.removeLast();
        }
    }
}