读书笔记 | 自动驾驶中的雷达信号处理(第5章 雷达目标检测 )
本文编辑:调皮哥的小助理
5.1 介绍
目标检测的目的通常是将真实的目标回波信号从噪声和杂波中区分出来,本章讨论了雷达探测的主要概念和方法,其中包含CFAR算法等内容。
5.2 目标类型(Sterling 1型~Sterling 4型)
目标雷达截面(RCS)统计特性的可用性可以显著提高目标检测算法的性能,为此,Swerling引入了Swerling模型从不同自由度卡方分布来描述物体RCS的统计特性,从I到V有5种不同的Swerling模型,总结如下。
5.2.1 Swerling I
单次扫描中的目标反射具有恒定的 RCS 幅度 ,但它根据具有两个自由度的卡方概率密度函数 (PDF) 随扫描而变化。 PDF由以下表达式给出:
f ( σ ) = 1 σ avg e − σ σ avg , σ ≥ 0 f(\sigma)=\frac{1}{\sigma_{\text {avg }}} \mathrm{e}^{-\frac{\sigma}{\sigma_{\text {avg }}}}, \quad \sigma \geq 0 f(σ)=σavg 1e−σavg σ,σ≥0(5.1)
其中, σ a v g \sigma_{a v g} σavg 为RCS的均值。
5.2.2 Swerling II
RCS的PDF与公式(4.1)相同,但与脉冲间是相互独立的,而不是与扫描间的相互独立。
5.2.3 Swerling III
RCS和Swerling I有相同的描述,但不同的是Swerling III有四个自由度,PDF由以下表达式给出。
f ( σ ) = 4 σ σ a v g 2 e − 2 σ σ a v g , σ ≥ 0 f(\sigma)=\frac{4 \sigma}{\sigma_{\mathrm{avg}}^2} \mathrm{e}^{-\frac{2 \sigma}{\sigma_{\mathrm{avg}}}}, \quad \sigma \geq 0 f(σ)=σavg24σe−σavg2σ,σ≥0(5.2)
5.2.4 Swerling IV
RCS根据公式.(5.2)在不同脉冲之间变化,而不是在不同扫描之间变化。
5.2.5 Swerling V (Swerling 0)
RCS是常数,这意味着具有无限的自由度。
Swerling 模型在理论研究以及在研究可预测 RCS 行为的单一目标的情况下也很重要。 然而,在杂波中存在多个动态目标的情况下,使用模型确定检测阈值可能具有挑战性 。Swerling模型1至4的总结:

Swerling 模型可以嵌入到目标检测概率中,如下所示。 如果阈值检测器的输入信号由嵌入方差 ξ 2 \xi^2 ξ2 的高斯噪声中的幅度为 A A A 的信号分量组成,用 r ( t ) r(t) r(t) 表示,则 r ( t ) r(t) r(t) 的概率密度函数可以表示为:
f ( r ( t ) ) = r ( t ) ξ 2 I 0 ( r A ξ 2 ) e − r ( t ) 2 + A 2 2 ξ 2 f(r(t))=\frac{r(t)}{\xi^2} I_0\left(\frac{r A}{\xi^2}\right) \mathrm{e}^{-\frac{r(t)^2+A^2}{2 \xi^2}} f(r(t))=ξ2r(t)I0(ξ2rA)e−2ξ2r(t)2+A2(5.3)
为第一类零阶修正贝塞尔函数。上式定义了一个Rician概率密度函数。如果只是噪声,则:
f ( r ( t ) ) = r ( t ) ξ 2 I 0 ( r ( t ) A ξ 2 ) e − r ( t ) 2 2 ξ 2 f(r(t))=\frac{r(t)}{\xi^2} I_0\left(\frac{r(t) A}{\xi^2}\right) \mathrm{e}^{-\frac{r(t)^2}{2 \xi^2}} f(r(t))=ξ2r(t)I0(ξ2r(t)A)e−2ξ2r(t)2(5.4)
这是瑞利分布函数,当信噪比较大时,瑞利近似于高斯分布。
f ( r ( t ) ) ≈ 1 2 ξ 2 e − ( r ( t ) − A ) 2 2 ξ 2 f(r(t)) \approx \frac{1}{\sqrt{2 \xi^2}} \mathrm{e}^{-\frac{(r(t)-A)^2}{2 \xi^2}} f(r(t))≈2ξ21e−2ξ2(r(t)−A)2(5.5)
5.2.6 虚警概率
对于给定的检测阈值 P t h r P_{t h r} Pthr ,误报概率 是由下面公式表示:
P f a = ∫ P t h r ∞ r ( t ) ξ 2 e − ( r ( t ) ) 2 2 ξ 2 d ( r ( t ) ) = e − ( P t h r ) 2 2 ξ 2 P_{\mathrm{fa}}=\int_{P_{\mathrm{thr}}}^{\infty} \frac{r(t)}{\xi^2} \mathrm{e}^{-\frac{(r(t))^2}{2 \xi^2} \mathrm{~d}(r(t))}=\mathrm{e}^{-\frac{\left(P_{\mathrm{thr}}\right)^2}{2 \xi^2}} Pfa=∫Pthr∞ξ2r(t)e−2ξ2(r(t))2 d(r(t))=e−2ξ2(Pthr)2(5.6)
由上式,阈值可以用虚警概率表示为:
P t h r = 2 ξ 2 ln ( 1 P f a ) P_{\mathrm{thr}}=\sqrt{2 \xi^2 \ln \left(\frac{1}{P_{\mathrm{fa}}}\right)} Pthr=2ξ2ln(Pfa1)(5.7)
5.2.7 检测概率
由 r ( t ) r(t) r(t) 的PDF,我们可以定义检测概率为:
P D = ∫ P i h r ∞ r ( t ) ξ 2 I 0 ( r A ξ 2 ) e − r ( t ) 2 + A 2 2 ξ 2 d ( r ( t ) ) P_D=\int_{P_{\mathrm{ihr}}}^{\infty} \frac{r(t)}{\xi^2} I_0\left(\frac{r A}{\xi^2}\right) \mathrm{e}^{-\frac{r(t)^2+A^2}{2 \xi^2}} \mathrm{~d}(r(t)) PD=∫Pihr∞ξ2r(t)I0(ξ2rA)e−2ξ2r(t)2+A2 d(r(t))(5.8)
P f a P_{f a} Pfa和 P D P_D PD 的许多近似值是可能的,并且可以从表格中获得实现给定 P f a P_{f a} Pfa和 P D P_D PD 所需的 SNR 。目标检测的联合概率密度函数 f ( x , σ ) f(x, \sigma) f(x,σ)可以定义为:
f ( x , σ ) = f ( x / σ ) f ( σ ) f(x, \sigma)=f(x / \sigma) f(\sigma) f(x,σ)=f(x/σ)f(σ)(5.9)
检测概率 f ( x ) f(x) f(x) 为:
f ( x ) = ∫ f ( x , σ ) d ( σ ) = ∫ f ( x / σ ) f ( σ ) d ( σ ) f(x)=\int f(x, \sigma) \mathrm{d}(\sigma)=\int f(x / \sigma) f(\sigma) \mathrm{d}(\sigma) f(x)=∫f(x,σ)d(σ)=∫f(x/σ)f(σ)d(σ)(5.10)
其中,条件概率密度函数 f ( x , σ ) f(x, \sigma) f(x,σ)为:
f ( x / σ ) = ( 2 x ξ 2 M σ 2 ) M − 1 2 e ( − x − 1 2 ∗ M σ 2 ξ 2 ) I M − 1 ( 2 M x σ 2 ξ 2 ) f(x / \sigma)=\left(\frac{2 x \xi^2}{M \sigma^2}\right)^{\frac{M-1}{2}} \mathrm{e}^{\left(-x-\frac{1}{2} * \frac{M \sigma^2}{\xi^2}\right)} I_{M-1}\left(\sqrt{\frac{2 M x \sigma^2}{\xi^2}}\right) f(x/σ)=(Mσ22xξ2)2M−1e(−x−21∗ξ2Mσ2)IM−1(ξ22Mxσ2)(5.11)
M M M 为脉冲积累个数,对 f ( x ) f(x) f(x) 积分得到不完全函数。
从汽车的角度来看,可以从对地面车辆的调查结果中获得对起伏目标模型的了解。地面车辆由中描述的大型货车、大型卡车、中型轿车和中型卡车组成, Swerling I 地面车辆的目标行为被证明是所有数据集分布和参数变化的最普遍情况,尽管角度变化是有限的。
此外,Swerling III 目标行为可应用于大约 90% 的采样数据,但对雷达分辨率的依赖性被确定为相关因素。总之,Swerling 模型的选择成为考虑信噪比 (SNR)、检测概率和误报概率性能要求的设计决策,尽管推荐的保守方法是使用 Swerling I 目标模型。最近的一些研究还表明,与 Swerling 模型中使用的 Gamma 分布不同,Weibull 分布最适合测量来自各种个人车辆类别的雷达反射 。
5.3峰值检测
在存在噪声和杂波的情况下,为了从接收到的反射信号中选择有效的目标,需要进行峰值检测。
频谱通常由多个峰组成,如图1所示。对于汽车应用来说,由于接收到的反射信号由路边障碍物和地面反射组成,因此峰值检测变得更加困难。不同的策略可以获得不同程度的效果来完成峰值检测任务,大多数情况下,峰值检测是使用的是距离-多普勒谱实现。
在接下来的小节中,我们将简要介绍峰值检测算法背后的理论背景。
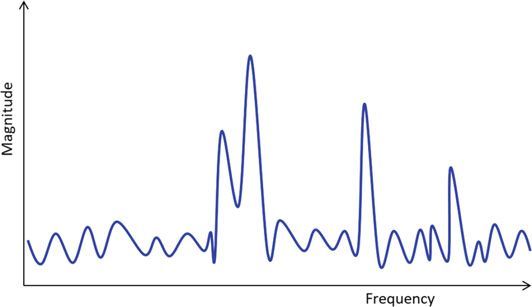
(图1 FFT后得到的典型距离谱图,峰值检测任务是提取目标峰值,并避免提取到噪声电平 。)
5.3.1 确定阈值
阈值检测器(内曼-皮尔森检测器)是最简单的用于峰值检测的方法。在这种情况下,设置了一个预先确定的阈值,则超过该阈值的目标被认为是有效的。若接收信号由目标回波信号 s ( t ) s(t) s(t) 和噪声 n ( t ) n(t) n(t) 组成,阈值设为 P t h r P_{t h r} Pthr ,则检测规则可表示为:
s ( t ) + n ( t ) ≥ P t h r , s(t)+n(t) \geq P_{t h r}, \quad s(t)+n(t)≥Pthr, TrueDetection
n ( t ) ≥ P thr , n(t) \geq P_{\text {thr }}, \quad n(t)≥Pthr , False Alarm
其含义是在实际情况中只有噪声存在的情况下,当存在目标被确定时,就出现了虚警。对于相同反射模型的非起伏目标,上述表达式是正确的,但当雷达视场中存在不同目标的混合时,上述表达式失效。此外,目标反射特性还受到距离、角度、尺寸等目标形状因素的影响。因此,将需要多个单元阈值来描述这类场景,为此,自适应检测阈值长期以来一直是研究的课题。
5.3.2 多单元的阈值
多单元阈值技术对于处理实际中出现的计算DFT功率扩展到相邻距离或多普勒单元的情况是必要的。在这种情况下,希望从这样一组 单元中仅检测一个峰值,该策略只是比较连续的 单元并在所考虑的单元 任一侧的梯度发生变化时做出检测决定。以距离仓(距离单元、距离门)为例,这里的假设是,如果目标被至少一个距离仓分离,这种方法的缺点是有些目标在峰值附近表现出起伏行为,当实际只存在单个目标时,会导致多个目标的检测。此外,在不对噪声施加第二阈值的情况下,噪声有可能导致过度的虚警。
5.3.3 恒虚警检测(CFAR)
为了解决与固定阈值和多单元阈值相关的问题,我们已经应用了CFAR方法,并取得了一定的成功。应该记住,这种方法不是没有代价(计算成本)的。在汽车雷达应用中,除了雷达尺寸之外,计算成本的增加也是一个重要问题。
CFAR检测算法的要求每次处理都会增加计算速度和设备内存,因此必须在性能和成本之间进行权衡。在本节中,我们简要地概述了一些重要的CFAR算法。
虚警是指从雷达回波中误检目标。传统的计算是在所有距离单元中只有噪声存在时,通过估计目标检测次数来计算。
保持虚警常数是可取的,因为检测算法对接收雷达回波中几乎总是存在的噪声和杂波非常敏感。因此,所有雷达探测方案的总体目标是确保虚警不随意波动。在检测过程中,每个单元使用一个阈值来评估目标的存在与否。有利于在保持恒定虚警率的同时,能够同时检测出高真实和低真实目标。这就要求采用自适应阈值法,现代雷达大多采用这种方法,基本CFAR方法中最常用的形式如平均单元CFAR ( CA- CFAR )、单元平均最大CFAR ( CAGO- CFAR )、单元平均最小CFAR ( CAGO- CFAR )。
5.3.4 CFAR
CFAR原则可追溯到20世纪60年代末。解决虚警问题的方法包括执行恒虚警率( CFAR )方案,改变检测阈值作为感知环境的函数。虽然CFAR模型存在着大量的类型,但它们通常都是围绕着‘背景平均器’( 有时被称为单元平均化 CFAR )展开的。简化框图如图2所示。该模型估计距离单元两侧雷达距离单元的干扰(噪声或杂波)水平,并利用这个估计来决定中心感兴趣的单元中是否存在目标。该过程在范围内逐步取出一个细胞,重复进行,直到所有范围细胞都被考察完毕。
模型背后的基本思想是,当噪声存在时,感兴趣单元周围的单元将包含对被测单元噪声的良好估计;即假设噪声或干扰在空间上暂时是均匀的。理论上,模型会产生一个恒定的虚警率,它与噪声或杂波水平无关,只要噪声在模型所研究的所有距离内都为瑞利分布。
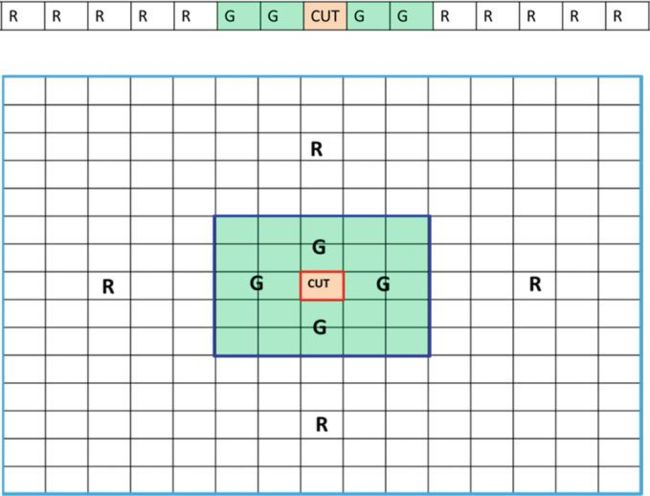
(图2用于一维 CFAR和二维 CFAR的单元示例。CUT是被测单元。标记为G区域的单元是保护单元,标记为R区域的单元是参考单元。)
Cell-Averaging CFAR (CA-CFAR)
在这种方法中,如图3所示,阈值是通过取待测单元格( CUT )周围单元格的平均功率来计算的,而不是取单一的固定值。CUT是待确定存在或不存在或目标的单元。为了确保CUT不影响阈值计算,立即将CUT周围的单元格排除在计算之外,这些单元被称为保护单元。对于一维CFAR,保护单元位于CUT左右,而对于二维CFAR,保护单元围绕CUT形成环状。在CUT中判断一个目标是否存在:功率大于所有保护单元的功率,也大于计算的平均功率电平。
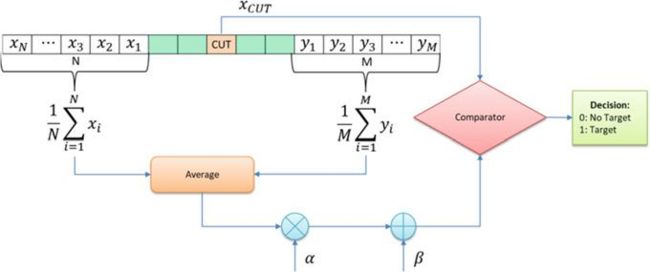
(图3 CFAR检测原理。用乘法α和偏置β来调整平均值)
Cell-Averaging Greatest-Of CFAR (CAGO-CFAR)
这是CA-CFAR的一种变化,在一维情况下,分别对左侧和右侧单元进行平均。然后,阈值就是两个结果的最大值。该方法如图4所示。
用于阈值计算的平均值如下:
T aver = MAX ( 1 N ∑ i = 1 N x i , 1 M ∑ i = 1 M y i ) T_{\text {aver }}=\operatorname{MAX}\left(\frac{1}{N} \sum_{i=1}^N x_i, \frac{1}{M} \sum_{i=1}^M y_i\right) Taver =MAX(N1∑i=1Nxi,M1∑i=1Myi)(5.12)
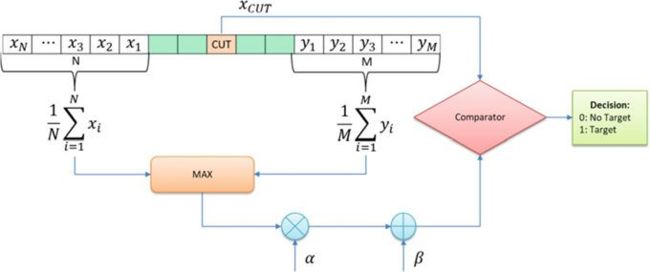
(图4 CAGO-CFAR)
Cell-Averaging Ordered Statistic CFAR (CAOS-CFAR)
这与CAGO- CFAR类似,只是计算了最小值而不是最大值。CASO-CFAR有增加对低功耗弱小目标的探测的效果,但同时有增加误检的风险。图5显示了工作原理。阈值计算所用的平均值如下:
T aver = MIN ( 1 N ∑ i = 1 N x i , 1 M ∑ i = 1 M y i ) T_{\text {aver }}=\operatorname{MIN}\left(\frac{1}{N} \sum_{i=1}^N x_i, \frac{1}{M} \sum_{i=1}^M y_i\right) Taver =MIN(N1∑i=1Nxi,M1∑i=1Myi)(5.13)

(图5 CASO-CFAR)
Cell-Averaging Ordered Statistic CFAR (CAOS-CFAR)
CAOS-CFAR 不是像在其他 CFAR 变体中那样获取平均值,而是计算参考单元的顺序统计量 。 顺序统计中的排名是预先确定的,可以通过对所有值取排名来选择阈值平均值,或者在分别考虑左侧和右侧时通过CAGO-CFAR/CASO-CFAR来选择阈值平均值。 CAOS-CFAR 对弱小目标实现了性能改进, 然而所需的单元分类大大增加了计算复杂性,使其难以在汽车应用中实现。 该方法的模型图如图 6 所示。
对于任何一组值 { a 1 , a 2 , … , a n } \{a 1, a 2, \ldots, a n\} {a1,a2,…,an} ,顺序统计运算首先将值排序为序列 { a ( 1 ) , a ( 2 ) , … , a ( n ) } \{a(1), a(2), \ldots, a(n)\} {a(1),a(2),…,a(n)} 从中选择第 k k k 个值。
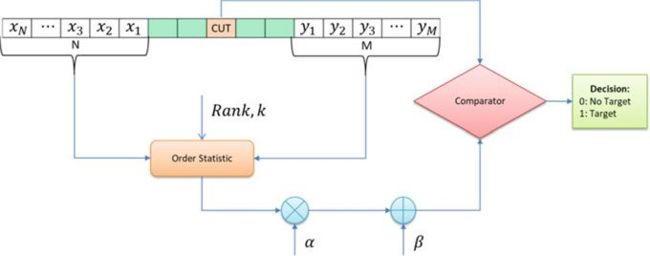
(图6 CAOS-CFAR)
Cell-Averaging Statistic Hofele (CASH-CFAR)
图7所示的单元平均统计量 Hofele CFAR (CASH-CFAR) 基于与每个距离单元相关的一系列求和单元以及特定的最大-最小检测器 。 它利用一系列子寄存器来执行求和,从中选择最小值,然后将其视为 CA-CFAR 的平均值, 与 CAOS-CFAR 相比,CASH-CFAR 算法的优点是减少了计算量,同时具有相似的性能。
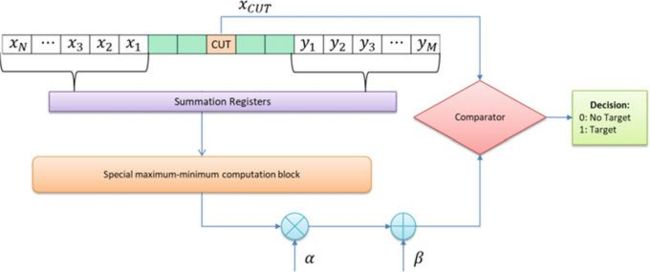
(图7 CASH-CFAR)
Maximum–Minimum Statistic CFAR (MAMIS-CFAR)
最大-最小统计CFAR(MAMIS-CFAR)建立在与CASH-CFAR相同的原理上,不同之处在于使用特殊的最大-最小检测器而不是CASH-CFAR算法的求和块。 尽管文献中已经提出了多种其他 CFAR 算法,例如 MAMIS 和 CASH,但 CA-CFAR、CAGO-CFAR、CASO-CFAR 和 CAOS-CFAR 仍然是最流行和最容易理解的方法。
如前所述,计算复杂性和其他考虑因素可能会阻止使用这些更稳健的算法来支持简单的阈值技术,尤其是在汽车应用中。 尽管如此,随着降低硬件成本和高速处理器可用性的前景越来越大,转向高性能算法是不可避免的。
关于CFAR的更多内容,请各位读者阅读下面这本书(电子版见链接):
调皮连续波:干货 | 再次解读雷达信号处理中的快速二维CFAR(2D-CFAR、十字CFAR)检测算法
