【数据结构入门精讲 | 第十六篇】并查集知识点及考研408、企业面试练习

上一篇中我们进行了散列表的相关练习，在这一篇中我们要学习的是并查集。

在许多实际应用场景中，我们需要对元素进行分组，并且在这些分组中进行查询和修改操作。比如，在图论中，我们需要将节点按照连通性进行分组，以便进行最小生成树、最短路径等算法；在计算机视觉中，我们需要将像素进行分组，以便进行图像分割和对象识别等任务。而并查集正是为了解决这些问题而被提出来的一种数据结构。

概念

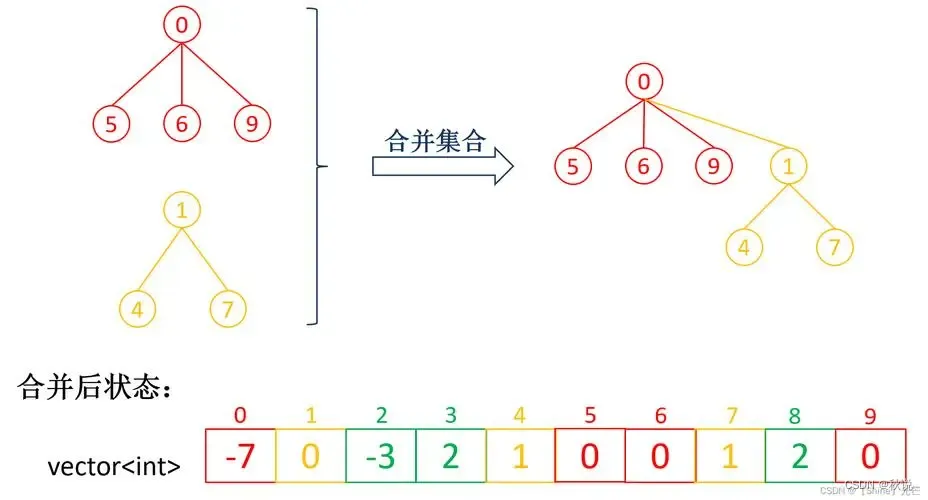
并查集（Disjoint Set）是一种用于处理元素分组的数据结构，通常用于解决一些与等价关系有关的问题，比如连通性的判断、最小生成树算法中的边的合并等。

并查集中的每个元素都属于一个集合，每个集合都有一个代表元素（也称为根节点），代表元素可以用来表示整个集合。并查集支持三个基本操作：

1.MakeSet(x)：创建一个只包含元素 x 的新集合；
2.Find(x)：返回元素 x 所属的集合的代表元素；
3.Union(x, y)：将元素 x 和 y 所属的集合合并成一个新集合。

其中，Find 操作可以使用路径压缩（Path Compression）和按秩合并（Union by Rank）优化，以提高查询效率。

并查集的应用非常广泛，比如在图论算法中求解连通性、求解最小生成树等问题时都会用到。

伪代码

// 初始化并查集，每个元素单独成集合
function MakeSet(x)
    x.parent = x
    x.rank = 0

// 查找元素所属的集合（根节点），并进行路径压缩
function Find(x)
    if x.parent != x
        x.parent = Find(x.parent) // 路径压缩：将x的父节点设为根节点
    return x.parent

// 合并两个集合，按秩合并
function Union(x, y)
    xRoot = Find(x)
    yRoot = Find(y)
    if xRoot == yRoot
        return // 已经在同一个集合中，无需合并
    if xRoot.rank < yRoot.rank
        xRoot.parent = yRoot
    else if xRoot.rank > yRoot.rank
        yRoot.parent = xRoot
    else
        yRoot.parent = xRoot
        xRoot.rank = xRoot.rank + 1

接下来，让我们进行并查集的相关练习。

选择题

1.

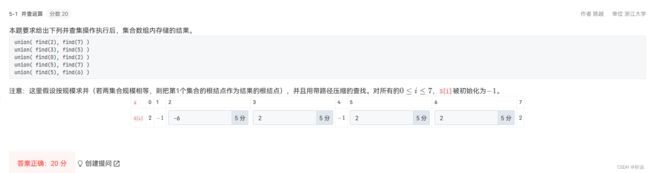
选B

2.

解析：
1  -4   1  1  -3  4  4  8  -2
0   1   2  3   4  5  6  7   8


1对应-4，则1是根节点且有4个子孙
又因为0、2、3都对应1
所以
      1
   0 2 3 null
   
   
4对应-3，则4是根节点且有3个子孙
又因为5、6都对应4
所以
    4
  5  6 null
  
  
8对应-2，则8是根节点且有2个子孙
又因为7对应8
所以
    8
  7 null
  
将6与8所在的集合合并，且小集合合并到大集合
则
    4
  5  6 8
      7 null
所以树根是4，对应的编号是-5（-表示树根，5表示4的子孙个数）

3.

可以画出来对应的树
然后把小树连到大树上
接着从1到7遍历
如果有父节点，给出父节点的值
如果它本身是根节点，则给出负号和子孙个数

填空题

编程题

7-1 朋友圈

某学校有N个学生，形成M个俱乐部。每个俱乐部里的学生有着一定相似的兴趣爱好，形成一个朋友圈。一个学生可以同时属于若干个不同的俱乐部。根据“我的朋友的朋友也是我的朋友”这个推论可以得出，如果A和B是朋友，且B和C是朋友，则A和C也是朋友。请编写程序计算最大朋友圈中有多少人。

输入格式:

输入的第一行包含两个正整数N（≤30000）和M（≤1000），分别代表学校的学生总数和俱乐部的个数。后面的M行每行按以下格式给出1个俱乐部的信息，其中学生从1~N编号：

第i个俱乐部的人数Mi（空格）学生1（空格）学生2 … 学生Mi

输出格式:

输出给出一个整数，表示在最大朋友圈中有多少人。

输入样例:

7 4
3 1 2 3
2 1 4
3 5 6 7
1 6

输出样例:

4

#include 

int a[30001];  // 定义数组a，用于存储并查集的父节点信息
int search(int b){  // 查找元素所属的集合（根节点）
	if(a[b]<0){  // 如果a[b]小于0，说明b是根节点
		return b;  // 返回b作为集合的代表元素
	}else{
		return search(a[b]);  // 否则递归查找父节点，直到找到根节点
	}
}

void function(int m,int n){  // 合并两个集合
	int x,y;
	x=search(m);  // 查找m所属的集合（根节点）
	y=search(n);  // 查找n所属的集合（根节点）
	if(x!=y){  // 如果m和n不在同一个集合中
		a[x]+=a[y];  // 将集合y的大小加到集合x上
		a[y]=x;  // 将集合y的父节点指向集合x
	}
}

int main(){
	int m,n;
	scanf("%d %d",&n,&m);  // 输入学生数量n和关系数量m
	int i;
	for(i=0;i<=n;i++){  // 初始化并查集，每个元素单独成集合
		a[i]=-1;  // 初始时每个元素的父节点为自身，且集合大小为1
	}
	int stu,j,num,num1;
	for(i=0;i<m;i++){  // 处理每组关系
		scanf("%d",&stu);  // 输入每组关系中学生的数量
		for(j=0;j<stu;j++){  // 输入每组关系中的学生编号
			scanf("%d",&num);
			if(j==0){
				num1=num;  // 记录第一个学生的编号
			}else{
				function(num1,num);  // 合并这组关系中的学生
			}
		}
	}
	int min;
	min=a[1];
	for(i=2;i<n;i++){  // 找到集合中最小的负数，作为集合大小的相反数
		if(min>a[i]){
			min=a[i];
		}
	}
	printf("%d",-min);  // 输出最少需要分成的组数
}

R7-1 笛卡尔树

笛卡尔树是一种特殊的二叉树，其结点包含两个关键字K1和K2。首先笛卡尔树是关于K1的二叉搜索树，即结点左子树的所有K1值都比该结点的K1值小，右子树则大。其次所有结点的K2关键字满足优先队列（不妨设为最小堆）的顺序要求，即该结点的K2值比其子树中所有结点的K2值小。给定一棵二叉树，请判断该树是否笛卡尔树。

输入格式:

输入首先给出正整数N（≤1000），为树中结点的个数。随后N行，每行给出一个结点的信息，包括：结点的K1值、K2值、左孩子结点编号、右孩子结点编号。设结点从0~(N-1)顺序编号。若某结点不存在孩子结点，则该位置给出−1。

输出格式:

输出YES如果该树是一棵笛卡尔树；否则输出NO。

输入样例1:

6
8 27 5 1
9 40 -1 -1
10 20 0 3
12 21 -1 4
15 22 -1 -1
5 35 -1 -1

输出样例1:

YES

输入样例2:

6
8 27 5 1
9 40 -1 -1
10 20 0 3
12 11 -1 4
15 22 -1 -1
50 35 -1 -1

输出样例2:

NO

#include
using namespace std;
struct Node{
    int k1;
    int k2;
    int left_c;
    int right_c;
}a[1200];  // 定义结构体Node，表示二叉树的每个节点
int root,flag=1;  // 定义变量root表示根节点，flag表示是否符合条件
int b[1200];  // 定义数组b，用于标记每个节点是否有左右孩子
int zhongxu[1200],cnt=0;  // 定义数组zhongxu，存储中序遍历序列，cnt为元素数量

void midorder(int root){  // 中序遍历二叉树
    if(root!=-1){  // 如果根节点不为空
        midorder(a[root].left_c);  // 遍历左子树
        zhongxu[cnt]=a[root].k1;  // 将当前节点的值存入中序遍历序列中
        cnt++;  // 记录元素数量
        midorder(a[root].right_c);  // 遍历右子树
    }
}

void judgeheap(int root){  // 判断是否为堆
    int left,right;
    if(a[root].left_c!=-1){  // 如果左孩子存在
        left=a[root].left_c;
        if(a[left].k2<a[root].k2){  // 如果左孩子的值小于根节点的值
            flag=0;  // 不符合堆的条件
            return ;
        }
        judgeheap(left);  // 递归遍历左子树
    }
    if(a[root].right_c!=-1){  // 如果右孩子存在
        right=a[root].right_c;
        if(a[right].k2<a[root].k2){  // 如果右孩子的值小于根节点的值
            flag=0;  // 不符合堆的条件
            return ;
        }
        judgeheap(right);  // 递归遍历右子树
    }
}

int main()
{
    int n;
    cin>>n;  // 输入节点数量n
    int i,K1,K2,Left,Right;
    memset(b,0,sizeof(b));  // 初始化数组b，全部置为0
    for(i=0;i<n;i++)  // 处理每个节点的信息
    {
        scanf("%d %d %d %d",&K1,&K2,&Left,&Right);  // 输入节点的值、权值、左右孩子的编号
        a[i].k1=K1;  // 将节点的值存入结构体
        a[i].k2=K2;  // 将节点的权值存入结构体
        a[i].left_c=Left;  // 将左孩子编号存入结构体
        a[i].right_c=Right;  // 将右孩子编号存入结构体
        if(Left!=-1)  // 如果左孩子存在
            b[Left]=1;  // 标记左孩子编号为1
        if(Right!=-1)  // 如果右孩子存在
            b[Right]=1;  // 标记右孩子编号为1  
    }  
    for(i=0;i<n;i++){  // 找到根节点
        if(b[i]==0){  // 如果节点没有左右孩子，说明其为根节点
            root=i;
            break;
        }
    }
    midorder(root);  // 中序遍历二叉树，得到中序遍历序列
    for(i=1;i<cnt;i++){  // 判断是否为完全二叉树
        if(zhongxu[i]<=zhongxu[i-1]){  // 如果中序遍历序列不是单调递增的
            flag=0;  // 不符合完全二叉树的条件
            break;
        }
    }
    judgeheap(root);  // 判断是否为堆
    if(flag)  // 如果符合条件
        printf("YES\n");  // 输出YES
    else
       printf("NO\n");  // 输出NO
    return 0;
}

R7-2 部落

在一个社区里，每个人都有自己的小圈子，还可能同时属于很多不同的朋友圈。我们认为朋友的朋友都算在一个部落里，于是要请你统计一下，在一个给定社区中，到底有多少个互不相交的部落？并且检查任意两个人是否属于同一个部落。

输入格式：

输入在第一行给出一个正整数N（≤104），是已知小圈子的个数。随后N行，每行按下列格式给出一个小圈子里的人：

K P[1] P[2] ⋯ P[K]

其中K是小圈子里的人数，P[i]（i=1,⋯,K）是小圈子里每个人的编号。这里所有人的编号从1开始连续编号，最大编号不会超过104。

之后一行给出一个非负整数Q（≤104），是查询次数。随后Q行，每行给出一对被查询的人的编号。

输出格式：

首先在一行中输出这个社区的总人数、以及互不相交的部落的个数。随后对每一次查询，如果他们属于同一个部落，则在一行中输出Y，否则输出N。

输入样例：

4
3 10 1 2
2 3 4
4 1 5 7 8
3 9 6 4
2
10 5
3 7

输出样例：

10 2
Y
N

#include
#include
#include
using namespace std;
int pre[10010];  // 定义数组pre，用于存储每个元素的祖先

int find(int x){  // 查找操作，返回x的祖先
    if(pre[x]==x) return x;
    return pre[x]=find(pre[x]);
} 

void unite(int x,int y){  // 合并操作，将x所在集合和y所在集合合并
    x=find(x);
    y=find(y);
    if(x!=y)
        pre[x]=y;
}

int main(){
    int n,x,y,m,a;
    for(int i=1;i<=10000;i++) pre[i]=i;  // 初始化每个元素的祖先为自身
    set<int>s,ss;  // 定义两个set容器s和ss，分别用于存储所有元素和合并后的元素
    cin>>n;  // 输入集合数量n
    while(n--){  // 处理每个集合
        cin>>m;  // 输入集合中元素数量m
        cin>>x;  // 输入第一个元素的值
        s.insert(x);  // 将第一个元素插入到集合s中
        for(int i=1;i<m;i++){  // 处理集合中的其他元素
            cin>>y;  // 输入元素的值
            s.insert(y);  // 将元素插入到集合s中
            unite(x,y);  // 将元素x和元素y所在的集合合并
        }
    }
    set<int>::iterator it;  // 定义迭代器it，用于遍历集合s中的元素
    for(it=s.begin();it!=s.end();it++)  // 遍历集合s中的元素
        ss.insert(find(*it));  // 将每个元素的祖先插入到集合ss中
    printf("%d %d\n",s.size(),ss.size());  // 输出集合s的大小和集合ss的大小
    cin>>a;  // 输入查询次数a
    while(a--){  // 处理每次查询
        cin>>x>>y;  // 输入要查询的两个元素
        if(find(x)==find(y))  // 如果两个元素的祖先相同
            puts("Y");  // 输出Y
        else
            puts("N");  // 输出N
    }
    return 0;
}

R7-3 秀恩爱分得快

古人云：秀恩爱，分得快。

互联网上每天都有大量人发布大量照片，我们通过分析这些照片，可以分析人与人之间的亲密度。如果一张照片上出现了 K 个人，这些人两两间的亲密度就被定义为 1/K。任意两个人如果同时出现在若干张照片里，他们之间的亲密度就是所有这些同框照片对应的亲密度之和。下面给定一批照片，请你分析一对给定的情侣，看看他们分别有没有亲密度更高的异性朋友？

输入格式：

输入在第一行给出 2 个正整数：N（不超过1000，为总人数——简单起见，我们把所有人从 0 到 N-1 编号。为了区分性别，我们用编号前的负号表示女性）和 M（不超过1000，为照片总数）。随后 M 行，每行给出一张照片的信息，格式如下：

K P[1] ... P[K]

其中 K（≤ 500）是该照片中出现的人数，P[1] ~ P[K] 就是这些人的编号。最后一行给出一对异性情侣的编号 A 和 B。同行数字以空格分隔。题目保证每个人只有一个性别，并且不会在同一张照片里出现多次。

输出格式：

首先输出 A PA，其中 PA 是与 A 最亲密的异性。如果 PA 不唯一，则按他们编号的绝对值递增输出；然后类似地输出 B PB。但如果 A 和 B 正是彼此亲密度最高的一对，则只输出他们的编号，无论是否还有其他人并列。

输入样例 1：

10 4
4 -1 2 -3 4
4 2 -3 -5 -6
3 2 4 -5
3 -6 0 2
-3 2

输出样例 1：

-3 2
2 -5
2 -6

输入样例 2：

4 4
4 -1 2 -3 0
2 0 -3
2 2 -3
2 -1 2 
-3 2

输出样例 2：

-3 2

#include
using namespace std;
#define ll long long
#define rep(i,a,b) for(int i=(a);i<(b);++i)
#define maxn 4019
int n,m,k[maxn],A,B,sexa,sexb; //人数，图片数，每张图片的人数数组，两个人的编号，两个人的性别
int fu[maxn],pic[maxn][maxn],pwa[maxn],pwb[maxn]; //人的性别数组，图片中的人物编号数组，用于计算亲密度的临时数组
double pa[maxn],pb[maxn]; //与A、B的亲密度数组
vector<int>ans1,ans2; //存储亲密度最高的人的编号
 
struct gg
{
    int id; //人的编号
    double v; //与A或B的亲密程度
} p1[maxn],p2[maxn]; //用于排序的临时结构体数组
 
//读取带负号的字符串并转换为整数
int read(char*str,int ans,int *fu_)
{
    if(str[0]=='-')
    {
        int len=strlen(str);
        rep(t,1,len)
        ans=ans*10+str[t]-'0';
        *fu_=-1; //标记为负数
    }
    else
    {
        int len=strlen(str);
        rep(t,0,len)
        ans=ans*10+str[t]-'0';
        *fu_=0; //标记为非负数
    }
    return ans;
}
 
//根据性别计算与A或B的亲密度
void getpwith_(int index,int row)
{
    memset(pwa,0,sizeof(pwa)); //清空临时数组
    int sex=index==1?sexa:sexb; //根据index确定性别
 
    rep(j,0,k[row])
    {
        int peo=pic[row][j];
        if(fu[peo]!=sex) //与A或B的性别不同的人，亲密度加1
        {
            if(index)
                pwa[peo]=1;
            else
                pwb[peo]=1;
        }
    }
}
 
//比较函数，用于排序
int cmp(gg x,gg y)
{
    if(x.v!=y.v)
        return x.v>y.v;
    return x.id<y.id;
}
 
int main()
{
    scanf("%d%d",&n,&m); //读取人数和图片数
    rep(i,0,m)
    {
        scanf("%d",&k[i]); //读取每张图片中的人数
        char str[maxn];
 
        //(1)读取pic[][]:存储出现过的每张图片里的具体人物编号和性别
        rep(j,0,k[i])
        {
            scanf("%s",str);
            //读取多位数
            int fu_;
            pic[i][j]=read(str,pic[i][j],&fu_); //读取人物编号并标记性别
            fu[pic[i][j]]=fu_; //记录人的性别
        }
    }
    char AA[maxn],BB[maxn];
    scanf("%s%s",AA,BB); //读取两个人的编号字符串
    A=read(AA,0,&sexa); //将字符串转换为整数，并记录性别
    B=read(BB,0,&sexb);
 
    /*当某个人和谁的好感度都是0，这时候只输出所有异性*/
    rep(i,0,n){
        if(fu[i]==sexa)
            pa[i]+=-1; //当与A的亲密度为0时，将其置为-1
        if(fu[i]==sexb)
            pb[i]+=-1; //当与B的亲密度为0时，将其置为-1
    }
 
    //(2)计算flaga,flagb(局部变量):标记计算m张图片里是否出现过A,B
    rep(i,0,m)
    {
        int flaga=0;
        int flagb=0;
        rep(j,0,k[i])
        {
            if(pic[i][j]==A)
                flaga=1; //标记A在当前图片中出现过
            if(pic[i][j]==B)
                flagb=1; //标记B在当前图片中出现过
        }
 
        if(flaga) //计算A在局部和每个人同框的次数
        {
            getpwith_(1,i); //计算与A的亲密度
            rep(j,0,k[i])
            pa[pic[i][j]]+=pwa[pic[i][j]]/double(k[i]); //累加亲密度
        }
        if(flagb)//计算B在局部和每个人同框的次数
        {
            getpwith_(0,i); //计算与B的亲密度
            rep(j,0,k[i])
            pb[pic[i][j]]+=pwb[pic[i][j]]/double(k[i]); //累加亲密度
        }
    }
 
    rep(i,0,n)
        p1[i].id=i,p1[i].v=pa[i],p2[i].id=i,p2[i].v=pb[i]; //初始化结构体数组
 
    sort(p1,p1+n,cmp); //按亲密度排序
    sort(p2,p2+n,cmp);
 
    double maxa=p1[0].v; //A的最大亲密度
    rep(i,0,n)
    {
        if(p1[i].v!=maxa)
            break;
        else
            ans1.push_back(p1[i].id); //将亲密度最高的人的编号存入ans1
    }
 
    double maxb=p2[0].v; //B的最大亲密度
    rep(i,0,n)
    {
        if(p2[i].v!=maxb)
            break;
        else
            ans2.push_back(p2[i].id); //将亲密度最高的人的编号存入ans2
    }
 
    int len1=ans1.size();
    int f1=0;
    rep(i,0,len1)
    {
        if(pa[ans1[i]]==pa[B]) //如果与B的亲密度与A的亲密度相同，则标记f1
            f1=1;
    }
 
    int len2=ans2.size();
    int f2=0;
    rep(i,0,len2)
    {
        if(pb[ans2[i]]==pb[A]) //如果与A的亲密度与B的亲密度相同，则标记f2
            f2=1;
    }
 
    if(f1&&f2) //如果同时满足与A和B的亲密度相同的人存在，输出两个人的编号
    {
        if(sexa==-1)
            cout<<'-'<<A<<" ";
        else
            cout<<A<<" ";
        if(sexb==-1)
            cout<<'-'<<B<<endl;
        else
            cout<<B<<endl;
    }
    else //否则，分别输出与A和B亲密度最高的人的编号
    {
        rep(i,0,len1)
        {
            if(sexa==-1)
                cout<<'-'<<A<<" ";
            else
                cout<<A<<" ";
            if(fu[ans1[i]]==-1)
                cout<<'-'<<ans1[i]<<endl;
            else
                cout<<ans1[i]<<endl;
        }
        rep(i,0,len2)
        {
            if(sexb==-1)
                cout<<'-'<<B<<" ";
            else
                cout<<B<<" ";
            if(fu[ans2[i]]==-1)
                cout<<'-'<<ans2[i]<<endl;
            else
                cout<<ans2[i]<<endl;
        }
 
    }
 
    return 0;
}

以上就是并查集的知识点及相关练习了，在下一篇文章中我们将学习图的相关知识点。