栈(Stack)和队列(Queue)练习
1.栈的应用场景
1.1 逆波兰表达式求值
题目描述:
给你一个字符串数组
tokens,表示一个根据 逆波兰表示法 表示的算术表达式。请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。- 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
先来了解下中缀表达式转换为后缀表达式的小技巧!
题解:
public int evalRPN(String[] tokens) {
Stack stack = new Stack<>();
for (String x : tokens) {
if (!isOperation(x)) {
stack.push(Integer.parseInt(x));
} else {
int num2 = stack.pop();
int num1 = stack.pop();
switch (x) {
case "+":
stack.push(num1+num2);
break;
case "-":
stack.push(num1-num2);
break;
case "*":
stack.push(num1*num2);
break;
case "/":
stack.push(num1/num2);
break;
}
}
}
return stack.pop();
}
public boolean isOperation(String x) {
if (x.equals("+") || x.equals("-") || x.equals("*") || x.equals("/")) {
return true;
}
return false;
} 1.2 有效的括号
题目描述:
给定一个只包括
'(',')','{','}','[',']'的字符串s,判断字符串是否有效。有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
题解:
public boolean isValid(String s) {
Stack stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
if (ch == '(' || ch == '[' || ch == '{' ) {
stack.push(ch);
} else {
// 右括号多
if (stack.empty()) {
return false;
}
char ch2 = stack.peek();
if (ch2 == '(' && ch == ')' || ch2 == '['&& ch == ']' || ch2 == '{'&& ch == '}') {
stack.pop();
} else {
return false; // 不匹配
}
}
}
//左括号多
if (!stack.empty()) {
return false;
}
return true;
} 1.3 最小栈
题目描述:
设计一个支持
push,pop,top操作,并能在常数时间内检索到最小元素的栈。实现
MinStack类:
MinStack()初始化堆栈对象。void push(int val)将元素val推入堆栈。void pop()删除堆栈顶部的元素。int top()获取堆栈顶部的元素。int getMin()获取堆栈中的最小元素。
题解:
class MinStack {
Stack stack;
Stack minstack;
public MinStack() {
stack = new Stack<>();
minstack = new Stack<>();
}
public void push(int val) {
stack.push(val);
if (minstack.empty()) {
minstack.push(val);
}else {
if (val <= minstack.peek()) {
minstack.push(val);
}
}
}
//移出栈顶元素
public void pop() {
if (!stack.empty()) {
Integer val = stack.pop();
if (val.equals(minstack.peek())) {
minstack.pop();
}
}
}
//相当于peek
public int top() {
if (!stack.empty()) {
return stack.peek();
}
return -1;
}
public int getMin() {
return minstack.peek();
}
} 1.4 栈的压入、弹出序列
题目描述:
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。
1. 0<=pushV.length == popV.length <=1000
2. -1000<=pushV[i]<=1000
3. pushV 的所有数字均不相同
题解:
public boolean IsPopOrder (int[] pushV, int[] popV) {
Stack stack = new Stack<>();
int j = 0;
for (int i = 0; i < pushV.length; i++) {
stack.push(pushV[i]);
//会进行多次匹配选用while,避免出现越界异常,和空指针异常
while (j < popV.length && !stack.empty() && stack.peek().equals(popV[j])) {
stack.pop();
j++;
}
}
return stack.empty();
} 2. 设计循环对列
具体解题思路,就不再演示,想了解的可以看上篇文章讲解!
public class MyCircularQueue {
/*
* 设计循环队列
* */
private int[] elem;
private int front;// 队列的头
private int rear; // 队列的尾
public MyCircularQueue(int k) {
//如果采用牺牲空间 这里必须进行k+1处理
this.elem = new int[k+1];
}
/*
* 入队
* */
public boolean enQueue(int value) {
if (isFull()) {
return false;
}
elem[rear] = value;
//rear++;
rear = (rear+1) % elem.length;
return true;
}
/*
* 出队
* */
public boolean deQueue() {
if (isEmpty()) {
return false;
}
//front++;
front = (front+1) % elem.length;
return true;
}
/*
* 获取对首元素
* */
public int Front() {
if (isEmpty()) {
return -1;
}
return elem[front];
}
/*
* 获取队尾元素
* */
public int Rear() {
if (isEmpty()) {
return -1;
}
//rear往前走
int index = (rear+elem.length-1) % elem.length;
return elem[index];
}
public boolean isEmpty() {
return rear == front;
}
/*
* 检查对列是否满
* */
public boolean isFull() {
/*if ((rear + 1) % elem.length == front) {
return true;
}
return false;*/
return (rear+1) % elem.length == front;
}
}
3. 面试题
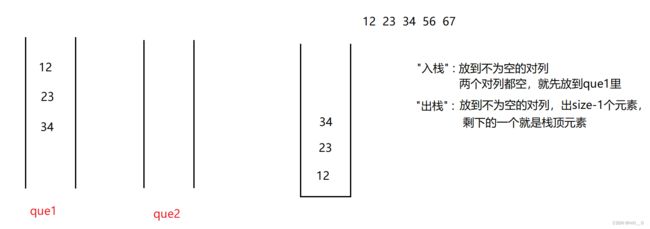
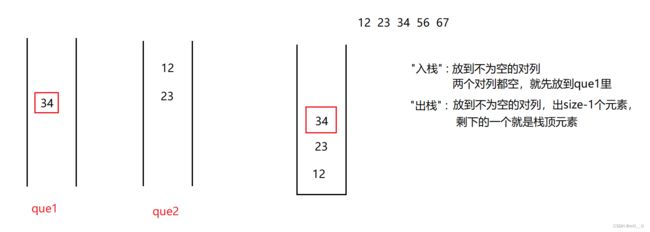
3.1 用对列实现栈
题解:
栈:先进后出 对列:先进先出
两者本身就存在互斥! 所以,要用两个对列解决!
private Queue qu1;
private Queue qu2;
public MyStack() {
qu1 = new LinkedList<>();
qu2 = new LinkedList<>();
}
public void push(int x) {
if(empty()) {
qu1.offer(x);
return;
}
if(!qu1.isEmpty()) {
qu1.offer(x);
}else {
qu2.offer(x);
}
}
public int pop() {
if(empty()) {
return -1;
}
//找到不为空的队列 出size-1个元素
if(!qu1.isEmpty()) {
int size = qu1.size();
for (int i = 0; i < size-1; i++) {
qu2.offer(qu1.poll());
}
return qu1.poll();
}else {
int size = qu2.size();
for (int i = 0; i < size-1; i++) {
qu1.offer(qu2.poll());
}
return qu2.poll();
}
}
//peek
public int top() {
if(empty()) {
return -1;
}
//找到不为空的队列 出size-1个元素
if(!qu1.isEmpty()) {
int size = qu1.size();
int tmp = -1;
for (int i = 0; i < size; i++) {
tmp = qu1.poll();
qu2.offer(tmp);
}
return tmp;
}else {
int size = qu2.size();
int tmp = -1;
for (int i = 0; i < size; i++) {
tmp = qu2.poll();
qu1.offer(tmp);
}
return tmp;
}
}
public boolean empty() {
return qu1.isEmpty() && qu2.isEmpty();
} 3.2 用栈实现对列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(
push、pop、peek、empty):实现
MyQueue类:
void push(int x)将元素 x 推到队列的末尾int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false说明:
- 你 只能 使用标准的栈操作 —— 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。- 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
题解:
private Stack stack1;
private Stack stack2;
public MyQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
public void push(int x) {
stack1.push(x);
}
public int pop() {
if (empty()) {
return -1; //栈为空,对列为空
}
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
return stack2.pop();
}
public int peek() {
if (empty()) {
return -1; //栈为空,对列为空
}
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
return stack2.peek();
}
public boolean empty() {
return stack1.isEmpty() && stack2.isEmpty();
} 标题就是链接,大家可以练习起来!!!