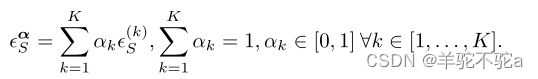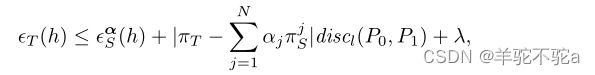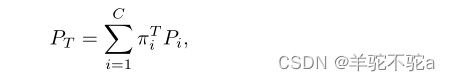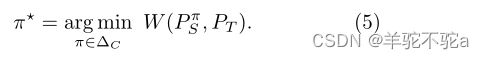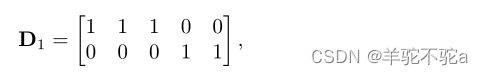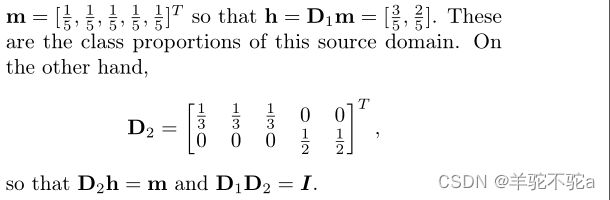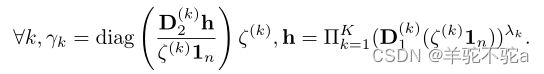【最优传输论文八】Optimal Transport for Multi-source Domain Adaptation under Target Shift

摘要

在本文中，解决了减少多个领域之间差异的问题，即多源领域自适应，并在目标转移假设下进行考虑：在所有领域中，目标是解决具有相同输出类别但具有不同标签比例的分类问题。提出的方法基于最优传输，引入的联合类比例和最优传输（JCPOT）方法通过学习未标记目标样本的类概率和允许对齐两个（或更多）概率分布的耦合，同时执行多源自适应和目标偏移校正。在合成和真实世界数据（卫星图像像素分类）任务上的实验表明，所提出的方法优于最先进的方法。

介绍

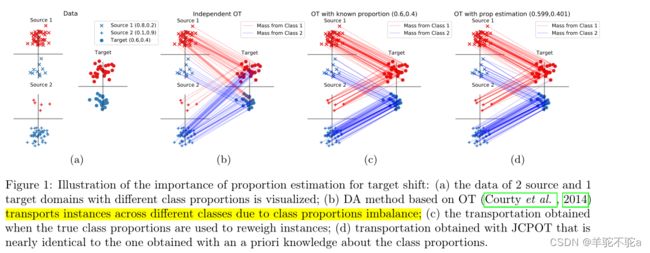
本文提出了一种基于最优传输(OT)的目标偏移校正算法。最初，OT解决了一个问题，即以一种最小化在它们之间移动单位质量的成本的方式对齐两个概率度量，同时保留原始的边际。最近出现的有效的OT公式允许其在数据处理中的应用，因为OT允许明确地学习将给定源pdf转换为目标样本的pdf。提出新的目标移位特定算法的动机源于这样一个事实，即许多流行的用于处理协变量移位的数据挖掘算法不能同样好地处理目标移位。图1说明了这一点，其中我们表明，当源域和目标域的类比例不同时，上述基于OT的数据分析方法无法限制不同类别实例之间的质量传输。然而，我们的联合类比例和最佳传输(JCPOT)模型设法正确地做到了这一点。此外，与最初的贡献相反，我们还考虑了更具挑战性的多源域适应情况，其中多个输出分布变化的源域用于学习。据我们所知，这是第一个有效利用目标移位的多源数据挖掘算法，并且随着所考虑的源域数量的增加而显示出越来越高的性能。

图1：比例估计对目标位移的重要性的说明:(a)对具有不同类比例的2个源域和1个目标域的数据进行可视化;(b)基于OT的数据处理方法(Courty et al, 2014)由于类比例不平衡而跨不同类传输实例;(c)使用真实类别比例重新权衡实例时获得的运输;(d)使用JCPOT获得的运输几乎与使用先验的类比例知识获得的运输相同

最优传输

基础知识和记号

我们定义Π(µ1，µ2)为R2上的概率分布空间，其边际为µ1和µ2，则最优输运是耦合γ∈Π(µ1，µ2)，它使以下量最小化: 

其中c(x1, x2)是将x1移动到x2的代价(分别来自分布µ1和µ2)。在该问题的离散版本中，即当µ1和µ2被定义为基于Rd中的向量的经验测度时，Π(µ1，µ2)表示矩阵γ的多角体，使得γ1 =µ1，γ t1 =µ2，前面的方程为

 

熵的正则化

在(Cuturi, 2013)中，作者向γ添加了一个正则化项，通过γ的熵来控制耦合的平滑性。离散OT的熵正则化版本是:

其中是γ的熵。

同样地，表示Kullback-Leibler散度(KL)为，可以在OT和Bregman投影之间建立以下联系。

命题1：对于，式子(2)最小值是下面Bregman投影的解

对于一个未定义的µ2，仅受边缘µ1约束，是以下封闭式投影的解: 

这种划分必须从组件的角度来理解。 根据这个命题，熵正则化的OT可以用一个基于两个边缘约束上的连续投影的简单算法来求解，并允许一个封闭形式的解。

熵正则化来源解释

 在域适应中的应用

(Courty et al, 2014)提出了一种基于OT的两域适应问题的解决方案。它包括估计源域样本的变换，使其相对于目标样本的平均位移最小，即两个域的离散分布之间的最优传输解。所提出的算法的成功是由于OT度量比数据分析中使用的其他距离(例如MMD)提供了一个重要的优势:它保留了数据的拓扑结构，并允许相当有效的估计。作者进一步添加了一个正则化术语，用于鼓励来自目标样本的实例被传输到相同类别的源样本的实例，因此由于q = 1和p = 1/2或q = 2和p = 1的范数，促进了γ的组稀疏性。

目标位移下的领域自适应

考虑一个具有K个源域的二元分类问题，每个源域由大小为， k = 1，…,K的样本表示，由概率分布得出。

其中，0 < πkS < 1, P0, P1分别为给定分类标签0和1的源数据的边际分布，P0!= P1。我们还从概率分布中得到一个大小为n的目标样本，使得。最后一个条件是先前关于该主题的理论著作中使用的目标转移的特征。

将域定义为由输入Ω的某个空间上的分布PD和标记函数fD: Ω→[0,1]组成的一对。假设类H是一组函数，∀H∈H, H: Ω→{0,1}。给定一个凸损失函数l，对于标记函数fD(也可以是假设)和假设h，相对于分布PD的真实风险定义为

在多源情况下，源和目标误差函数简写为和。那么多源数据分析的最终目标是在k个源域上学习一个假设h，该假设h在目标域中具有最佳性能。 

为此，我们将源域的组合误差定义为源域误差函数的加权和:

我们进一步用表示与分布混合物相关的标记函数。在多源场景中，为了产生用于目标域的假设，组合误差被最小化。在这里，不同的权重αk可以看作是反映相应源域分布与目标域分布接近程度的度量。 

命题2：

设H表示预测器h的假设空间:Ω→{0,1}，l为凸损失函数。令

为两个概率分布PS和PT之间的差异距离。则，对于任意固定的α和任意h∈h，成立:

其中表示组合源误差与目标误差的联合误差。 

当，∀k时，对于任意，界内的第二项都可以最小化。这可以通过对源域中的类分布进行适当的重加权来实现，但需要访问假设未知的目标比例。

在下一节中，我们建议通过最小化所有重加权源与目标分布之间的Wasserstein距离的总和来估计最优比例。为了证明这个想法，我们在下面证明了加权源分布和目标分布之间的Wasserstein距离的最小化产生最优比例估计。

接下来，让我们考虑C类的多类问题，其中目标分布定义为

其中Pi是类i∈{1，…，C}的分布。和前面一样，带加权类的源分布可以定义为 

其中π∈∆C为概率单纯形中的系数，对相应的类进行重加权。 

由于目标分布中类的比例未知，我们的目标是通过解决以下优化问题来重新权衡源类分布:

 命题3：假设。对于任意分布， 唯一解π *最小化式子(5)由给出。

这个结果直接扩展到多源情况，其中最小化所有源分布的Wasserstein距离总和的最优解是目标域比例。

由于真实分布只能通过可用的有限样本获得，因此在实践中，建议最小化经验目标分布和经验源分布之间的Wasserstein距离。这个问题的精确解与经验测度的收敛性可以用(Bobkov & Ledoux, 2016;Fournier & Guillin, 2015)，其中收敛速度与源域中可用实例的数量成反比，因此与源域的数量成反比。

联合类比例与最优运输(jcpot)

在本节中，介绍了提出的JCPOT方法，该方法旨在共同寻找最优运输计划并估计类比例。JCPOT背后的主要潜在思想是重新权衡源域中的实例，以补偿源域和目标域类比例之间的差异。

Data and Class-Based Weighting

我们假设可以访问对应于K个不同域， K = 1，…K。的几个数据集。

这些域由个实例组成，每个实例与一个感兴趣的C类相关联。在下文中，我们使用上标(k)指代其中一个源域(例如)中的量，而当指代(单个)目标域(例如µ)中的相同量时，则不使用上标。设为对应的类，即。我们还给定目标域X，由Rd中定义的n个实例填充。无监督多源自适应的目标是恢复目标域样本的类别yi，这些样本都是未知的。

JCPOT在目标移位假设下工作。对于每个源域，我们假设其数据点遵循概率分布函数或概率测度。

在现实世界中，µ(k)只能通过实例来访问，我们可以用它来定义一个分布，其中是位于的狄拉克测度，是一个相关的概率质量。将质量的对应向量记为m(k)，即， 为狄拉克测度的对应向量，则可以写成。请注意，当数据集是独立数据点的集合时，样本中所有实例的权重通常设置为相等。然而，在这项工作中，我们对源域的每个类使用不同的权重，以便我们可以调整类在目标域的比例。为此，我们注意到度量可以在C类之间分解为。我们用表示c类在X(k)中的比例。通过构造，我们有。

由于我们选择在类中具有相等的权重，我们定义了两个线性算子和，它们允许表示从质量向量m(k)到类比例h(k)的转换，并返回:

允许检索的类比例，返回的给定类比例向量的所有实例的权重，其中质量均匀分布在与一个类相关的所有数据点之间。例如，对于具有5个元素的源域，其中前3个元素属于类1，其他元素属于类2，

 

Multi-Source Domain Adaptation with JCPOT 

为此，我们建议通过求解约束Wasserstein重心问题来估计目标域中的类比例，我们使用上述定义的算子将比例与均匀加权的目标分布相匹配。相应的优化问题可写为:

正则化Wasserstein距离定义为 :

假设 λk为凸系数()，表示每个域的相对重要性。在这里，我们定义集合为每个源与目标域之间的耦合集。这一问题导致K个边缘约束 w.r.t.均匀目标分布，以及K个边缘约束与未知比例h相关。 

对前K个边际约束的优化(即)可以通过求解公式3中所示的问题来独立地对每个K进行。相反，剩下的K个约束要求对Γ和h同时求解所提出的优化问题。要做到这一点，我们将这个问题表述为一个Bregman投影，它具有规定的行和(∀k )，即:

 命题4: 式子7定义的投影解为:

初始问题现在可以通过算法1中总结的迭代Bregman投影方案来解决。算法第5行和第7行中耦合矩阵的更新可以为每个域并行计算。 

Classification in the Target Domain

当类比例和相应的耦合矩阵都得到后，需要对源样本和目标样本进行自适应，对未标记的目标样本进行分类。下面，提供可用于执行这些任务的两种可能方法。

Barycentric mapping

在(Courty et al, 2017b)中，作者提出使用OT矩阵来估计每个源实例的位置作为目标实例的重心，并由源样本的质量加权。这种方法扩展到多源设置，并自然地为每个源域的每个点提供目标对齐的位置。然后可以使用这些经过调整的源样本来学习分类器并将其直接应用于目标样本。在后续部分中，我们将使用重心映射的JCPOT的变体表示为JCPOT- pt。对于这种方法，(Courty等人，2017b)注意到过多的正则化会对新位置产生收缩效应，因为在这种配置中质量会扩散到所有目标点。此外，它需要对传输源样本进行训练的目标分类器进行估计，以提供对目标样本的预测。

Label propagation

我们建议交替使用OT矩阵在目标样本上执行标签传播。由于我们可以访问源域中的标签，并且由于OT矩阵提供了质量的传输，因此我们可以为每个目标实例测量来自每个类的质量的比例。

因此，我们建议用来估计目标样本的标签比例，其中L中的分量包含目标样本i属于c类的概率估计。注意，这种标签传播技术可以被视为增强，因为L的表达对应于来自每个源域的弱分类器的线性组合。据我们所知，这是第一次在数据分析中提出这种方法。在下面，我们用JCPOT-LP表示它，其中LP代表标签传播。

结论

在本文中，提出了一种处理目标移位的新方法JCPOT:当源和目标分布的差异是由它们的类比例的差异引起的，这是一种特殊的、尚未得到充分研究的数据分析场景。为了证明明确考虑目标位移的必要性，我们提出了一个理论结果，表明源域和目标域之间的比例不匹配导致适应效率低下。提出的方法通过解决最优运输框架中类别比例的估计和领域分布的对齐问题来解决目标移位问题。使用Wasserstein质心的思想将模型扩展到无监督数据处理场景中的多源情况。在对合成和真实数据的实验中，JCPOT方法优于当前最先进的方法，并提供了计算上有吸引力和可靠的未标记目标样本比例估计。

代码

# -*- coding: utf-8 -*-
"""
Demo AISTATS
@author: Ievgen REDKO
"""

# !/usr/bin/env python


# %% Initialization

import matplotlib
from sklearn import svm,linear_model

import json

matplotlib.use('Agg')
import os
import pylab as pl
import numpy as np
import estimproportion as prop
import sklearn
import matplotlib.pyplot as plt
import time

# import seaborn as sns

plt.ioff()  #关闭交互式绘图模式
np.random.seed(1976)
np.set_printoptions(precision=3)


'''生成双峰高斯分布数据
    centers：包含两个中心点的列表，表示两个高斯分布的中心
    sigma：标准差
    n：生成样本的数量。
    A：线性变换矩阵。
    b：偏置向量。
    h：一个包含两个比例值的列表，表示每个高斯分布的样本比例
'''
def generateBiModGaussian(centers, sigma, n, A, b, h):
    result = {}

#两个中心点生成的样本合并为一个数组 xtmp
    xtmp = np.concatenate((centers[0] + sigma * np.random.standard_normal((int(h[0] * n), 2)),
                           centers[1] + sigma * np.random.standard_normal((int(h[1] * n), 2))))
    result['X'] = xtmp.dot(A) + b

#前 int(h[0] * n) 个样本标签为0，后 int(h[1] * n) 个样本标签为1
    result['y'] = np.concatenate((np.zeros(int(h[0] * n)), np.ones(int(h[1] * n))))
    return result

'''生成具有多个源域和一个目标域的数据集，每个域都有两个类别，并且每个类别的比例是随机生成的'''
# %% Dataset generation

# nb_source+1 domains : nb_source src + 1 tgt
# all domains have two classes
# proportions for each class are generated randomly

# %% Dataset generation
ns = 500 #源域中样本数量

m1 = [-1, 0]   #两个高斯分布的中心点
m2 = [1, 0]
 
A = np.eye(2)   #线性变换矩阵
# A=np.array([[2,1],[2,-1]])

nb_sources = 20 #源域数量
h_target = [0.2, 0.8] #目标域两个类别比例
all_Xr = []  #源域数据
all_Yr = []  #源域标签
b = [0, 0]   #偏置向量
sigma = 1    #高斯分布标准差

script_dir = os.path.dirname(__file__)
results_dir = os.path.join(script_dir, 'data_prior_shift/')
if not os.path.isdir(results_dir):
    os.makedirs(results_dir)

#生成源域数据集和目标域数据集
for i in range(nb_sources):
    prop1 = np.random.randint(1, 99) / 100.0
    h_source = [prop1, round(1. - prop1, 2)] #两个类别比例和为1，四舍五入保留两位小数
    # bs = [b[np.random.randint(0,2)], b[np.random.randint(0,2)]]
    src = generateBiModGaussian([m1, m2], sigma, ns, A, b, h_source)
    all_Xr.append(src['X'])
    all_Yr.append(src['y'].astype(int))

n = 400

tgt = generateBiModGaussian([m1, m2], sigma, n, A, b, h_target)

# %%
print 'Distribution estimation'

Xt = tgt['X']
yt = tgt['y'].tolist()

possible_reg = np.logspace(-4, 1, 10) #生成一个对数等比数列，用于正则化参数的搜索空间
possible_eta = np.logspace(-4, 1, 10) #生成一个对数等比数列，用于控制标签传播算法的参数搜索空间
sources = []
nb_tr = 5
step = 3


for j in xrange(2, len(all_Xr) + 1, step):
    print 'Number of sources is ' + str(j)
    sources.append(j)

    for i in range(nb_tr):
'''计算源域和目标域之间的最佳分布比例和正则化参数'''
        reg, _, res_prop_na = prop.trueLODO(all_Xr[:j], all_Yr[:j], possible_reg, [0], 'acc', k=1)
'''通过Bregman投影估计目标域的密度分布'''
        h_res, log = prop.estimateDensityBregmanProjection(all_Xr[:j], all_Yr[:j], Xt, reg, numItermax=300)
'''计算估计的目标域密度分布与真实目标域密度分布之间的KL散度'''
        print 'Prop estimation accuracy=', float("{0:.4f}".format(prop.computeKLdiv(h_res, h_target)))
'''使用k最近邻算法基于源域数据对目标域进行标签预测'''
        estimatedy = prop.estimatekNN(all_Xr, all_Yr, Xt)
        aa = float(np.sum(tgt['y'] == estimatedy)) / len(tgt['y'])
        print ' 1NN Accuracy=', aa
'''对目标域进行标签预测'''
        estimatedy = prop.estimateLabels(all_Yr, len(tgt['y']), log)
        aa = float(np.sum(tgt['y'] == estimatedy)) / len(tgt['y'])
        print ' (Label Prop reg) w/ proportion  Accuracy=', aa

        estimatedy = prop.estimateLabelsPoints(all_Yr, Xt, log, k=1)
        aa = float(np.sum(tgt['y'] == estimatedy)) / len(tgt['y'])
        print ' (Point transport reg) w/ proportion Accuracy=', aa
'''使用源域数据和正则化参数估计源域到目标域的转移矩阵'''
        log2 = prop.estimateTransport(all_Xr, Xt, reg, numItermax=100)

        estimatedy = prop.estimateLabels(all_Yr, len(tgt['y']), log2)
        aa = float(np.sum(tgt['y'] == estimatedy)) / len(tgt['y'])
        print ' (Label Prop) 1-1 transport Accuracy=', aa

        estimatedy = prop.estimateLabelsPoints(all_Yr, Xt, log2, k=1)
        aa = float(np.sum(tgt['y'] == estimatedy)) / len(tgt['y'])
        print ' (Point transport) 1-1 transport Accuracy=', aa