第3B章 | 安徽某高校《统计建模与R软件》期末复习

第3B章  多维数据的简单统计分析

在3A章中，我们讨论的样本数据来自于一元总体X，而实际情况中许多数据来自多元数据总体，即，这时，我们通常需要分析各个变量之间的相关关系。

设为二元总体，从中取得样本，即可得样本观测矩阵为:

3B.1 二元观测样本的统计量

3B.1.1 统计量概述

1）均值：

2）X，Y的方差

3）X，Y的协方差

4）X，Y的协方差矩阵

5）X，Y的相关系数

3B.1.2 代码示例

# 生成示例数据
set.seed(123)
X <- rnorm(100)  # 示例数据：样本X
Y <- rnorm(100)  # 示例数据：样本Y

# 计算均值
mean_X <- mean(X)
mean_Y <- mean(Y)

# 计算方差
var_X <- var(X)
var_Y <- var(Y)

# 计算协方差
cov_XY <- cov(X, Y)

# 计算协方差矩阵
cov_matrix <- cov(cbind(X, Y))

# 计算相关系数
cor_XY <- cor(X, Y)

3B.2 相关性检验

3B.2.1 方法总结

关于多样本的相关性检验问题，我们通常有一下一些方法：

1）Ruben近似逼近（对总体相关系数进行区间估计）

这个函数的作用是通过样本相关系数 r 对总体相关系数 p 进行估计：

source("ruben.text.R")
ruben.test(6,0.8)

示例代码中，6是样本量，0.8是样本的相关系数。

2）Pearson相关性检验

cor.test(x,y)

3）Spearman秩相关检验

当数据不符合正态分布或关系呈非线性形式时，Pearson检验难以达到理想的效果，此时我们考虑使用非参数统计中的Spearman秩相关检验：

cor.test(x,y,method="spearman")

4）Kendall秩相关检验

Kendall秩相关检验也是一种非参数检验方法：

cor.test(x,y,method="kendall")

3B.2.2 示例代码

# 示例数据
x <- c(10, 20, 30, 40, 50)
y <- c(5, 15, 25, 35, 45)

# Pearson相关检验
result1 <- cor.test(x,y)
print(result1)

# Spearman相关检验
result2 <- cor.test(x,y, method = "spearman")
print(result2)

# Kendall秩相关检验
result3 <- cor.test(x, y, method = "kendall")
print(result3)

运行结果如下：

在输出结果中，如果 p 值小于显著性水平（通常为0.05），就可以拒绝零假设，说明两个变量之间存在显著的相关性。如果 p 值大于显著性水平，则无法拒绝零假设，表明两个变量之间可能没有显著的相关性。

3B.3 多元数据的图像绘制

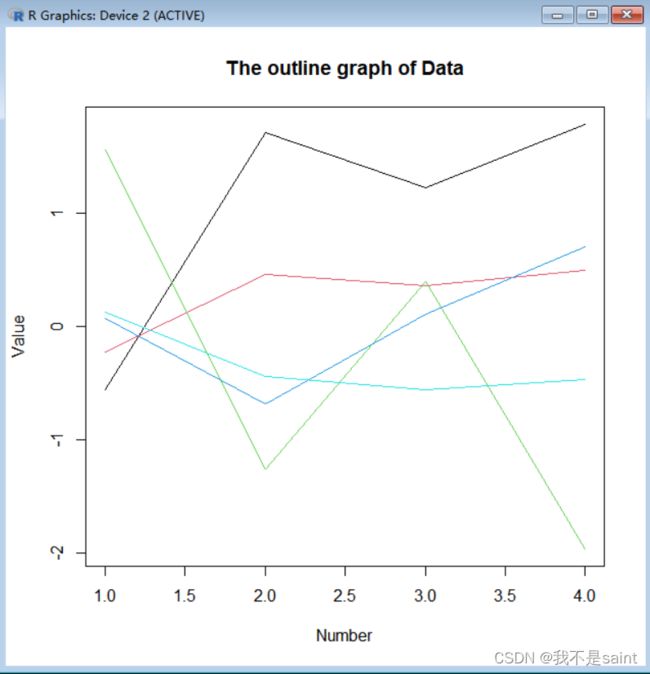
3B.3.1 轮廓图

我们可以用outline函数来绘制多元变量的轮廓图，outline并非R语言标准库函数，我们可以把它写入R语言程序脚本中：

outline <- function(x, txt=TRUE) {
   # x is a matrix or data frame of data
   if (is.data.frame(x) == TRUE)
      x <- as.matrix(x)
   m <- nrow(x); n <- ncol(x)
   plot(c(1, n), c(min(x), max(x)), type="n", 
        main="The outline graph of Data",
        xlab="Number", ylab="Value")
   for (i in 1:m) {
      lines(x[i,], col=i)  # 第i行为一条折线
      if (txt == TRUE) {
         k <- dimnames(x)[[1]][i]  # 第i条记录的名字
         text(1 + (i - 1) %% n, x[i, 1 + (i - 1) %% n], k)  # 贴近各线加标签
      }
   }
}

然后我们引入示例数据进行试验：

# 示例数据
set.seed(123)
data <- matrix(rnorm(20), ncol = 4)

# 绘制轮廓图
outline(data)

结果如下：

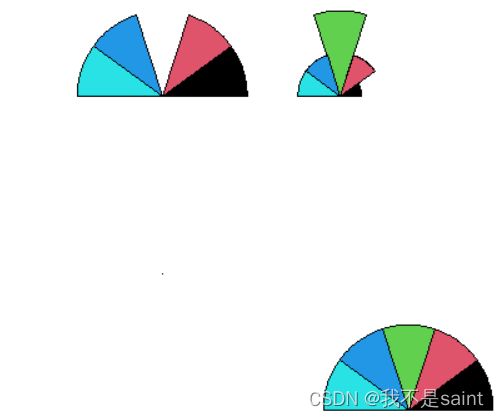
3B.3.2 星图

星图的主要目的是展示多个维度或变量之间的相对关系，以及每个变量的相对大小。每个变量的值表示为从中心点向外放射的一条线段或射线。这样一来，可以在一个图表中同时比较多个变量的相对大小，以便于观察它们的趋势和关系。我们可以引入stars包来使用stars函数：

# 安装并加载stars包
install.packages("stars")
library(stars)

# 示例数据
data <- matrix(c(80, 70, 60, 90, 85,
                 50, 60, 70, 80, 75,
                 40, 50, 60, 70, 65), ncol = 5, byrow = TRUE)

# 创建星图
stars(data, full = FALSE, draw.segments = TRUE, key.loc = c(5, 0.5), mar = c(2, 0, 0, 0))

1. full： 一个逻辑值，指示是否在星图中包含一条连接所有点的线段。如果为 TRUE，则包含，如果为 FALSE，则不包含。

2. draw.segments： 一个逻辑值，指示是否在星图中绘制从中心到每个点的线段。如果为 TRUE，则包含，如果为 FALSE，则不包含。

3. key.loc： 一个包含两个值的数值向量，表示星图中键的位置。例如，c(5, 0.5) 表示键的位置在星图的右上角，键的高度占星图高度的50%。

4. mar： 一个数值向量，包含四个边距的数值，分别表示下、左、上、右边距。例如，c(2, 0, 0, 0) 表示底部边距为2，其余为0。

运行结果如下：

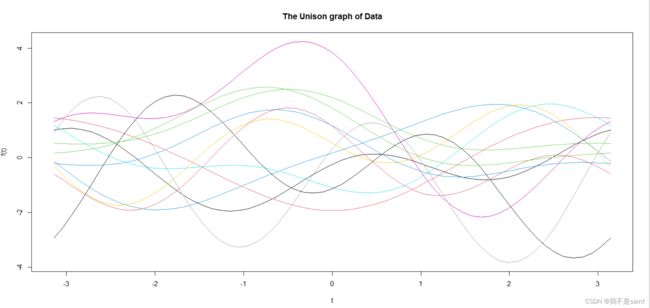
3B.3.3 调和曲线图

调和曲线图是一种用于可视化和分析时间序列数据中的周期性变化的图表。这种图表通常用于揭示数据中的周期性模式、季节性变化以及其他时间相关的趋势。在R语言中，我们可以定义一个unison函数来绘制调和曲线图：

unison <- function(x) {
   # x is a matrix or data frame of data
   if (is.data.frame(x) == TRUE)
      x <- as.matrix(x)
   t <- seq(-pi, pi, pi/30)
   m <- nrow(x); n <- ncol(x)
   f <- array(0, c(m, length(t)))
   for (i in 1:m) {
      f[i,] <- x[i, 1] / sqrt(2)
      for (j in 2:n) {
          if (j %% 2 == 0) 
             f[i,] <- f[i,] + x[i, j] * sin(j/2 * t)
          else
             f[i,] <- f[i,] + x[i, j] * cos(j %/% 2 * t)
      } 
   }
   plot(c(-pi, pi), c(min(f), max(f)), type="n", 
        main="The Unison graph of Data",
        xlab="t", ylab="f(t)")
  for (i in 1:m) lines(t, f[i,], col=i)
}

我们引入示例数据：

# 示例数据
set.seed(123)
data <- matrix(rnorm(60), ncol = 5)

# 绘制 Unison 图
unison(data)

运行结果如下：

（个人总结，如有谬误或需要改进之处欢迎联系作者）

【预告：第4章 | 安徽某高校《统计建模与R软件》期末复习（12月22日）】