三角网格表面高斯曲率的计算与可视化
所谓曲面上某点的高斯曲率,即该点两个主曲率的乘积。把曲面上的顶点映射到单位球的球心,把法线的端点映射到球面上,即将曲面上的点与球面上的点建立了一种对应,叫做曲面的球面表示,也叫高斯映射。高斯曲率的几何意义,即 球面上的面积/曲面局部面积 的极限,可以看出,高斯曲率确实反映了曲面局部的弯曲程度。

利用高斯曲率的正负性,可以很方便地研究曲面在一点邻近的结构,高斯曲率K>0为椭圆点,K<0为双曲点,K=0为平面或抛物点。并且高斯曲率是曲面的内蕴量,只与曲面的第一基本型相关,与坐标轴的选取和参数化表示无关。
言归正传,求解三角网格表面的高斯曲率,就需要利用离散微分几何,我采用的公式为:

这个公式的几何意义是比较直观的,2*Pi-该点邻域三角形对应的角度和,再除以相应区域的面积,就刻划了该点曲面的弯曲程度。

其实推导出上述公式的方法是非常巧妙的,仔细研究一下,它利用了在高斯映射的几何意义下,离散高斯曲率对局部曲面的积分
考虑p点邻域法线映射到单位球上的面积,即近似为 2*Pi-该点邻域三角形对应的角度和
不仔细写了,大家看看下面这张图,感受一下这个公式的美妙:

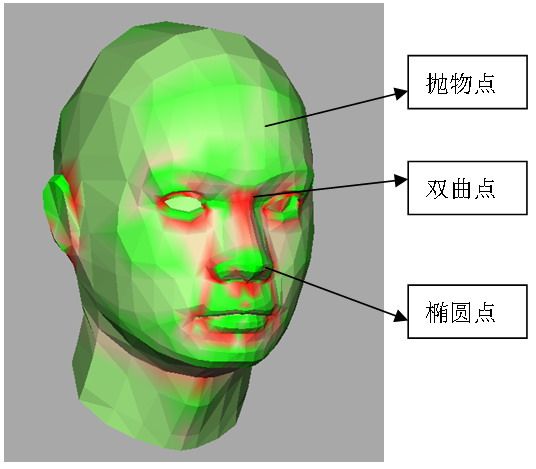
具体的编码比较简单,求出GaussCurvature数组后,归一化到[0,1],设定三种颜色c1灰黄,c2绿,c3红,线性加权伪彩显示。K>0显示为绿色,K<0显示为红色,K=0显示为灰黄色,颜色越鲜艳,高斯曲率的绝对值越大。实现效果如下图

显示效果不好,搞过图像处理的人就知道了,需要做一个直方图均衡

这样的效果就好多了,鼻梁处红色的为典型的双曲点(两个主曲率异号,主方向的两条法截线,一条向法线的正向弯曲,一条向法线的反向弯曲,形成马鞍面),鼻尖处绿色的为典型的抛物点(两个主曲率同号,曲面沿所有方向都朝向同一侧弯曲),脑门处较平坦的区域(有一个主曲率接近0)高斯曲率的绝对值较小,颜色也比较淡。
贴出更多的试验图片,计算高斯曲率并伪彩显示,确实可以直观地看出曲面的一些属性,应该可以指导网格去噪、平滑、简化、分割等后继的研究

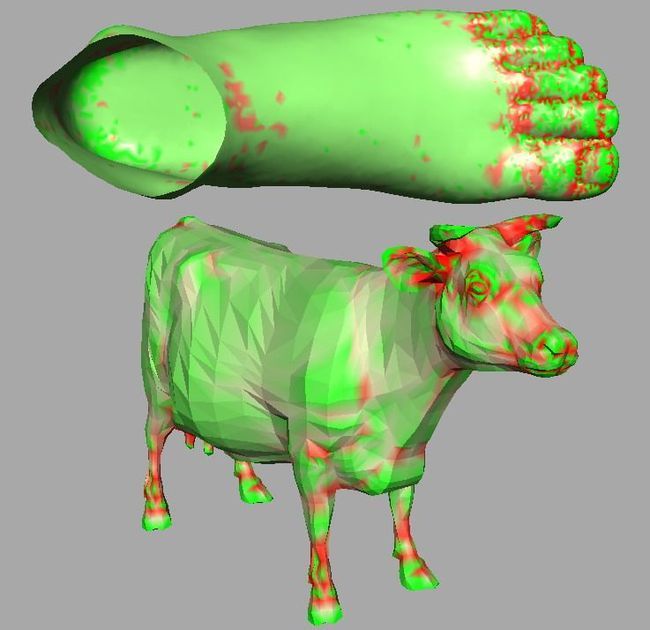
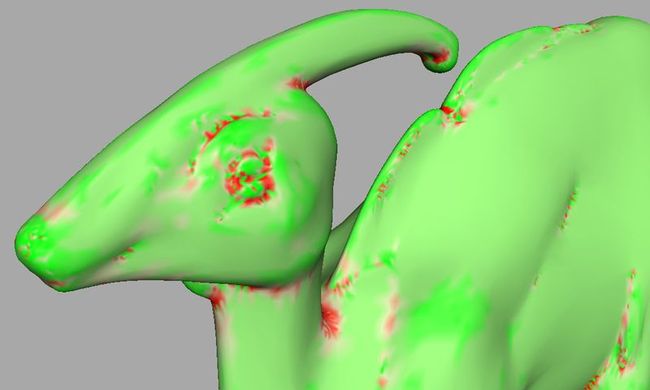

三角网格上离散高斯曲率的计算公式比较简单,做了这个简单的练习,把网格表面顶点属性可视化的程序框架搭建好了。以后有机会也可以实现一下平均曲率,主曲率,主方向的计算。