【OI/线段树】线段树知识点和例题总结

我们经常会遇到需要维护一个序列的问题，例如，给定一个整数序列，每次操作会修改序列某个位置上的数，或询问序列中某个区间所有数的和。

线段树是什么？

线段树用来处理类似上述问题，在序列上单点修改、区间询问（或者区间修改单点询问，区间修改区间询问）的一种数据结构，可以在$O(nlogn)$的时间下解决。

线段树是一棵二叉树，每个节点对应的是序列的一段区间。

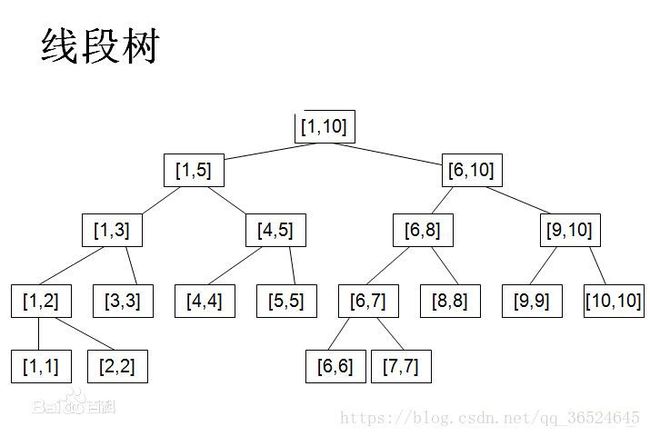
根节点对应的是$[0,n-1]$
若一个节点对应的区间$[l,r]$，当$l=r$时，就是叶节点。没有儿子，不然一定有两个儿子。
令$mid=(l+r)/2$，则左儿子对应的区间$[l,mid]$，右儿子对应的区间$[mid+1,r]$。
最有一层有$n$个节点，倒数第二层有$n/2$个节点，则一共有$2n-1$个节点。
令高度为$h$，不难看出$h$只有$O(logn)$级别。当我们需要维护序列长度为$2$的整次幂时，线段树是一棵满二叉树。其他情况下前$h-1$层是满二叉树，最后一层可能不满。

怎么建树？

我们可以发现，节点$i$的权值=它的左儿子权值+它的右儿子权值。
根据这个思路，我们就可以建树了，我们设一个结构体$tree$，$tree[i].l$和$tree[i].r$分别表示这个点代表的线段的左右下标，$tree[i].sum$表示这个节点表示的线段和。

struct node{
   
	long long l,r,sum;
}tree[N*4];//开四倍

设$build(p,l,r)$表示它的构建$[l,r]$的线段树，$p$表示区间对应的标号。两个子节点可以通过递归$build(p\ast 2,l,mid)$和$build(p\ast 2+1,mid+1,r)$得到，它的区间最小值就是两个儿子的区间最小值中的较小者。因为节点个数是$n\ast 2$级别的，所以整个流程时间复杂度是$O(n)$级别的。

void build(long long p,long long l,long long r){
    //建树
	//p表示当前节点的编号，[l,r]为区间
	tree[p].l=l;tree[p].r=r;
	if(l==r) return; //这个是叶子节点，退出递归。
	long long mid=(l+r)/2;//取中间值
	build(p*2,l,mid);//构造左子树
	build(p*2+1,mid+1,r);//构造右子树
}
build(1,1,n);//调用入口

实现单点修改

单点修改是一条形如“$Pxv$”的指令，表示把$A[x]$改为$v$

在线段树中，根节点是执行各种指令的入口。我们需要从根节点出发，递归找到$[x,x]$的叶节点，然后从下往上更新$[x,x]$以及它的所有祖先节点上保存的信息，时间复杂度为$O(logN)$

void modify(long long p,long long x,long long v){
   
	if(tree[p].l==x&&tree[p].r==x){
   tree[p].sum=v;return;}//找到叶节点
	long long mid=(tree[p].l+tree[p].r)/2;
	if(x<=mid) modify(p*2,x,v);    //x属于左半区间 
	else modify(p*2+1,x,v);  //x属于右半区间
	tree[p].sum=max(tree[p*2].v,tree[p*2+1].sum);
}
modify(1,x,y);//调用入口

实现区间查询

区间查询是一条形如$Ulr$的指令，例如查询序列$A$在$[l,r]$上的最大值，我们只需要从根节点开始，递归执行下列过程。
$1.$若$[l,r]$完全覆盖当前节点代表的空间，立刻回溯，并且该节点的$sum$为候选答案。
$2.$若左子节点与$[l,r]$有重叠部分，则递归访问左子节点
$3.$若右子节点与$[l,r]$有重叠部分，则递归访问右子节点
$O(logN)$

long long query(long long u,long long l,long long r){
   
	if(tree[u].l>=l&&tree[u].r<=r) return tree[u].sum;//完全包含
	long long mid=(tree[u].l+tree[u].r)/2;
	long long v=-(1<<30);//负无穷大
	if(l<=mid) v=query(u<<1,l,r);//左子节点有重叠 u<<1相当于u*2
	if(r>mid) v=max(v,query(u<<1|1,l,r));//右子节点有重叠
	return v;
} 

对时间复杂度的证明

该查询过程会把询问区间$[l,r]$分成$logN$个节点，取他们的最大值当做答案。
为什么可以分成$lo$