数据结构(用数组模拟链表,队列,栈,KMP,Trie树,并查集的基本模板)
南昌理工acm暑假集训
本周仅学习了部分数据结构模板和做了写模板题
下周将剩余数据结构(两节)学完并刷题巩固。
链表
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构,链表比较方便插入和删除操作。
以数组模拟链表
优点:
好理解、不需要直接处理指针更不容易 RE
1.单链表:
链表初始化
const int N=1e5+10;
int head,ne[N],e[N],idex;//head头节点,ne[N]指向下一个节点,idex指处理到的位置
void init()//初始化
{
idex=0;
head=-1;
}
在链表中头节点和k节点插入p值
void add_head(int p)//将p插入头节点
{
e[idex]=p;
ne[idex]=head;
head=idex++;
}
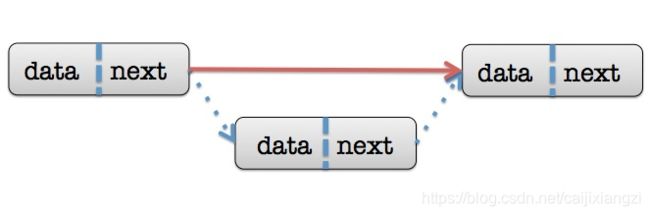
void add(int k,int p) //将p插入到下标k节点后
{
e[idex]=p;
ne[idex]=ne[k];
ne[k]=idex++;
}
解释一下 就先把点k-1的next指向新插入的p点,将新插入的next指向k,让idx向下移一位;

删除下标是k点后面的点
void remove(int k)//删除下标是k点后面的点
{
ne[k]=ne[ne[k]];
}
先遍历到指定节点的前一个节点,然后通过将前一个节点的next指针指向指定节点的下一个节点,达到悬空指定节点的效果,然后删除指定节点即可。
2.双链表
双向链表(双链表)是链表的一种。和单链表一样,双链表也是由节点组成,它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。一般我们都构造双向循环链表。
双链表初始化
void ini()
{
//一开始左边界节点指向右边界节点,右边界节点指向左边界节点
r[0]=1;
l[1]=0;
//更新节点索引
index=2;
}
双链表的插入操作
void insert(int k,int x)//在第k个节点后插入x
{
//将值赋给新节点
value[index]=x;
//将新节点分别指向插入位置的右节点和左节点
r[index]=r[k];
l[index]=k;
//将新节点右边一节点向左指向新节点,将新节点左边一节点向右指向新节点
l[r[k]]=index;
r[k]=index;
//更新节点索引
index++;
}
双链表的删除操作
void remove(int k)
{
//删除第k个节点,第k-1的右指针指向原先第k个节点的右指针指向的节点
r[l[k]]=r[k];
//删除第k个节点,原先第k个节点的右指针指向的节点的左指针指向原先第k个节点的左指针指向
//的节点
l[r[k]]=l[k];
}
栈
1、栈(Stack)是一种线性存储结构,它具有如下特点:
(1)栈中的数据元素遵守“先进后出"(First In Last Out)的原则,简称FILO结构。 (后进先出的叫法,也是可以的)
(2)限定只能在栈顶进行插入和删除操作。
2、栈的相关概念:
(1)栈顶与栈底:允许元素插入与删除的一端称为栈顶,另一端称为栈底。
(2)压栈:栈的插入操作,叫做进栈,也称压栈、入栈。
(3)弹栈:栈的删除操作,也叫做出栈。
基于数组的栈——以数组为底层数据结构时,通常以数组头为栈底,数组头到数组尾为栈顶的生长方向
1.模拟栈模板为
// tt表示栈顶
int stk[N], tt = 0;
// 向栈顶插入一个数
stk[ ++ tt] = x;
// 从栈顶弹出一个数
tt -- ;
// 栈顶的值
stk[tt];
// 判断栈是否为空
if (tt > 0)
{
}
模板题acwing模拟栈
题解:
#include2.单调栈
单调栈是一种特殊的栈,特殊之处在于栈内的元素都保持一个单调性。
假设下图是一个栈内元素的排列情况(单调递增的栈)
其功能为:利用单调栈可以找出从左/右遍历第一个比它小/大的元素的位置;
模板题:acwing单调栈
这道题的思路为:
单调递增栈,当元素可以入栈时将栈顶元素与待入栈元素进行比较,如果栈顶元素大于当前待入栈元素则出栈,否则栈顶元素便是它左边第一个比它小的元素
过程模拟为:

题解代码:
#include单调栈的模板为:
模板:
常见模型:找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
while (tt && check(stk[tt], i)) tt -- ;
stk[ ++ tt] = i;
}
队列
1、队列(Queue)与栈一样,是一种线性存储结构,它具有如下特点:
(1)队列中的数据元素遵循“先进先出”(First In First Out)的原则,简称FIFO结构;
(2)在队尾添加元素,在队头删除元素。
2、队列的相关概念:
(1)队头与队尾: 允许元素插入的一端称为队尾,允许元素删除的一端称为队头;
(2)入队:队列的插入操作;
(3)出队:队列的删除操作。
以数组作为底层数据结构时,一般讲队列实现为循环队列。这是因为队列在顺序存储上的不足:每次从数组头部删除元素(出队)后,需要将头部以后的所有元素往前移动一个位置,这是一个时间复杂度为O(n)的操作。
1.模拟队列的模板为:
// hh 表示队头,tt表示队尾
int q[N], hh = 0, tt = -1;
// 向队尾插入一个数
q[ ++ tt] = x;
// 从队头弹出一个数
hh ++ ;
// 队头的值
q[hh];
// 判断队列是否为空
if (hh <= tt)
{
}
模板题:acwing模拟队列
题解:
#include2.单调队列
用来维护一段区间内的单调上升/下降性质,导出性质就是也可以用来维护一个区间内的最值。
单调队列模板为:
模板
常见模型:找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
while (hh <= tt && check_out(q[hh])) hh ++ ; // 判断队头是否滑出窗口
while (hh <= tt && check(q[tt], i)) tt -- ;
q[ ++ tt] = i;
}
模板题:acwing滑动窗口
题目思路:
输出窗口内的最小值,可以建立一个单调递增队列,对列中存储元素的索引。
当窗口滑动后:
如果队头元素滑出了窗口,头尾元素出队。
如果新滑入的元素比队尾保存的索引对应的元素小,则队尾出队。直到新滑入的元素比队尾保存的索引对应的元素大。然后队尾入队。
当窗口全部滑入数组后,开始输出,队头保存的就是窗口内的最小元素。
最大值与最小值的处理过程类似。
思路过程模拟为
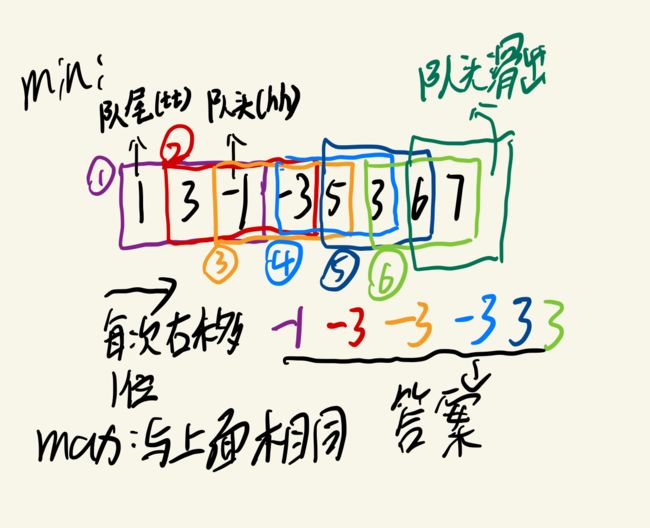
题解代码为:
#includeKMP
KMP算法之前有写过粘个模板吧
// s[]是长文本,p[]是模式串,n是s的长度,m是p的长度
求模式串的Next数组:
for (int i = 2, j = 0; i <= m; i ++ )
{
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j ++ ;
ne[i] = j;
}
// 匹配
for (int i = 1, j = 0; i <= n; i ++ )
{
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == m)
{
j = ne[j];
// 匹配成功后的逻辑
}
}
KMP主要是解决字符串匹配问题利用已经部分匹配这个有效信息,保持i指针(主串)不回溯,通过修改j指针,让模式串尽量地移动到有效的位置
Trie树
高效的储存和查找字符串集合的数据结构
Trie树,又称字典树、单词查找树、前缀树,是一种哈希树的变种,应用于字符串的统计与排序,经常被搜索引擎系统用于文本词频统计。优点是查询快,利用字串的公共前缀来节省存储空间,最大限度的减少无谓的字串比较。对于长度为m的键值,最坏情况下只需花费O(m)的时间。
先粘模板:
int son[N][26], cnt[N], idx;
// 0号点既是根节点,又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量
// 插入一个字符串
void insert(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) son[p][u] = ++ idx;
p = son[p][u];
}
cnt[p] ++ ;
}
// 查询字符串出现的次数
int query(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
依照题目来理解Trie字典树
模板题Trie字符串统计
思路图:

题解代码:
//Trie树:高效的储存和查找字符串集合的数据结构
#include并查集
并查集:(union-find sets)是一种简单的用途广泛的集合. 并查集是若干个不相交集合,能够实现较快的合并和判断元素所在集合的操作,应用很多。一般采取树形结构来存储并查集,在合并操作时可以利用树的节点树或者利用一个rank数组来存储集合的深度下界–启发式函数,在查找操作时进行路径压缩使后续的查找操作加速。这样优化实现的并查集,空间复杂度为O(N),建立一个集合的时间复杂度为O(1),N次合并M查找的时间复杂度为O(M Alpha(N)),
并查集常用使用问题:(时间复杂度近乎o(1))
1.将两个集合合并
2. 询问两个元素是否在一个集合中
模板基本原理:每个集合用一颗树来表示。树根的编号就是整个集合的编号。每个节点储存它的父节点,p[x]表示父节点
问题一:如何判断树根:if(p[x]==x)
问题二:如何求x的集合编号:while(p[x]!=x)x=p[x]
问题三:如何 合并两个集合:px是x的集合编号,py是y的集合编号。p[x]=y ;
核心模板为:
int find(int x)//寻找x的祖宗节点并压缩路径
{
if(a[x]!=x) a[x]=find(a[x]);
return a[x];
}
常用并查集模板:
(1)朴素并查集:
int p[N]; //存储每个点的祖宗节点
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
(2)维护size的并查集:
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
size[i] = 1;
}
// 合并a和b所在的两个集合:
size[find(b)] += size[find(a)];
p[find(a)] = find(b);
(3)维护到祖宗节点距离的并查集:
int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x)
{
int u = find(p[x]);
d[x] += d[p[x]];
p[x] = u;
}
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
d[i] = 0;
}
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题,初始化find(a)的偏移量
模板题:AcWing 836. 合并集合(已做)
AcWing 837. 连通块中点的数量 (已做)
AcWing 240. 食物链(看了n遍y总视频讲解还是不会/(ㄒoㄒ)/~~
2021年7月10号