西电计算机视觉作业二图像配准和拼接

对图像配准和拼接

ps ： 配准图片用的学校c楼饮水机的图片，想想觉得在c楼被毛概马原的日子可太累了，仅供参考

目录

对图像配准和拼接 1

1 整体思路 2

2 SIFT算法 2

2.1算法原理 2

2.2算法步骤 2

2.3代码实现 3

2.4 SIFT算法效果图 4

3 RANSAC算法匹配特征点 4

3.1RANSAC算法简介 4

3.2RANSAC基本假设 4

3.3RANSAC基本步骤 5

3.4RANSAC在图像匹配中的应用 5

3.5RANSAC匹配算法实现代码 5

3.6 RANSAC剔除错误匹配后效果图 9

4 利用图像几何变换算法实现图像变换和拼接 9

4.1几何变化基本矩阵 9

4.2基本思路 10

4.2.1获取单映性矩阵 10

4.2.2 通过单映性矩阵转化第二章图片 10

4.2.3 拼接图片 10

4.3实现代码 10

4.4 实现结果图片 11

5 总体代码 11

1 整体思路

（1）基于图像特征点提取的相关内容，选择相关特征点匹配算法（SIFT）完成特征点提取

（2）利用 RANSAC 算法实现特征点匹配

（3）利用图像几何变换算法实现图像变换和拼接

2 SIFT算法

2.1算法原理

尺度不变特征转换(Scale-invariant feature transform或SIFT)是一种电脑视觉的算法用来侦测与描述影像中的局部性特征，它在空间尺度中寻找极值点，并提取出其位置、尺度、旋转不变量。SIFT 特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、些微视角改变的容忍度也相当高。基于这些特性，它们是高度显著而且相对容易撷取，在母数庞大的特征数据库中，很容易辨识物体而且鲜有误认。

2.2算法步骤

1. 尺度空间极值检测：搜索所有尺度上的图像位置。通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点。

首先对图像进行采样，得到不同尺度的图像

在得到高斯金字塔后，利用高斯金字塔中的每组相邻两层相同位置进行相减 生成高斯差分金字塔

2. 关键点定位：在每个候选的位置上，通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度。

3. 方向确定：基于图像局部的梯度方向，分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换，从而提供对于这些变换的不变性。在完成关键点的梯度计算后，使用直方图统计邻域内像素的梯度和方向。梯度直方图将0~360度的方向范围分为36个柱(bins)，其中每柱10度。如图所示，直方图的峰值方向代表了关键点的主方向。方向直方图的峰值则代表了该特征点处邻域梯度的方向，以直方图中最大值作为该关键点的主方向。为了增强匹配的鲁棒性，只保留峰值大于主方向峰值80％的方向作为该关键点的辅方向。

4. 关键点描述：在每个关键点周围的邻域内，在选定的尺度上测量图像局部的梯度。这些梯度被变换成一种表示，这种表示允许比较大的局部形状的变形和光照变化。通过以上步骤，对于每一个关键点，拥有三个信息：位置、尺度以及方向。接下来就是为每个关键点建立一个描述符，用一组向量将这个关键点描述出来，使其不随各种变化而改变，比如光照变化、视角变化等等。这个描述子不但包括关键点，也包含关键点周围对其有贡献的像素点，并且描述符应该有较高的独特性，以便于提高特征点正确匹配的概率。

2.3代码实现

代码通过python opencv库中的内置函数来找到关键点信息kp1及其特征向量des1

再通过比较两个图像的关键点间的欧式距离来粗略实现匹配过程。

这个过程用到了flann算法，它是基于KDTree来实现找到不同点间的距离的远近的。

我们为每一个关键点都匹配一个最优点和次有点，当最优点和本身点的距离远远小于次优点与本身的距离时我们认为这个点时匹配上的好点。（及最优远远好于次优时，认为最优点是匹配上的点）

最后将匹配上的点对放入good数组中。

kp1, des1 = sift.detectAndCompute(img1gray, None)
kp2, des2 = sift.detectAndCompute(img2gray, None)
\# FLANN parameters 通过KDtree算法来找到最近点
FLANN_INDEX_KDTREE = 1
index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
search_params = dict(checks=50)
flann = cv2.FlannBasedMatcher(index_params, search_params)
matches = flann.knnMatch(des1, des2, k=2)
matchesMask = [[0, 0] for i in range(len(matches))]

good = []
pts1 = []
pts2 = []
\# 当最优点与次有点差距较大才能体现最优点的准确性
for i, (m, n) in enumerate(matches):
`    `if m.distance < 0.7 \* n.distance:
`        `good.append(m)
`        `pts2.append(kp2[m.trainIdx].pt)
`        `pts1.append(kp1[m.queryIdx].pt)
`        `matchesMask[i] = [1, 0]

2.4 SIFT算法效果图

3 RANSAC算法匹配特征点

3.1RANSAC算法简介

RANSAC是“RANdom SAmple Consensus（随机抽样一致）”的缩写。它可以从一组包含“局外点”的观测数据集中，通过迭代方式估计数学模型的参数。它是一种不确定的算法——它有一定的概率得出一个合理的结果；为了提高概率必须提高迭代次数。

3.2RANSAC基本假设

1. “内群”(inlier, 即正常数据，正确数据)数据可以通过几组模型的参数来叙述其分布，而“离群”(outlier，异常数据)数据 则是不适合模型化的数据。

2. 数据会受噪声影响，噪声指的是离群，例如从极端的噪声或错误解释有关数据的测量或不正确的假设。

3. RANSAC假定，给定一组（通常很小）的内点群，存在一个程序，这个程序可以估算最佳解释或最适用于这一数据模型的参数

3.3RANSAC基本步骤

1：假定模型（如直线方程），并随机抽取N个（以2个为例）样本点，对模型进行拟合

2：由于不是严格线性，数据点都有一定波动，假设容差范围为：sigma，找出距离拟合曲线 容差范围内的点，并统计点的个数

3：重新随机选取N个点，重复第一步~第二步的操作，直到结束迭代

4：每一次拟合后，容差范围内都有对应的数据点数，找出数据点个数最多的情况，就是最终 的拟合结果.

3.4RANSAC在图像匹配中的应用

从匹配的点对中选择8个点，使用归一化8点法估算出基础矩阵F

计算其余的点对到其对应对极线的距离dp ，若dp＜d则该点为内点，否则为外点。记下符合该条件的内点的个数为num

迭代k次，或者某次得到内点的数目num占有的比例大于等于95%，则停止。选择num最大的基础矩阵作为最终的结果。

3.5RANSAC匹配算法实现代码

def compute_fundamental(x1, x2):
`    `n = x1.shape[1]
`    `if x2.shape[1] != n:
`        `raise ValueError("Number of points don't match.")

`    `# build matrix for equations
`    `A = np.zeros((n, 9))
`    `for i in range(n):
`        `A[i] = [x1[0, i] \* x2[0, i], x1[0, i] \* x2[1, i], x1[0, i] \* x2[2, i],
`                `x1[1, i] \* x2[0, i], x1[1, i] \* x2[1, i], x1[1, i] \* x2[2, i],
`                `x1[2, i] \* x2[0, i], x1[2, i] \* x2[1, i], x1[2, i] \* x2[2, i]]

`    `# compute linear least square solution
`    `U, S, V = np.linalg.svd(A)
`    `F = V[-1].reshape(3, 3)

`    `# constrain F
`    `# make rank 2 by zeroing out last singular value
`    `U, S, V = np.linalg.svd(F)
`    `S[2] = 0
`    `F = np.dot(U, np.dot(np.diag(S), V))

`    `return F / F[2, 2]


def compute_fundamental_normalized(x1, x2):
`    `*"""    Computes the fundamental matrix from corresponding points
`        `(x1,x2 3\*n arrays) using the normalized 8 point algorithm. """*

`    `n = x1.shape[1]
`    `if x2.shape[1] != n:
`        `raise ValueError("Number of points don't match.")

`    `# normalize image coordinates
`    `x1 = x1 / x1[2]
`    `mean_1 = np.mean(x1[:2], axis=1)
`    `S1 = np.sqrt(2) / np.std(x1[:2])
`    `T1 = np.array([[S1, 0, -S1 \* mean_1[0]], [0, S1, -S1 \* mean_1[1]], [0, 0, 1]])
`    `x1 = np.dot(T1, x1)

`    `x2 = x2 / x2[2]
`    `mean_2 = np.mean(x2[:2], axis=1)
`    `S2 = np.sqrt(2) / np.std(x2[:2])
`    `T2 = np.array([[S2, 0, -S2 \* mean_2[0]], [0, S2, -S2 \* mean_2[1]], [0, 0, 1]])
`    `x2 = np.dot(T2, x2)

`    `# compute F with the normalized coordinates
`    `F = compute_fundamental(x1, x2)
`    `# print (F)
`    `# reverse normalization
`    `F = np.dot(T1.T, np.dot(F, T2))

`    `return F / F[2, 2]


def randSeed(good, num=8):
`    `*'''
`    `**:param** good: 初始的匹配点对
`    `**:param** num: 选择随机选取的点对数量
`    `**:return**: 8个点对list
`    `'''*
`    `eight_point = random.sample(good, num)
`    `return eight_point


def PointCoordinates(eight_points, keypoints1, keypoints2):
`    `*'''
`    `**:param** eight_points: 随机八点
`    `**:param** keypoints1: 点坐标
`    `**:param** keypoints2: 点坐标
`    `**:return**:8个点
`    `'''*
`    `x1 = []
`    `x2 = []
`    `tuple_dim = (1.,)
`    `for i in eight_points:
`        `tuple_x1 = keypoints1[i[0].queryIdx].pt + tuple_dim
`        `tuple_x2 = keypoints2[i[0].trainIdx].pt + tuple_dim
`        `x1.append(tuple_x1)
`        `x2.append(tuple_x2)
`    `return np.array(x1, dtype=float), np.array(x2, dtype=float)
def ransac(good, keypoints1, keypoints2, confidence, iter_num):
`    `Max_num = 0
`    `good_F = np.zeros([3, 3])
`    `inlier_points = []
`    `for i in range(iter_num):
`        `eight_points = randSeed(good)
`        `x1, x2 = PointCoordinates(eight_points, keypoints1, keypoints2)
`        `F = compute_fundamental_normalized(x1.T, x2.T)
`        `num, ransac_good = inlier(F, good, keypoints1, keypoints2, confidence)
`        `if num > Max_num:
`            `Max_num = num
`            `good_F = F
`            `inlier_points = ransac_good
`    `print(Max_num, good_F)
`    `return Max_num, good_F, inlier_points


def computeReprojError(x1, x2, F):
`    `*"""
`    `计算投影误差
`    `"""*
`    `ww = 1.0 / (F[2, 0] \* x1[0] + F[2, 1] \* x1[1] + F[2, 2])
`    `dx = (F[0, 0] \* x1[0] + F[0, 1] \* x1[1] + F[0, 2]) \* ww - x2[0]
`    `dy = (F[1, 0] \* x1[0] + F[1, 1] \* x1[1] + F[1, 2]) \* ww - x2[1]
`    `return dx \* dx + dy \* dy


def inlier(F, good, keypoints1, keypoints2, confidence):
`    `num = 0
`    `ransac_good = []
`    `x1, x2 = PointCoordinates(good, keypoints1, keypoints2)
`    `for i in range(len(x2)):
`        `line = F.dot(x1[i].T)
`        `# 在对极几何中极线表达式为[A B C],Ax+By+C=0,  方向向量可以表示为[-B,A]
`        `line_v = np.array([-line[1], line[0]])
`        `err = h = np.linalg.norm(np.cross(x2[i, :2], line_v) / np.linalg.norm(line_v))
`        `# err = computeReprojError(x1[i], x2[i], F)
`        `if abs(err) < confidence:
`            `ransac_good.append(good[i])
`            `num += 1
`    `return num, ransac_good

3.6 RANSAC剔除错误匹配后效果图

4 利用图像几何变换算法实现图像变换和拼接

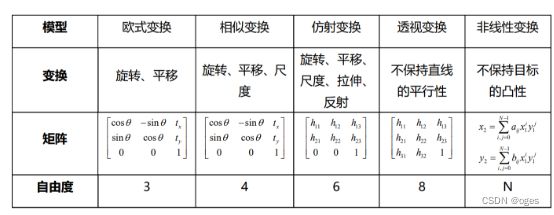
4.1几何变化基本矩阵

4.2基本思路

4.2.1获取单映性矩阵

M, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 5.0)

通过opencv中的这个findHomography函数我们可以获得到变化矩阵M

4.2.2 通过单映性矩阵转化第二章图片

warpImg = cv2.warpPerspective(testImg, M, (testImg.shape[1], testImg.shape[0]),flags=cv2.WARP_INVERSE_MAP)

通过opencv中的这个warpPerspective函数我们可以获得到变化后的图片

4.2.3 拼接图片

找到图片的重叠部分的坐标，新的图片的没有重叠部分则各自按原先图片绘制，重叠的部分用插值的方式来融合。

4.3实现代码

src_pts = np.float32([kp1[m.queryIdx].pt for m in good]).reshape(-1, 1, 2)
dst_pts = np.float32([kp2[m.trainIdx].pt for m in good]).reshape(-1, 1, 2)
M, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 5.0)  # 通过ransac算法找到单应性匹配矩阵
mask_matches = mask.ravel().tolist()
warpImg = cv2.warpPerspective(testImg, M, (testImg.shape[1], testImg.shape[0]),
`                              `flags=cv2.WARP_INVERSE_MAP)

\# 获取重叠部分
for col in range(0, cols):
`    `if srcImg[:, col].any() and warpImg[:, col].any():
`        `left = col
`        `break
for col in range(cols - 1, 0, -1):
`    `if srcImg[:, col].any() and warpImg[:, col].any():
`        `right = col
`        `break

res = np.zeros([rows, cols, 3], np.uint8)
for row in range(0, rows):
`    `for col in range(0, cols):
`        `if not srcImg[row, col].any():
`            `res[row, col] = warpImg[row, col]
`        `elif not warpImg[row, col].any():
`            `res[row, col] = srcImg[row, col]
`        `# 重叠部分用插值法融合两张图片
`        `else:
`            `srcImgLen = float(abs(col - left))
`            `testImgLen = float(abs(col - right))
`            `alpha = srcImgLen / (srcImgLen + testImgLen)
`            `res[row, col] = np.clip(srcImg[row, col] \* (1 - alpha) + warpImg[row, col] \* alpha, 0, 255)

4.4 实现结果图片

5 总体代码

 https://gitee.com/orangeinus/xd_-cs_computer_vison_2