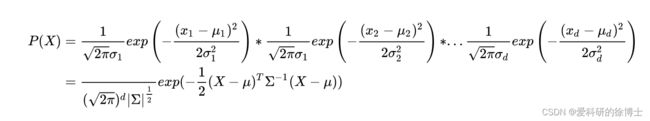【很详细】高斯分布之间的KL散度讲解+Python代码实现
文章目录
- 引言
- 高斯分布在机器学习中的重要性
- 高斯分布
-
- 一元高斯分布
- 高斯分布的 σ \sigma σ原则
- 多元高斯分布
- 高斯分布的Python实现
- 高斯分布的KL散度
- 高斯分布KL散度的Python实现
引言
最近在学习各种算法模型,经常遇到高斯分布以及KL散度的概念,通过学习网络上的各种资源,进行深入理解和整合,写一篇比较详细和系统的文章,以便自己日后查阅,也供大家学习和参考。本篇文章主要是:先介绍高斯分布在机器学习中重要性(也即为什么很多模型算法都会假设某些数据分布是服从高斯分布的呢)-----> 什么是高斯分布---->使用Python简单实现高斯分布------> 高斯分布之间的KL散度------->Python实现高斯分布的KL散度。
【推荐:非常推荐大家认认真真地读完,我相信你一定会明白整个推导过程,真的不难!不懂问我】
高斯分布在机器学习中的重要性
高斯分布在机器学习或者算法领域非常常见,也是一种非常重要的分布。相信很多小伙伴都会发现,很多模型算法都采用高斯分布来估计数据的分布,我们在此分析一下主要原因:
-
一个重要原因是它的数学性质十分优秀,它的概率密度函数具有连续性、可微性和单调性,且具有最大似然估计的性质,使得高斯分布的参数可以通过最大似然估计的方法进行估计。同时,在机器学习中,很多算法大都基于最大似然估计的原理,因此采用高斯分布作为模型的概率分布是非常合理的。
-
此外,高斯分布还有其他优秀的性质,例如满足中心极限定理,即在数据量较大时,任意一组数据的分布都接近于高斯分布。或者这样理解:对于未知的总体分布,在样本量足够大的情况下,并且知道样本均值和样本方差,可以近似服从高斯分布。或者:样本容量无穷大时,许多分布的极限就是高斯分布。这样的性质非常适用于机器学习中的数据分析和建模。
总的来说,高斯分布在机器学习中有着广泛的应用,这主要是由于它的优良的数学性质和广泛适用性所决定的。
高斯分布
既然高斯分布这么重要,那什么是高斯分布呢?它长什么样子呢?
注:高斯分布也称为正态分布
一元高斯分布
设均值为 μ μ μ,方差为 σ σ σ,则有:
 当 μ = 0 , σ = 1 μ=0,σ=1 μ=0,σ=1时,为标准高斯分布(或者标准正态分布),则有:
当 μ = 0 , σ = 1 μ=0,σ=1 μ=0,σ=1时,为标准高斯分布(或者标准正态分布),则有:
P ( z ) = 1 2 π e − z 2 2 P(z)=\frac{1}{\sqrt{2\pi}} e^{-\frac{z^2}{2} } P(z)=2π1e−2z2
即:
P ( z ) ∼ N ( 0 , 1 ) , z = x − μ σ P(z)\sim N(0,1),z=\frac{x-\mu }{\sigma } P(z)∼N(0,1),z=σx−μ
因此,根据上述公式,我们常常采用重参数化的技巧,实现从均值为 μ 标准差为 σ 的高斯分布中采样
x = μ + z ⋅ σ x=\mu +z \cdot \sigma x=μ+z⋅σ
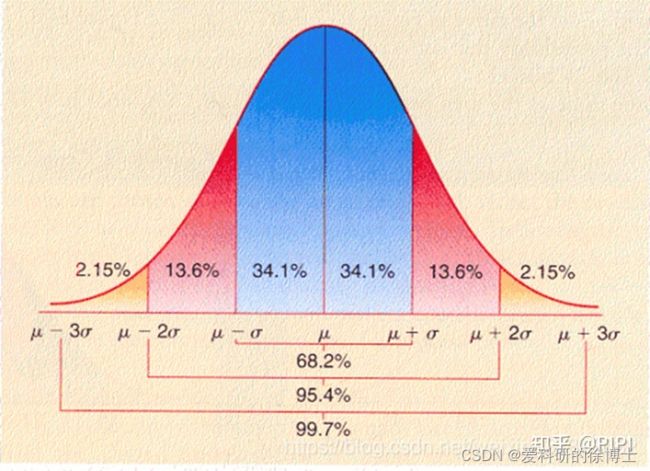
高斯分布的 σ \sigma σ原则
σ \sigma σ原则:数值分布在(μ-σ,μ+σ)中的概率为0.6526;
2 σ \sigma σ原则:数值分布在(μ-2σ,μ+2σ)中的概率为0.9544;
3 σ \sigma σ原则:数值分布在(μ-3σ,μ+3σ)中的概率为0.9974;
基本上可以把区间 ( μ − 3 σ , μ + 3 σ ) (μ-3σ,μ+3σ) (μ−3σ,μ+3σ)看作是随机变量 x x x实际可能的取值区间,落在该区间之外的概率小于千分之三。
多元高斯分布
现在我们将一元高斯分布扩展到多维空间,即假设有 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn等多个维度,同时假设多维空间中的每个维度之间都是完全独立的,则独立的 n n n元高斯分布有:

在机器学习中,我们常用的是一元高斯分布分布,因此,这里我主要以介绍一元高斯分布为主,介绍后面的内容,如果有想了解多元高斯分布的伙伴,可以给我留言~
高斯分布的Python实现
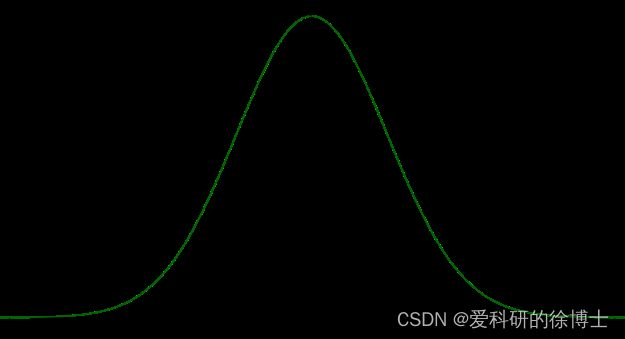
高斯分布的曲线呈钟形,因此人们又经常称之为钟形曲线。其中,高斯分布的期望值(均值) μ \mu μ决定了曲线中心位置,标准差决定了曲线的高度和宽度,标准差小,曲线”高瘦“;标准差大,曲线”矮胖“。
例如,下图是一个标准正态分布(即 μ = 0 , σ = 1 μ=0,σ=1 μ=0,σ=1)的曲线图。
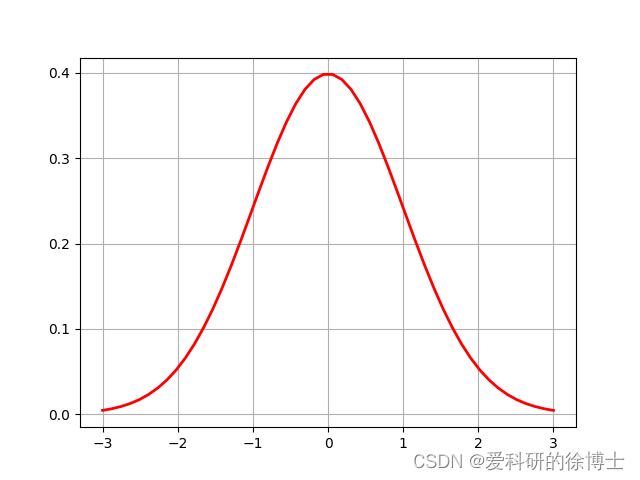
其对应的Python代码如下:
#绘制标准高斯分布
import numpy as np
import matplotlib.pyplot as plt
mu=0#均值
sigma=1#标准差
x=np.arange(mu-3,mu+3,0.2)#随机生成x变量值
#根据标准高斯分布的概率密度函数,得到每个x对应的y值
y = np.multiply(np.power(np.sqrt(2 * np.pi) * sigma, -1), np.exp(-np.power(x - mu, 2) / 2 * sigma ** 2))
#plt.rcParams['font.sans-serif'] = ['SimHei']#用来显示中文
plt.plot(x,y,'r-',linewidth=2)
plt.title("The image of Standard Gaussian Distribution")
plt.grid(True)
plt.show()
下图,是将多个高斯分布绘制在同一个画面中,这样可以对比不同高斯分布的形状
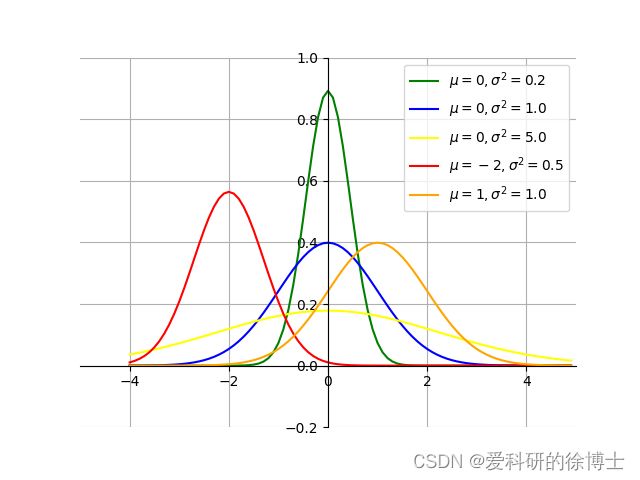
其对应的Python代码如下所示:
# ==========同时绘制多个高斯分布========
import numpy as np
import math
import matplotlib.pyplot as plt
def gauss_distribution_y(x, mu=0, sigma=1):
"""根据高斯分布的概率密度函数,计算每个由自变量x的因变量的值y
Argument:
x: array
输入数据(自变量)
mu: float
均值
sigma: float
方差
"""
left = 1 / (np.sqrt(2 * math.pi) * np.sqrt(sigma))
right = np.exp(-(x - mu) ** 2 / (2 * sigma))
return left * right
if __name__ == '__main__':
# 自变量
x = np.arange(-4, 5, 0.1)
# 因变量(不同均值或方差)
y_1 = gauss_distribution_y(x, 0, 0.2)#均值为0,标准差为0.2
y_2 = gauss_distribution_y(x, 0, 1.0)#均值为0,标准差为1.0
y_3 = gauss_distribution_y(x, 0, 5.0)#均值为0,标准差为5.0
y_4 = gauss_distribution_y(x, -2, 0.5)#均值为-2,标准差为0.5
y_5 = gauss_distribution_y(x, 1, 1.0) # 均值为1,标准差为1.0
# 绘图
plt.plot(x, y_1, color='green')
plt.plot(x, y_2, color='blue')
plt.plot(x, y_3, color='yellow')
plt.plot(x, y_4, color='red')
plt.plot(x, y_5, color='orange')
# 设置坐标系
plt.xlim(-5.0, 5.0)
plt.ylim(-0.2, 1)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data', 0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
plt.legend(labels=['$\mu = 0, \sigma^2=0.2$', '$\mu = 0, \sigma^2=1.0$', '$\mu = 0, \sigma^2=5.0$',
'$\mu = -2, \sigma^2=0.5$','$\mu = 1, \sigma^2=1.0$'])
plt.grid()
plt.show()
高斯分布的KL散度
先来看一下KL散度的定义
- KL散度(Kullback-Leibler Divergence)一般用于度量两个概率分布函数之间的“距离”,其定义如下:
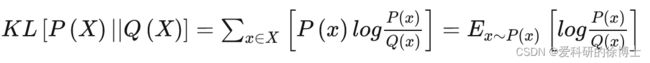 那假设两个高斯分布分别为: p 1 = N ( μ 1 , σ 1 2 ) p_1=N(\mu_1,\sigma_1^2) p1=N(μ1,σ12), p 2 = N ( μ 2 , σ 2 2 ) p_2=N(\mu_2,\sigma_2^2) p2=N(μ2,σ22),计算两者之间KL散度为:
那假设两个高斯分布分别为: p 1 = N ( μ 1 , σ 1 2 ) p_1=N(\mu_1,\sigma_1^2) p1=N(μ1,σ12), p 2 = N ( μ 2 , σ 2 2 ) p_2=N(\mu_2,\sigma_2^2) p2=N(μ2,σ22),计算两者之间KL散度为:

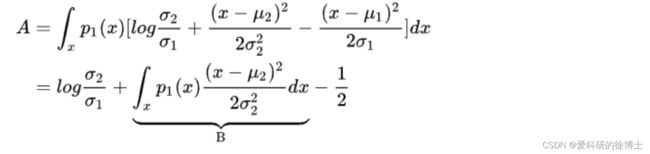
在上述公式的推导【注意,上述公式的第一行中最后一个式子有错误,应该是 ( x − μ 1 ) 2 σ 1 2 \frac{(x-\mu_1)^2}{\sigma_1^2} σ12(x−μ1)2】用到的规则有:
(1) ∫ x p 1 ( x ) d x = 1 \int _x p_1(x)dx=1 ∫xp1(x)dx=1 (即,全概率公式)
(2) ∫ x p 1 ( x ) ( x − μ 1 ) 2 σ 1 2 d x = σ 1 2 \int _x p_1(x)\frac{(x-\mu_1)^2}{\sigma_1^2}dx=\sigma_1^2 ∫xp1(x)σ12(x−μ1)2dx=σ12 (即,方差)
(3) ∫ x p 1 ( x ) ( x − μ 1 ) 2 2 σ 1 2 d x = 1 2 ∫ x p 1 ( x ) ( x − μ 1 ) 2 σ 1 2 d x = 1 2 ∗ σ 1 2 σ 1 2 = 1 2 \int _x p_1(x)\frac{(x-\mu_1)^2}{2\sigma_1^2}dx= \frac{1}{2}\int _x p_1(x)\frac{(x-\mu_1)^2}{\sigma_1^2}dx=\frac{1}{2}*\frac{\sigma_1^2}{\sigma_1^2}=\frac{1}{2} ∫xp1(x)2σ12(x−μ1)2dx=21∫xp1(x)σ12(x−μ1)2dx=21∗σ12σ12=21
接着,将转化式: x − μ 2 = ( x − μ 1 ) + ( μ 1 − μ 2 ) x-\mu_2=(x-\mu_1)+(\mu_1-\mu_2) x−μ2=(x−μ1)+(μ1−μ2)代入到式子 B B B中:
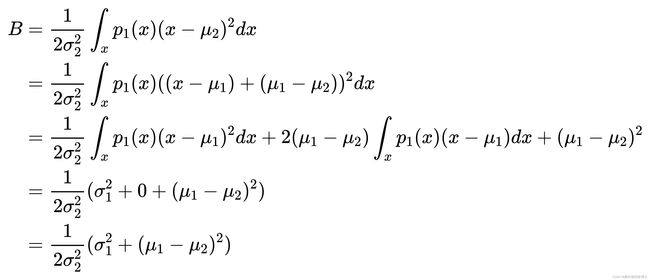 在上述公式的推导用到的规则有:
在上述公式的推导用到的规则有:
(1) ∫ x p 1 ( x ) d x = 1 \int _x p_1(x)dx=1 ∫xp1(x)dx=1 (即,全概率公式)
(2) ∫ x p 1 ( x ) ( x − μ 1 ) 2 σ 1 2 d x = σ 1 2 \int _x p_1(x)\frac{(x-\mu_1)^2}{\sigma_1^2}dx=\sigma_1^2 ∫xp1(x)σ12(x−μ1)2dx=σ12 (即,方差)
(2) ∫ x p 1 ( x ) x d x = μ 1 \int _x p_1(x)xdx=\mu_1 ∫xp1(x)xdx=μ1 (即,均值)
综合上述推导,最终得到:
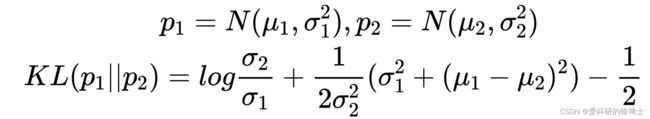 当我们假设 p 2 p_2 p2服从标准高斯分布时,即 p 2 = N ( 0 , 1 ) p_2=N(0,1) p2=N(0,1),则有:
当我们假设 p 2 p_2 p2服从标准高斯分布时,即 p 2 = N ( 0 , 1 ) p_2=N(0,1) p2=N(0,1),则有:
K L ( N ( μ , σ 2 ) ∣ ∣ N ( 0 , 1 ) ) = − 1 2 × ( 2 l o g σ + 1 − σ 2 − μ 2 ) KL(N(\mu,\sigma^2)||N(0,1))=-\frac{1}{2}\times (2log{\sigma}+ 1-\sigma^2-\mu^2) KL(N(μ,σ2)∣∣N(0,1))=−21×(2logσ+1−σ2−μ2)
高斯分布KL散度的Python实现
Python的实现还是非常简单的,关键是上面的公式推导
#高斯KL散度
import torch
def Gaussi_KL_loss(mu,logvar):
"""
mu: latent mean 均值
logvar: latent log variance 方差的对数
"""
KLD = -0.5 * torch.sum(logvar + 1 - mu.pow() - logvar.exp())
return KLD
【注:】(1)在这个公式中 l o g v a r logvar logvar表示 l o g σ 2 log\sigma^2 logσ2;
(2)在实际应用,mu和logvar一般都是向量,所以,在KLD公式中有一个torch.sum()运算,表示对向量中的每一维都计算高斯KL散度,最后求和;有的地方也会使用torch.mean(),即取平均运算
欢迎留言交流!