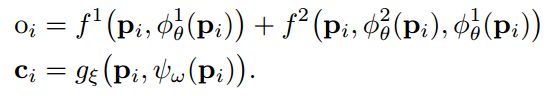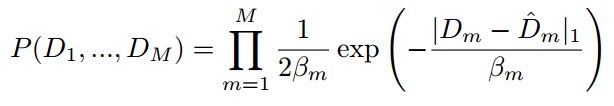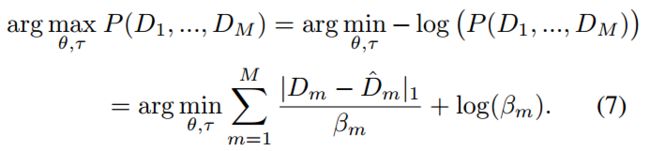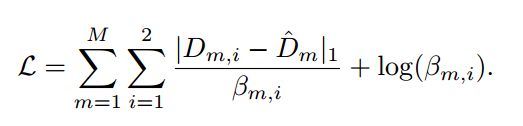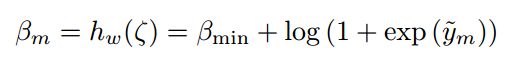【文献分享】UncLe-SLAM: 将不确定性学习用于密集神经SLAM
论文题目:UncLe-SLAM: Uncertainty Learning for Dense Neural SLAM
中文题目:UncLe-SLAM: 将不确定性学习用于密集神经SLAM
作者:Erik Sandstrom Kevin Ta Luc Van Gool Martin R.Oswald
0 笔者个人体会
这篇文章也是NeRF+SLAM系列,可以是NICE-SLAM的延伸,NICE-SLAM的基础上做了很多的改进,仔细读这篇文章是有很多收获的:
- 大量的研究调查:这篇文章引用了81篇参考文献,在相关工作阶段也是对各个相关领域都开展了广泛的研究,算法各个部分也有严格证明。
- 大量的实验验证:作者不仅在正文部分开展大量使用,在附录部分也展示了全方位的比较实验。
- 自监督学习:本篇文章不需要地面真值进行训练,而是具备了自监督学习能力,这提高了NeRF-SLAM的泛化能力
- 更像SLAM:NICE-SLAM作者提到,与传统SLAM相比,定位性能还是有所不足,而在实验中可以看出,本文算法在跟踪性能上相比于NICE-SLAM有大幅提高,在下面的效果展示也可以看到,但是没有与传统SLAM方法进行比较,可能还是有所不足?但是也是往前迈了一大步的。
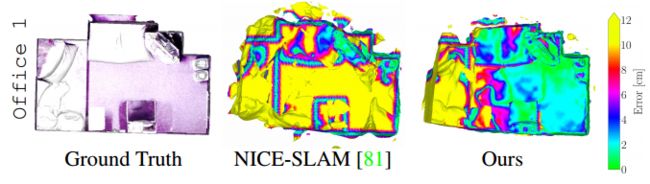
1 效果展示
2 引言
本文提出了一种用于密集神经SLAM的不确定性学习框架,该框架可以仅从2D输入数据中以自监督的方式进行训练,进一步讨论了多传感器输入情况下不确定性学习的优点,本文的方法可以自然地拓展到多传感器融合中。
本文主要贡献:
- 提出了一种估计单传感器和多传感器情况下任意深度不确定性的鲁棒方法。引入的框架鲁棒、准确,可以直接集成到密集的SLAM系统中,而不需要地面真值深度。
- 在单个深度传感器的情况下,提出的不确定性驱动的方法经常提高有关几何重建和跟踪精度的标准性能指标。在多传感器情况下,对于各种传感器组合,提出的方法获得的结果始终优于从单个传感器获得的结果。
3 算法框架
3.1 准备工作-NeRF原理
这一部分主要先阐述了NeRF的工作原理,大部分延用了NICE-SLAM的算法,由于这不是本文重点,这部分仅做简略解释。
分层场景表示:中间层和精细层分别对应一个解码器 f l , l ∈ { 1 , 2 } f^l,l\in\{1,2\} fl,l∈{1,2},同样有一个解码器 g ξ g_\xi gξ将颜色编码在第四个特征网格中,用于几何优化初始阶段后的进一步场景细化。观测到的场景几何由中分辨率和精细分辨率特征网格重构,精细特征网格输出残差加入到中分辨率特征网格占用中。综上所述,预测占用率 o i o_i oi和颜色 c i c_i ci为:
之后进行ray-trace,沿光线方向r采样一系列的点 p i p_i pi:
然后通过以下公式计算出体密度(占用率),该权重表示射线在该特定点终止的离散概率:
由此,我们也可以计算出均值和方差:
3.2 理论假设
作者将每条射线建模为拉普拉斯噪声分布,有文献证明在视觉任务上,这种假设比高斯假设表现得更好。此外,坐着假设噪声是异方差的,这意味着噪声方差是每个像素的一个变量。因此,测量的深度是从概率密度函数中采样的:
D m ^ \hat{D_m} Dm^是深度真值, β m \beta_m βm是由后面的不确定性估计计算得到的标准差,由于每个像素是独立的,我们可以得到:
然后通过极大似然估计,我们可以得到最优估计:
附上一些笔者的理解: 本文方法能实现自监督在线训练,做法就是:他们对输入深度进行拉普拉斯分布建模,用最大似然估计计算出一个最优值,然后以这个为目标值,对MLP进行在线训练。
3.3 Mapping and Tracing
Mapping的执行与NICE-SLAM相同,但使用了修正的损失函数:
在优化方面,与NICE-SLAM一样采用了两阶段的方法。对于每个映射阶段,首先对中间网格进行优化,一旦收敛,就包括精细网格进行进一步细化。
这样建模误差函数方法的优势之后会进行说明。
Tracing的执行与NICE-SLAM相同,但使用了修改后的损失函数:
这样建模Tracing的误差函数,可以看到,相比于NICE-SLAM在分母上加上了深度值分布的标准差,相当于考虑了传感器的任意不确定度。
3.4 多传感器深度融合与RGBD融合
假设每个传感器的深度观测都是I.I.D的(独立同分布),我们希望最大化的联合似然是每个传感器中每个像素的概率分布的乘积。给定两个同步对齐的传感器,我们可以对一组像素 m ∈ { 1 , . . . , M } m\in\{1,...,M\} m∈{1,...,M}从两个深度传感器得到广义损失函数:
这个目标函数的一种解释是算法隐式地学习两个传感器观测值之间的权重。损失函数通过对数项惩罚较大的不确定性,并在模型深度优化时隐式学习两组观测值的不确定性。以类似的方式,RGBD融合可以通过损失函数实现:
这种建模不同于NICE-SLAM,其中颜色和几何损失由启发式超参数加权。
笔者的一些理解: 可以看到这个损失函数的前一项,与NICE-SLAM类似,分母部分是标准差,相当于用不确定度进行权重调整,如果不确定度大(标准差大),则这部分不好,相应的权重减小,而不同的是在后面加了一个对数项,通过对数项惩罚较大的不确定性,这样以来,在多传感器融合时,就相当于实现了一个多个传感器之间权重的自学习(精确地传感器权重会大一点),后面也会说明为什么使用的是 β m \beta_m βm而不是NICE-SLAM中的D。
3.5 设计选择和架构细节
按理说,像NICE-SLAM一样,计算出来的方差,可以自然的用于损失函数的计算,在NICE-SLAM中也对这样做的思想进行了说明,很合理,但是这种方法的动机很差,因为计算的方差与模型置信度有关,而不是传感器特定的噪声。作者努力建模的不确定性是偶然不确定性,应该与模型置信度不同;
笔者理解: 作者的意思应该是上面计算的方差是一种模型置信度,随着观测增加,这个不确定性应该减小;而作者寻找一种偶然不确定度,是反映真实观测不确定性的一种置信度,所以不能用方差替代。
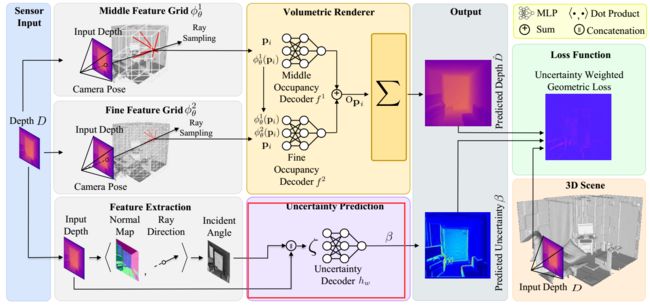
所以作者从Kendall和Gal[29]的工作中获得了隐式学习的偶然不确定性的概念,并设计了一个基于patch(块)的MLP。采用来自特定深度帧的空间信息来生成不确定性前文中的β,与呈现的方差不同且解耦。(这一点在流程图中也可以看到)
作者还考虑到了计算量的问题,由于体绘制是密集的操作,并且每个传感器的额外渲染可能非常昂贵。作者提出了一种更简单的方法,将测量深度 D m D_m Dm和局部射线方向与表面法线之间的入射角 θ θ θ输入MLP。对于RGB不确定性,输入颜色而不是深度和入射角。另外,不是只从单个像素观察中输入特征,而是从5×5的patch中输入特征,有效地扩展了射线的接受域。这一像素块为边缘附近或高频内容的区域提供了局部上下文和不确定性的局部相关性。(笔者理解: 一个边缘(如转角、开着的门)可能有深度差,这些地方可能无法精确计算出入射角,对于这种地方如果联系到了周围的一个patch,就可以对这些区域进行有效计算)
这一过程在流程图中如下所示:
这部分的MLP的由5层每层32个结点的网络组成,使用ReLU函数激活,最后一层采用如下公式进行软激活:
这减轻了优化过程中的数值不稳定性。只在优化的精细阶段更新hw,在中间阶段,使用与NICE-SLAM相同的损失。
4 实验与结果
4.1 单传感器评估
1. Replica数据集
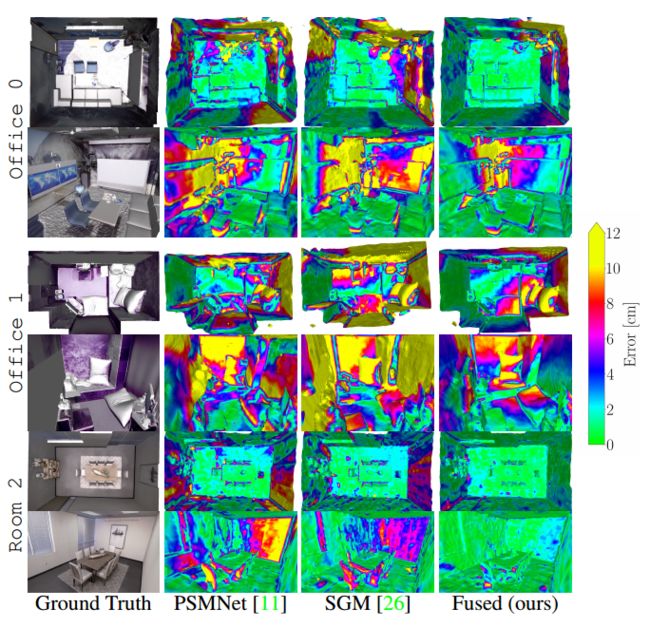
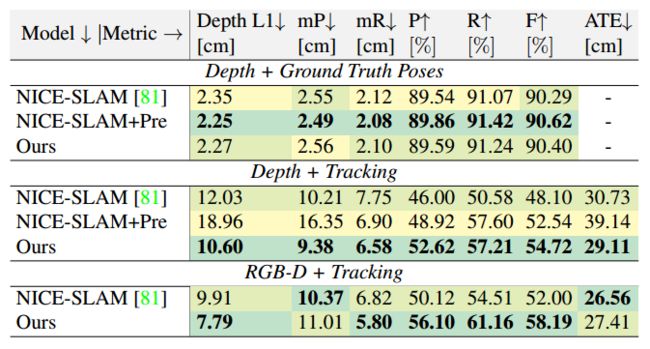
在三种不同的设置下对两种深度传感器(PSMNet(表1)和SGM(表2))进行了实验评估:1.具有地面真值的深度,即噪声深度的纯建图(Mapping);2.深度与估计相机姿势(即带有Tracing)和3.带有Tracing的RGBD。
在图中也可以看到,本文的算法大片区域的不确定度都有效减小。
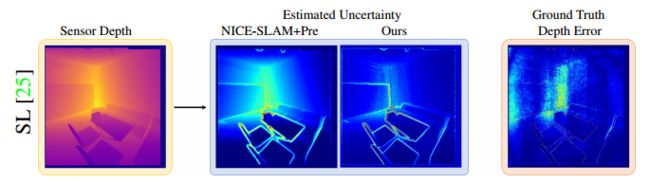
下图可视化了两个深度传感器的估计不确定性,与预训练网络产生的不确定性相比,本文的模型产生了更清晰的估计。
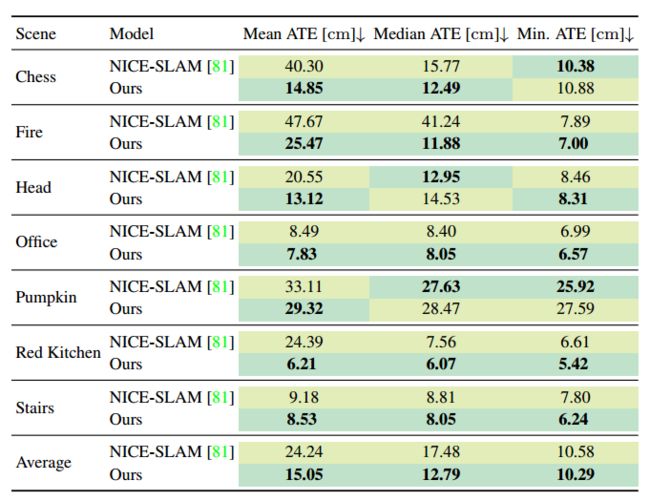
2. 7-Scenes数据集
如下表所示,NICE-SLAM始终产生更差的跟踪结果,这表明提出的深度不确定性在保持稳健的相机姿态跟踪方面是有效的,提出的方法在平均ATE方面产生38%的增益。
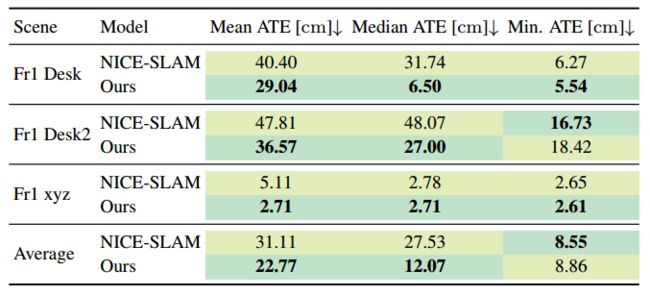
3. TUM-RGBD
得出的结论和7-Scenes相似,如下图,摄像机姿态跟踪很大程度上得益于本文提出的不确定性感知策略。
4.2 多传感器评估
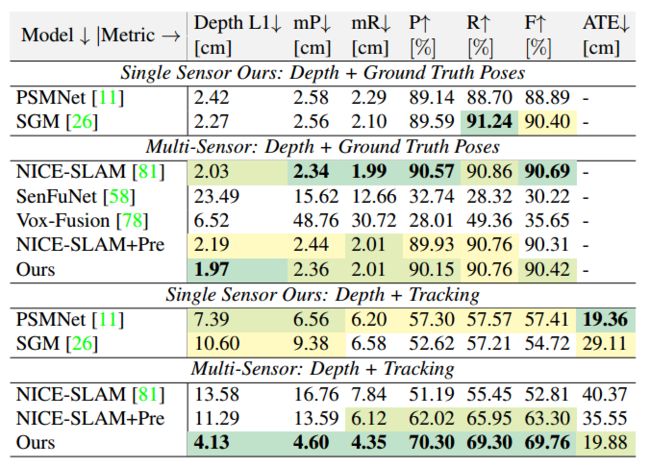
有下图得到:当提供地面真值时,两个传感器得到的结果非常相似(表中第一行),简单的平均工作得很好,即像NICE-SLAM一样对两个传感器施加相同的权重,因此提供地面真值时,NICE-SLAM表现得更好(表中第二行)。
然而,作者发现不确定性建模对于获得鲁棒跟踪非常重要,当加入了Tracing模块时(第三四行),本文的算法展现出了巨大的优势,这大大提高了重建精度。如下图所示。
4.3 内存和运行时间
由于本文的不确定性MLP算法(5409)中的参数数量较少,作者在已经为NICE-SLAM中的解码器分配的421kB的基础上增加了43kB。与为办公室场景的密集网格分配的95.86 MB相比,这是微不足道的。与NICE-SLAM相比,运行时间增加了15%,相比之下,在7-scene和TUM-RGBD数据集上,ATE RMSE的平均增益分别为38%和27%,在单传感器RGBD-SLAM和多传感器深度SLAM上,f1得分分别为11%和32%。
总的来说就是:运行时间和内存有所增加,但定位精度提高更多,性价比更高。
4.4 其他实验
作者做了很多实验,更多详细的实验可以阅读原文的附录。
5 局限性
- 本文的算法使用基于patch的不确定性建模,这可能不适用于一般情况。
- 不确定性解码器使用的特征可能过于廉价、简单。然而,简单地使用一个具有学习特征的更具表现力的模型并不是直截了当的,这样会引入大量的计算量,还是应该考虑是不是能有其他更好的替代特征。
- 最后,比较大的体素尺寸可能会阻碍场景的精细建模,本文的算法可能会受益于更精细的场景表示。