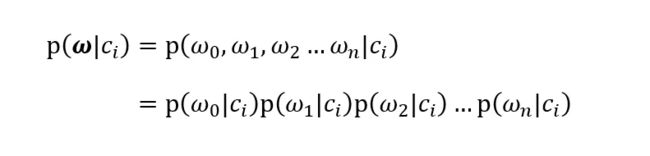机器学习系列_朴素贝叶斯(1)(原理、python代码、实战)
本文经作者允许转载自公众号:月半一更
链接:https://mp.weixin.qq.com/s/v-FN3rG97Hr8Ez_fnkwpTw
前文中的K-近邻、决策树分类器,给出的分类决策都是确定性的,即:该数据实例确定属于哪一类。但是,再好的分类器有时候也会产生错误的分类结果,这时候我们就希望有一个分类器,它能给出一个最优的类别猜测结果,同时也能给出这个猜测的概率估计值。
这种基于分类结果的概率估计值做出最终决策的分类方法,就是朴素贝叶斯分类器。
本篇主要内容:由贝叶斯决策理论开始,阐述基于概率的分类方法的核心思想;然后,我们通过最简单的理论加实例的方式,深入浅出的介绍条件概率及贝叶斯公式,进而引出朴素贝叶斯算法;最后,通过“网站恶意留言过滤系统”的案例,实战代码,并总结和优化。
一 贝叶斯决策理论
朴素贝叶斯是贝叶斯决策理论的一部分,所以在介绍朴素贝叶斯之前,我们首先从全局的高度,去了解贝叶斯决策理论,然后再去钻研算法细节。
假设我们有一个数据集,它由两类数据组成(蓝色数据和青色数据),其数据分布散点图如下。

假设已经通过数据训练出了分类模型,对于新的待分类数据点(x,y),我们用p1(x,y)表示数据点属于类别c1(蓝色)的概率,用p2(x,y)表示数据点属于类别c2(青色)的概率,那么我们可以用下面的规则来判断数据点最终的可能类别:
-
如果p1(x,y) > p2(x,y),那么类别为c1;
-
如果p1(x,y) < p2(x,y),那么类别为c2;
也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
将上面的判定规则,用概率论的语言翻译一下:
-
如果p1(c1 | x,y) > p2(c2 | x,y),那么类别为c1;
-
如果p1(c1 | x,y) < p2(c2 | x,y),那么类别为c2;
其中 p1(c1 | x,y)的具体意义为:**给定某个数据点(x,y),那么该数据点来自类别c1的概率是多少?**p2(c2 | x,y)的意义同理。
到这里,分类的问题,其实就变成了求 p1(c1 | x,y)的概率问题。
那么,p1(c1 | x,y)该怎么求呢?
答曰:条件概率和贝叶斯公式。
二 条件概率
01 什么是条件概率?
02 举个栗子:小球案例
03 联合、边缘、条件概率关系
我们先来看一下什么是条件概率。
例如:有非独立事件A和B,P(A | B)则表示在B事件发生的情况下,A事件也发生的概率。这种某某条件下另一事件发生的概率,就是条件概率。
举个例子:假设现在有一个装有7个球的桶,其中3个球是灰色的,另外4个球是黑色的。如果随机从桶里取出一个球,问该球是黑球的概率是多少?
很容易知道,概率值为4/7,即P(黑) = 4/7。
如果我们将这7个球,分别放到两个桶(A桶和B桶)里,现在随机取出一个球,问该球是黑球的概率是多少?

如果我这样问你,你会说“你疯了吧,你都没告诉我是从哪只桶里取球,我怎么告诉你概率呢?”
是的,在这种情况下,我们想知道所取的球是黑球的概率,就必须知道是从哪只桶取球的。假设球取自B桶,这时球是黑球的概率应该P(黑 | B)表示。
其中:
P(黑 | B) :条件概率。表示,B桶取球条件下,球为黑球的概率。
P(球=黑 ,桶= B):联合概率。表示,球是黑色,同时球来自B桶的概率。由球在桶中的分布可知,球是黑球同时在B桶的个数为2,球总数为7,则联合概率为2/7。
P(桶= B):边缘概率。表示,球来自B桶的概率。
由概率分布表,即可计算出条件概率P(黑 | B),B桶取球条件下,球为黑球的概率为2/3。显然,上帝视角看B桶球的分布,这个概率计算的正确的不能再正确了。

这里顺便讲一下这三者概率之间的关系:
联合概率 P(球=黑 ,桶= B) :同时满足“球是黑球”且“来自B桶”两个条件的球个数(交集),占总球数的比例。基数为全部的球。
边缘概率 P(桶= B):满足“来自B桶”的球个数,占总球数的比例。基数为全部的球。
条件概率 P(黑 | B) :在B桶中,黑球个数占B桶球数的比例。基数为B桶。
最开始学习概率论时候,我最容易混淆的就是联合概率和条件概率。其实只要记住一点,条件概率是有条件才发生的,其基数来自于限定条件。而联合概率和边缘概率,基数都是针对整体全局的。
总结一下前两节:
第一节,我们将分类问题,转化成求取 **p1(c1 | x,y)**的条件概率问题;第二节,我们介绍了条件概率的计算方法。
聪明的你可能发现了,好像有点问题啊!
问题在哪,分析一下:
在机器学习中,拿到一堆标记好类别的训练数据集,我们只能计算出某类别下的各个数据点出现的概率,即p1(x,y | c1),也就是已知某数据点来自c1类,那么该点是(x,y)的概率。
而分类问题中我们需要求的概率是什么?p1(c1 | x,y):是给定数据点(x,y)的条件下,求取该数据点属于类别c1或c2的概率,最终取最高的概率对应的类别作为分类决策。
p1(c1 | x,y)和p1(x,y | c1),那可是大不相同的!
再回到取球的问题上,上面情况下我们要求的是:从B桶取球的条件下,所取的球为黑球的概率。刚才已经计算了,P(黑 | B) = 2/3。
而我们现在问题已经变成了:所取的球为黑球的条件下,问该球来自B桶的概率是多少?即 P(B | 黑)等于多少?
这种交换条件概率中的条件与结果,重新计算概率值,就需要利用强大的贝叶斯公式啦!
三 条件概率与贝叶斯公式
01 条件概率的简单理解
02 贝叶斯公式的简单理解
条件概率、贝叶斯公式的简单理解:
根据文氏图,很显然能够看出P(A|B)表示的是C占B的比例,立即得出条件概率的表达式:
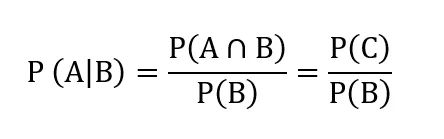
贝叶斯公式,是通过交换条件和结果,利用已知的条件概率去求结果为条件的条件概率,即通过P(A|B),计算P(B|A)。
我们把P(A)称为"先验概率",即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为"后验概率",即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为"可能性函数",这是一个调整因子,使得预估概率更接近真实概率。
这就是贝叶斯公式的含义。我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。
现在,我们回到小球案例:所取的球为黑球的条件下,问该球来自B桶的概率是多少?即 P(B | 黑)等于多少?
这就是贝叶斯公式,通过交换条件概率中的条件与结果,变向求取难以直接计算的条件概率值。即通过P(黑 | B)求P(B | 黑)。
先验概率为3/7,后验概率为1/2,很明显“先验概率”被增强,事件的可能性变大。
这样我们就能回答第二节的问题了,即:可以通过p1(x,y | c1)计算决策分类概率p1(c1 | x,y)。
四 贝叶斯与朴素贝叶斯
01 朴素贝叶斯的条件独立性假设
通过前三节,我们了解了贝叶斯决策理论的核心思想和决策分类的概率计算,并通过条件概率和贝叶斯公式,明确了朴素贝叶斯分类器所需的所有前提知识。
现在只剩下最后一点:朴素贝叶斯条件独立性假设。这也是贝叶斯和朴素贝叶斯的关键区别所在。
为了应用的广泛性,我们重写贝叶斯准则,将之前的x,y替换为ω。粗体ω表示这是一个向量,即它由多个数值组成。因此,决策概率计算公式可由下面公式表示:
朴素贝叶斯条件独立性假设的内容为:假设ω是一个多个独立特征的向量,如果将其展开为一个个独立特征,条件概率公式即可改写成向量中每个特征的概率累乘公式。
贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。
假设某个贝叶斯分类器总共有两类,对于一个新的待分类ω,只需计算P(c1 | ω)和P(c2 | ω),比较其大小即可完成分类。
进一步可以看到,在决策概率计算过程中,分母**P(ω)在P(c1 | ω)和P(c2 | ω)的比较过程中,并没有什么作用。因此,在P(c1 | ω)和P(c2 | ω)**的计算过程中,忽略P(ω)并不影响决策概率的相对大小。
五 小试牛刀:网站恶意留言过滤系统
01 文本拆分、词汇向量
02 词集汇总、数字向量
03 训练模型、概率分类
前四节我们详细介绍了朴素贝叶斯的所有理论知识,说了这么多,最关键的来了:实战!
本节,我们以“网站恶意留言过滤系统”为案例,选取“斑点犬爱好者论坛”的留言板作为数据来源,进行朴素贝叶斯分类模型的训练和测试。
5.1 背景与流程:
为了不影响社区的发展,我们要屏蔽侮辱性的言论,所以要构建一个快速过滤器,如果某条留言使用了负面或者侮辱性的语言,那么就将该留言标志为内容不当。过滤这类内容是一个很常见的需求。对此问题建立两个类型:侮辱类和非侮辱类,使用1和0分别表示。
就本案例而言,从零搭建朴素贝叶斯模型的流程如下:
(1)收集数据:本文数据来自《机器学习实战》。
(2)准备数据:对文本进行词汇拆分,得到词汇向量。
(3)分析数据:汇总词汇,生成词集,并基于词集,将(2)中词汇向量转换为数字向量。
(4)训练算法:计算不同的独立特征的条件概率,根据朴素贝叶斯算法,得出决策概率。
(5)测试算法:利用训练好的分类模型,测试分类的准确度,计算错误率。
(6)使用算法
开始实战之前,为了方便理解,对流程及下文将会出现的关键词作注解:
词汇拆分:对文本中每条留言进行切分,将句子切分为由词汇组成的列表。
留言:“my dog has flea problems help please”
词汇拆分后:['my', 'dog', 'has', 'flea', 'problems', 'help', 'please']
词汇向量:
['my', 'dog', 'has', 'flea', 'problems', 'help', 'please']
词集:所有词汇向量中的词汇汇总,包含训练数据集中出现的所有词汇。
数字向量:基于词集,将词汇向量用数字表示,词汇存在则位置标记为1,否则标记为0,得出数字向量。
词汇向量:['my', 'dog', 'has', 'flea', 'problems', 'help', 'please']
数字向量:[1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1]
5.2 收集数据:message.txt
下图所示“message.txt”中存储的文本内容,即为本案例的数据:六条来自斑点犬爱好者社区留言板的留言。其中每行的第一个字符,为分类标签,1代表侮辱类留言,0代表正常类留言。

5.3 准备数据:词汇切分
读取文件,对文本进行词汇切分,创建留言的词汇向量以及对应的分类标签向量。
# 功能:打开社区留言的txt文件,拆分文本,将每句留言的文本转换成词汇向量
def loadDataSet():
path = r"机器学习message.txt"
dataSet = [] # 文本的词汇向量
label = [] # 文本标签 0:正常言论,1:侮辱性言论
with open(path) as message:
for line in message.readlines():
data_list = line.strip().strip('.').split(' ')
label.append(int(data_list[0]))
dataSet.append(data_list[1:])
return dataSet,label
if __name__ == '__main__':
dataSet, label = loadDataSet()
for each in dataSet:
print(each)
print(label)
输出结果如下,每条留言已经成功被切分为词汇向量,并与分类标签一一对应。
5.4 分析数据:词集、数字向量
汇总训练集中所有的词汇向量,创建“词集”,存储训练数据集中所有出现的词汇。并基于词集,将每条词汇向量转换为数字向量。
对于单条留言的词汇向量,只要在该词汇向量出现过的单词,在词集相应位置标记为1,没有出现过的,则全部标记为0。这样,即可通过0、1两个数字的向量组合,表示词汇向量所包含的词汇。数字向量的意义即在于此。
# 功能:打开社区留言的txt文件,拆分文本,将每句留言的文本转换成词汇向量
# dataSet:词汇向量
# label:文本标签
def loadDataSet():
path = r"C:Usersyong_Desktop机器学习message.txt"
dataSet = [] # 文本的词汇向量
label = [] # 文本标签 0:正常言论,1:侮辱性言论
with open(path) as message:
for line in message.readlines():
data_list = line.strip().strip('.').split(' ')
label.append(int(data_list[0]))
dataSet.append(data_list[1:])
return dataSet,label
# 功能:创建训练数据集的所有不重复词汇的列表,包含留言板文本中所有单词
# vocabSet:词汇集
def createVocabList(dataSet):
vocabSet = set([]) #创建一个空的集合
for message in dataSet:
vocabSet = vocabSet | set(message) #取并集
return list(vocabSet)
# 功能:基于词汇集,将词汇向量转换成数字向量
# vocabList:词汇集
# inputSet:每条词汇向量
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0] * len(vocabList) #创建一个其中所含元素都为0的向量
for word in inputSet: #遍历每个词汇
if word in vocabList: #如果词汇存在于词汇集中,则置1
returnVec[vocabList.index(word)] = 1
else: print("the word: %s is not in my Vocabulary!" % word)
return returnVec #返回单条词汇向量的数字向量
if __name__ == '__main__':
dataSet, label = loadDataSet() # 01 词汇切分,生成每句留言的词汇向量
total_VocabList = createVocabList(dataset) # 02 词汇汇总,生成总的词汇集,包括训练数据集中所有出现过的词汇
trainMat = [] # 03 将每条词汇向量,转换成数字向量
for one_message in dataSet:
digital_list = setOfWords2Vec(total_VocabList,one_message)
trainMat.append(digital_list)
print("训练数据集的数字向量:{}".format(trainMat))
print("数字向量对应的分类标签:{}".format(label))
如上述代码,增加了两个方法(createVocabList、setOfWords2Vec),其中createVocabList方法是用来创建词集,setOfWords2Vec方法是将词汇向量转为数字向量。
5.5 训练模型:利用数字向量计算概率
前面我们已经得到训练数据集中每条的留言的数字向量,本节需要做的就是建立和训练分类模型。
训练分类模型,说白了,就是**计算每个类别中各特征的概率,再由朴素贝叶斯公式,计算分类决策概率。**这里的类别只有两类:侮辱类、正常类,特征指的就是某类留言拆分后的每个词汇。
# 01 功能:打开社区留言的txt文件,拆分文本,将每句留言的文本转换成词汇向量
# dataSet:词汇向量
# label:文本标签
def loadDataSet():
path = r"C:Usersyong_Desktop机器学习message.txt"
dataSet = [] # 文本的词汇向量
label = [] # 文本标签 0:正常言论,1:侮辱性言论
with open(path) as message:
for line in message.readlines():
data_list = line.strip().strip('.').split(' ')
label.append(int(data_list[0]))
dataSet.append(data_list[1:])
return dataSet,label
# 02 功能:创建训练数据集的所有不重复词汇的列表,包含留言板文本中所有单词
# vocabSet:词汇集
def createVocabList(dataSet):
vocabSet = set([]) #创建一个空的集合
for message in dataSet:
vocabSet = vocabSet | set(message) #取并集
return list(vocabSet)
# 03 功能:基于词汇集,将词汇向量转换成数字向量
# vocabList:词汇集
# inputSet:每条词汇向量
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0] * len(vocabList) #创建一个其中所含元素都为0的向量
for word in inputSet: #遍历每个词汇
if word in vocabList: #如果词汇存在于词汇集中,则置1
returnVec[vocabList.index(word)] = 1
else: print("the word: %s is not in my Vocabulary!" % word)
return returnVec #返回单条词汇向量的数字向量
# 04 功能:利用数字向量训练朴素贝叶斯分类器
# trainMatrix:词条的数字向量
# trainCategory:label,词条的分类标签
def train_NB(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix) # 训练集的留言条数
numWords = len(trainMatrix[0]) # 词集中词汇总数
pAbusive = sum(trainCategory)/float(numTrainDocs) # 侮辱类留言占训练集的比例
p0Num = np.zeros(numWords); p1Num = np.zeros(numWords) #创建numpy.zeros数组,词汇出现数初始化为0
p0Denom = 0.0; p1Denom = 0.0 #分母初始化为0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
# 统计侮辱类留言中每个单词出现的频率向量
p1Num += trainMatrix[i]
# 统计被训练的侮辱类留言中所有的词汇数,包括重复出现的词汇
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
# 频率/类别总词数,即为侮辱类里某单词出现的概率,同理计算非侮辱类
p1Vect = p1Num/p1Denom
p0Vect = p0Num/p0Denom
return p0Vect,p1Vect,pAbusive #返回属于侮辱类的条件概率数组,属于非侮辱类的条件概率数组,文档属于侮辱类的概率
# 05 朴素贝叶斯分类器分类函数
# vec2Classify - 待分类的词条数组
# p0Vec - 侮辱类的条件概率数组
# p1Vec -非侮辱类的条件概率数组
# pClass1 - 文档属于侮辱类的概率
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
pClass0 = 1.0 - pClass1
p1 = reduce(lambda x,y:x*y, vec2Classify * p1Vec) * pClass1 #对应元素相乘
p0 = reduce(lambda x,y:x*y, vec2Classify * p0Vec) * pClass0
print('p0:',p0)
print('p1:',p1)
if p1 > p0:
return 1
else:
return 0
# 功能:获取数据、切分数据、向量转换、训练模型
def start():
dataSet, label = loadDataSet() # 01 词汇切分,生成每句留言的词汇向量
total_VocabList = createVocabList(dataset) # 02 词汇汇总,生成总的词汇集,包括训练数据集中所有出现过的词汇
trainMat = [] # 03 将每条词汇向量,转换成数字向量
for one_message in dataSet:
digital_list = setOfWords2Vec(total_VocabList,one_message)
trainMat.append(digital_list)
p0_vect,p1_vect,pAbu = train_NB(trainMat,label) # 04 训练分类器
# 功能:测试分类器模型
def test_NB():
test_message1 = ['love', 'my', 'dalmatian'] # 测试样本1
test_vect1 = np.array(setOfWords2Vec(total_VocabList, test_message1)) # 测试样本数字向量化
if classifyNB(test_vect,p0_vect,p1_vect,pAbu): # 06 分类测试
print(test_message1,'属于侮辱类')
else:
print(test_message1,'属于非侮辱类')
test_message2 = ['stupid', 'garbage'] # 测试样本1
test_vect2 = np.array(setOfWords2Vec(total_VocabList, test_message2)) # 测试样本数字向量化
if classifyNB(test_vect,p0_vect,p1_vect,pAbu): # 06 分类测试
print(test_message2,'属于侮辱类')
else:
print(test_message2,'属于非侮辱类')
if __name__ == '__main__':
start()
test_NB()
上述代码,增加了四个函数,但是关键函数只有train_NB和classifyNB,train_NB方法用于训练分类模型,得出两个类别下各特征的概率向量;classifyNB方法根据朴素贝叶斯算法,计算分类的决策概率。两个方法共同成为“朴素贝叶斯分类器模型”。
test_NB方法中,分别用两个测试例子,测试算法的准确性。
然而,训练了这么久的分类器,处女秀就失败了!!如下框图所示,错误分类了侮辱类词条,且并未输出p0和p1两个类别概率值。
问题出在哪儿呢?
六 存在的问题及改进
01 零值概率问题
利用贝叶斯分类器对留言进行分类时,要计算多个概率的乘积以获得留言属于某个类别的概率,即计算:
p(w0|1)p(w1|1)p(w2|1)…p(wn|1)
如果其中有一个概率值为0,那么最后的成绩也为0,这时分类器显然不具有分类作用。
因此,我们的朴素贝叶斯分类器,还需要进行改进。怎么进行改进呢?
且待下文分解~
参考文献:
[1] Peter Harrington. 机器学习实战[M]. 2013.
[2] https://cuijiahua.com/blog/2017/11/ml_4_bayes_1.html(Jack Cui)
[3] 平冈和幸,崛玄. 程序员的数学2[M].
[4] 李航.统计学习方法[M].北京:清华大学出版社,2012
[5] 小岛宽之. 统计学关我什么事[M]. 北京时代华文书局, 2018.
[6] 维基百科