机器学习-神经网络-手写数字识别-KNN（有代码，有解析，有数据集，可视化）

机器学习-神经网络-手写数字识别

（注：本篇文章仅用于学习人工智能时的一些个人笔记，有错误请指出）
问题描述： 手写数字识别是指给定一系列的手写数字图片以及对应的数字标签，构建模型进行学习，目标是对于一张新的手写数字图片能够自动识别出对应的数字。这里主要涉及到的技术是图像识别， 图像识别是指利用计算机对图像进行处理、分析和理解，以识别各种不同模式的目标和对像的技术。机器学习领域一般将此类识别问题转化为多分类问题。
环境搭建：pycharm，jupyter.
jupyter notebook是一种超轻量级的交互式的编辑器用来数据分析十分方便。

引入：神经网络是机器学习中十分重要的一个算法，也是作为深度学习的入门算法之一，因此至关重要，我们在此将神经网络与KNN实现的手写数字识别，做一个对比。

1.数据收集与可视化

本实验采取的数据来自kaggle(一个数字识别的比赛网站，可以提交计算正确率)，共有42000个训练集，28000个测试集，如果网站有注册问题登录不上去，文末提供一个答案仅供参考，数据集也在文末给出。

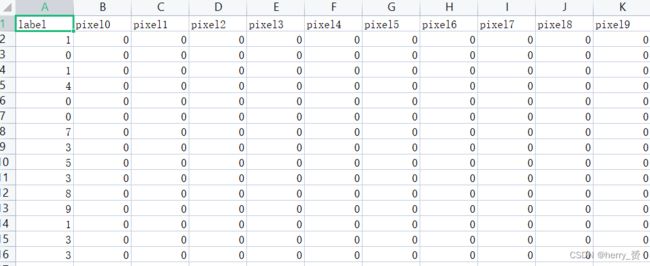
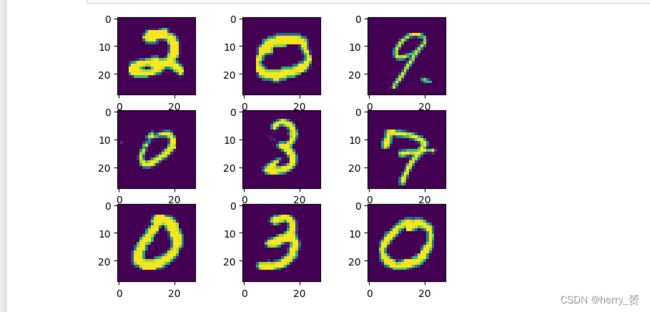
每行数据由785个单元促成，第一列是标签，后面784列是一个平铺的28*28的图片像素值，像素值如上，如果是将其可视化，需要转换为28**28的一个矩阵才可。用python处理完后结果类似下图

for i in range(9):
    plt.subplot(3,3,i+1)
    plt.imshow(data1.iloc[i,1:].values.reshape(28,28))

下面以两个算法为例实现手写数字的识别。

2.KNN 实现手写数字识别

KNN的基础不在此赘述，此文主要讲神经网络实现。

2.1.数据收集

在上一部分已经阐述。

2.2. 数据处理

KNN算法的测试集和训练集全部来自train这个文件里面，每次随机选取了80%作为测试集，20%作为训练集。

import pandas as pd  # 导入pandas库
start_time = time.time() # 时间计算函数，用来记录处理时间
data = pd.read_csv('F:\S\\train.csv') 
#读入csv数据文件 如果加了 header = None 可能会有类型错误
m = 0.8   #测试机和训练集的划分比例
n = int(data.shape[0]*m)  #训练集的个数
#随机打乱并且重新设置索引
data_1 = data.sample(frac=1).reset_index(drop=True) 
#切分数据集 分为训练集和测试集
train = data_1.iloc[:n,:]
test = data_1.iloc[n:,:].reset_index(drop=True)

read_csv 和read_table 都是pandas库所带的读取表格的方法。
data.sample 是指随机打乱顺序。
reset_index是指重新分配索引从0开始（打乱后索引会混乱）

2.3.模型构建与预测

选取适当的k值进行模型预测（不同K值的准确率不相同）

k = 4 # 设置分类
result = [] # 通过knn分类得到的标签
for i in range(test.shape[0]):
    # 算出来每个测试的元素距离所有训练集元素的距离
    dist = list(((train.iloc[:,1:]-test.iloc[i,1:])**2).sum(1)**0.5)
    # 将距离和标签设置成为dataframe格式 方便下面处理
    dist_1 = pd.DataFrame({'dist':dist,'labels':(train.iloc[:,0])})
    # 找到k值内出现最多的标签即为该测试集的预测结果
    dr = dist_1.sort_values(by='dist')[:k]
    # 讲dist排序从小到大排序，找到距离最近的k个点
    re = dr.loc[:,'labels'].value_counts()
    # 从距离最近的k个点找到出现最多的标签就是该分类值
    result.append(re.index[0])
test['predict']=result # 将预测的标签放入原测试集中进行对比
print(test)

主要就是用pandas进行处理方便数据计算和准确率计算。

2.4准确率分析

用.mean（）来算取准确率的平均值。

acc = (test.iloc[:,-1]==test.iloc[:,0]).mean()
# 求出来预测的准确率
end_time = time.time()
run_time = end_time-start_time
print(acc)
print(end_time-start_time)

[8400 rows x 786 columns]   
0.9689285714285715   #  准确率
2185.26634144783       #  耗时

从上述数据中可以看出，KNN 的准确率不超过97%

2.5.优缺点分析

由time（）计算出来的时间可以看出，KNN对42000个数据的训练和测试的计算时间已经达到了2185s即36min不止（可能是我没有独显，但是确实也挺慢的）所以我们需要开发出来一种更优化的计算模型来进行处理这个图像识别的问题。

3.神经网络（基于tensorflow）实现数字识别

3.1. 基础算法知识

神经元和多层感知器
单个神经元：就如下图右上角的部分，神经元在工作时，将前一层神经元的输出与权重w相乘再加上一个偏移量bias得到的结果，传递给下一层神经元。

多层感知器：（人工神经网络）是指含有至少一个隐藏层的由全连接层组成的神经网络，其中每一个隐藏层的输出都会通过激活函数进行变换。多层感知机的层数、隐藏层的大小、激活函数都是超参数，可以自己设定。

神经网络的基本原理是：每个神经元把最初的输入值乘以一定的权重，并加上其他输入到这个神经元里的值（并结合其他信息值），最后算出一个总和，再经过神经元的偏差调整，最后用激励函数把输出值标准化。基本上，神经网络是由一层一层的不同的计算单位连接起来的。我们把计算单位称为神经元，这些网络可以把数据处理分类，就是我们要的输出。

与其他模型求解问题一样，训练神经网络，是一个最优化问题，即找到让模型效果最好的哪些参数。为了解决这个问题，传统算法有的通过数学解析计算理论最优，有的通过启发式算法搜索效果最好。神经网络的做法，是前向传播和反向传递的组合。

前向传播，是将输入值（观测值）经过一层层的计算（包括线性计算和非线性激活）得到输出值的预测值的过程。算法开始之前，线性计算的参数W和b都是随机给出，因此预测值与真实值之间差异很大。通俗的来讲就是从左到右计算结果的过程

反向传播，是根据预测值与真实值之间的差异，调整模型参数W和b。为了保证调整参数的方向是减小这一差异，这里用到了梯度下降的原理。通俗的来讲，就是根据误差调节参数的过程

介绍这个梯度下降算法之前先提及一下线性回归模型，例如初中所学最小二乘估计f(x) = ax + b
寻求一个合适的参数a和b使得对应不同的y值算出来更加与真实值接近，
从而达到一个更好的预测效果。其实就是寻找一个合适的a和b来使得
(f(x)-y)^2 / n   也就是(均方差)最小，这里就要用到梯度下降算法了。

梯度下降算法是一种致力于找到函数极值点的算法。所谓"学习”便是改进模型参数，以便通过大量训练步骤将损失最小化。有了这个概念，将梯度下降法应用于寻找损失函数的极值点便构成了依据输入数据的模型学习
应用最小二乘估计的例子就是下图，自变量为a和b，z即损失函数红色线几位梯度下降最快的方向，因此可以在梯度下降的方向不断调整a，b的大小使得损失函数z逐渐减小达到最优，注意神经网络里面不用考虑局部极值点问题。
图片

如图在红色方向是梯度下降最快的方向，因此调整下面两个坐标即参数a,b的值来使得损失函数不断下降，在神经网络中adam也是用的这个方法的升级版进行调参。

在神经网络中，激活函数的作用是能够给神经网络加入一些非线性因素（如果不使用激活函数，神经网络中的每一层的输出只是承接了上一层输入函数的线性变换，无论神经网络有多少层，输出都是输入的线性组合），使得神经网络能够很好的解决比较复杂的问题。比如手写数字识别（10分类问题）用到的softmax函数，逻辑回归用到的sigmod函数。

tf.keras搭建神经网络可以参考的七步法
·第一步：import相关模块，如import tensorflow as tf，pandas，matplotlib等
·第二步：指定输入网络的训练集和测试集，如指定训练集的输入x_train和标签y_train，测试集的输入x_test和标签y_test，可以进行可视化。
·第三步：逐层搭建网络结构，model=tf.keras.model.Sequential()。
·第四步：在model.compile()中配置训练方法，选择训练时使用的优化器、损失函数和最终评价指标。
·第五步：在model.fit()中执行训练过程，告知训练集和测试集的输入值和标签、每个batch的大小（batchsize）和数据集的迭代次数（epoch）。
·第六步：使用model.summary()打印网络结构，统计参数数目。
·第七步：使用pandas.to_csv or to_table 存储结果

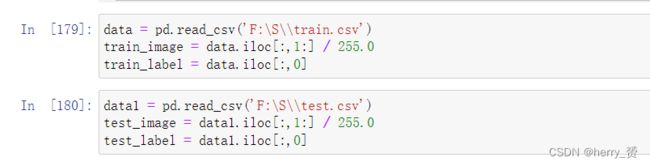
3.2. 数据预处理

首先肯定是导入包啦！

然后将两个文件的数据分别读入数据集和测试集以及相对应的image和label
并进行归一化处理（归一化可以提高的模型的准确度和收敛速度）
简单的归一化处理就是直接除以最大值255，也有其他的方法如min-max归一化和Z-score标准化等。

3.3.模型构建

此处借助tensorflow搭建神经网络：

（1）Sequential

Sequential函数是一个容器，描述了神经网络的网络结构，在Sequential函数的输入参数中描述从输入层到输出层的网络结构。
拉直层：

tf.keras.layers.Flatten()  
拉直层可以变换张量得到尺寸，把输入特征拉直为一维数组，是不含计算参数的层

全连接层：

tf.keras.layers.Dense（ 神经元个数，activation='激活函数',
						kernel_regularizer='正则化方式') 
# 其中：activation（字符串给出）可选relu、softmax、sigmoid、tanh等

卷积层：tf.keras.layers.Conv2D(filter=卷积核个数， kernel_size=卷积核尺寸， strides=卷积步长， padding=‘valid’ or ‘same’)

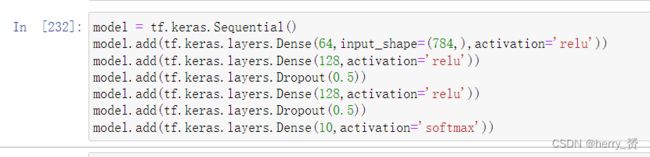
Dropout层 用来解决过拟合问题，训练时随机丢弃一些神经元，但在测试的时候又重新使用。

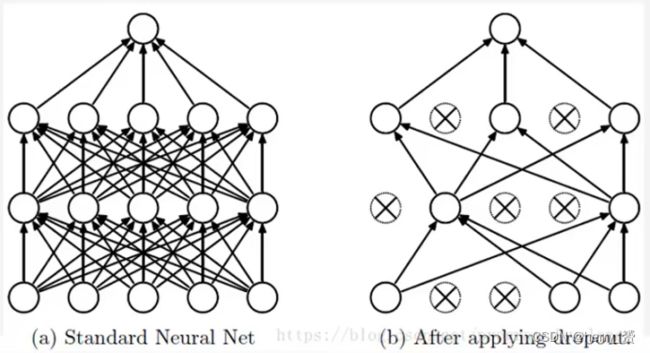
为什么说Dropout可以解决过拟合?
减少神经元之间复杂的共适应关系:因为dropout程序导致两个神经元不一定每次都在一 个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用，阻止了某些特征仅仅在其它特定特征下才有效果的情况。

（2）Model.compile( optimizer=优化器， loss=损失函数，metrics=[‘acc’]）

Model.compile( optimizer=优化器， loss=损失函数，metrics=[‘acc’]）
Compile用于配置神经网络的训练方法，告知训练时使用的优化器、损失函数和准确率评测标准。
这里优化器采取adam也就是梯度下降算法实现，optimizer可以是字符串给出的优化器名字，也可以是函数形式，使用函数形式可以自己设置学习率、动量和超参数，但是一般学习速率设置为0.001，如果过快会导致模型不准确。
Metrics标注网络评测指标。

损失函数多分类主要应用以下两种。

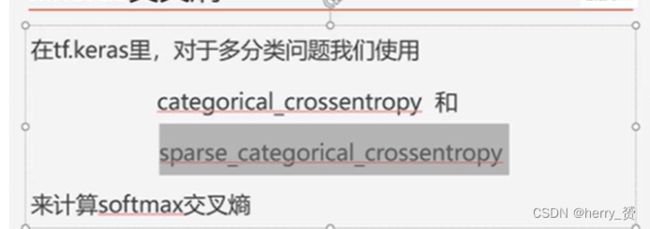
第一个是独热编码（one-Hot），结果是一个含有十个概率的列表，第二个是顺序数字编码，结果是自然数。

（3）训练模型model.fit()

model.fit(训练集的输入特征，训练集的标签，
	batch_size=每次喂入神经网络的样本数，
	epochs=数据集迭代次数，
	validataion_data=（测试集的输入特征，测试集的标签），
	validataion_split=从测试集划分多少比例给训练集，
	validataion_freq=测试的epoch间隔次数)）

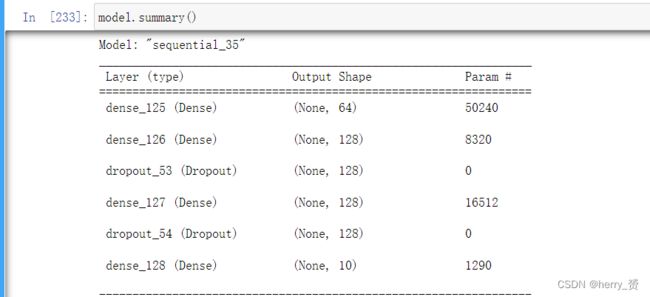
（4）summary函数用于打印网络结构和参数统计

summary函数用于打印网络结构和参数统计
如果只采用了三个神经元，对于一个四输入三输出的全连接网络，共有15个参数
因为四输入就是四个权重参数加一个偏移常数 一共五个参数再乘以三输出一共十五个参数， 手写数字识别参数个数也可以类比

（5）model.predict

( x（输入样本）,batch_size=None（批量大小）,verbose=0（是否显示进度条）)
model.evaluate（x,y,batch_size=?）同样也可以进行测试并且可以直接算出准确率。


下图是一个训练准确率和测试准确率的一个对比。结合拟合情况，可进一步分析。

（6）如果有想要存到文件里的可以采用下列pandas方法。

3.4.对比分析

从运行时间上很明显的就可以看出来，运行速率大大提高，准确率也有所提升，如果要想把正确率再次提高，可以借助CNN卷积神经网络。后续会继续探讨。

3.5.细节

如何选取超参数？

所谓超参数，也就是搭建神经网络中，需要我们自己选择(不是通过梯度下降算法去优化)的那些参数。比如，中间层的神经元个数、学习速率。

参数选择的一些原则

1.首先开发一个过拟合的模型:(1)添加更多的层。(2)让每一层变得更大。(3)训练更多的轮次
2.然后抑制过拟合：（1）dropout（2）正则化（3）图像增强

4.完整代码

KNN实现

#todo  KNN实现手写数字分类
import pandas as pd  # 导入pandas库
import time
start_time = time.time()
data = pd.read_csv('F:\S\\train.csv') #读入csv数据文件 如果加了header = None 可能会有类型错误
m = 0.8  #测试机和训练集的划分比例
n = int(data.shape[0]*m) #训练集的个数
data_1 = data.sample(frac=1).reset_index(drop=True) #随机打乱并且重新设置索引
#切分数据集
train = data_1.iloc[:n,:]
test = data_1.iloc[n:,:].reset_index(drop=True)
# for i in range(785):
#     test.iloc[:,i] = pd.to_numeric(test.iloc[:,i],errors='ignore')
print(data_1)
k = 4 # 设置分类
result = [] # 通过knn分类得到的标签
for i in range(test.shape[0]):
    # 算出来每个测试的元素距离所有训练集元素的距离
    dist = list(((train.iloc[:,1:]-test.iloc[i,1:])**2).sum(1)**0.5)
    # 将距离和标签设置成为dataframe格式 方便下面处理
    dist_1 = pd.DataFrame({'dist':dist,'labels':(train.iloc[:,0])})
    # 找到k值内出现最多的标签即为该测试集的预测结果
    dr = dist_1.sort_values(by='dist')[:k]
    re = dr.loc[:,'labels'].value_counts()
    result.append(re.index[0])
test['predict']=result # 将预测的标签放入原测试集中进行对比
print(test)
acc = (test.iloc[:,-1]==test.iloc[:,0]).mean()
# 求出来预测的准确率
print(acc)
end_time = time.time()
run_time = end_time-start_time
print(end_time-start_time)

神经网络实现

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

data = pd.read_csv('F:\S\\train.csv')
train_image = data.iloc[:,1:] / 255.0
train_label = data.iloc[:,0]

data1 = pd.read_csv('F:\S\\test.csv')
test_image = data1.iloc[:,1:] / 255.0
test_label = data1.iloc[:,0]

model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(64,input_shape=(784,),activation='relu'))
model.add(tf.keras.layers.Dense(128,activation='relu'))
model.add(tf.keras.layers.Dropout(0.2))
model.add(tf.keras.layers.Dense(128,activation='relu'))
model.add(tf.keras.layers.Dropout(0.2))
model.add(tf.keras.layers.Dense(10,activation='softmax'))

model.summary()

model.compile(optimizer='adam',
              loss = 'sparse_categorical_crossentropy',
              metrics = ['acc']
)
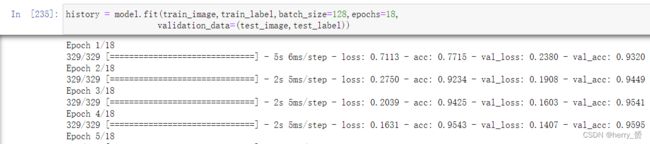
history = model.fit(train_image,train_label,batch_size=128,epochs=18,
                   validation_data=(test_image,test_label))

plt.plot(history.epoch,history.history.get('acc'),label='acc')
plt.plot(history.epoch,history.history.get('val_acc'),label='val_acc')
plt.legend()

model.evaluate(test_image,test_label,batch_size=1)
# 可视化
for i in range(9):
    plt.subplot(3,3,i+1)
    plt.imshow(data1.iloc[i,1:].values.reshape(28,28))

# 文件存储
result_dig = pd.DataFrame({"ImageId":index1,
             "Label":result1})
result_dig.to_csv('F:\S\\result.csv')

数据集评论区回复，私发你奥！！
参考文献：
http://t.csdn.cn/cQaAi
http://t.csdn.cn/H4w0t
https://blog.csdn.net/Dream_Gao1989/article/details/110708484