【贪心】单源最短路径Python实现
文章目录
-
- @[toc]
-
- 问题描述
- `Dijkstra`算法
- `Dijkstra`算法的正确性
-
- 贪心选择性质
- 最优子结构性质
- `Dijkstra`算法应用示例
- 时间复杂性
- `Python`实现
文章目录
-
- @[toc]
-
- 问题描述
- `Dijkstra`算法
- `Dijkstra`算法的正确性
-
- 贪心选择性质
- 最优子结构性质
- `Dijkstra`算法应用示例
- 时间复杂性
- `Python`实现
![]()
个人主页:丷从心
系列专栏:贪心算法
![]()
问题描述
- 给定一个带权有向图 G = ( V , E ) G = (V , E) G=(V,E),其中每条边的权是非负实数,给定 V V V中的一个顶点,称为源
- 计算从源到所有其他各顶点的最短路长度
Dijkstra算法
Dijkstra算法是解单源最短路径问题的一个贪心算法- 其基本思想是,设置顶点集合 S S S,并不断地做贪心选择来扩充这个集合,一个顶点属于集合 S S S当且仅当从源到该顶点的最短路径长度已知
- 初始时, S S S中仅含有源,设 u u u是 G G G的某一个顶点,把从源到 u u u且中间只经过 S S S中顶点的路称为从源到 u u u的特殊路径,并用数组
dist记录当前每个顶点所对应的最短特殊路径长度,用列表parent[i]记录从源到顶点 i i i的最短路径上 i i i的前一个顶点 Dijkstra算法每次从 V − S V - S V−S中取出具有最短特殊路长度的顶点 u u u,将 u u u添加到 S S S中,同时对列表dist和parent做必要的修改,当dist[u] + graph[u][i] < dist[i]时,置dist[i] = dist[u] + graph[u][i],置parent[i] = u- 一旦 S S S包含了所有 V V V中顶点,
dist就记录了从源到所有其他顶点之间的最短路径长度
Dijkstra算法的正确性
贪心选择性质
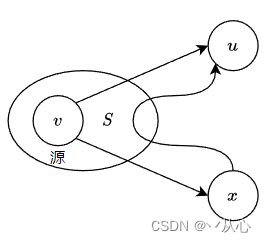
Dijkstra算法所做的贪心选择是从 V − S V - S V−S中选择具有最短特殊路径的顶点 u u u,从而确定从源到 u u u的最短路径长度dist[u],从源到 u u u没有更短的其他路径- 事实上,如果存在一条从源到 u u u且长度比
dist[u]更短的路,设这条路初次走出 S S S之外到达的顶点为 x ∈ V − S x \in V - S x∈V−S,然后徘徊于 S S S内外若干次,最后离开 S S S到达 u u u
- 在这条路径上,分别记 d ( v , x ) d(v , x) d(v,x)、 d ( x , u ) d(x , u) d(x,u)和 d ( v , u ) d(v , u) d(v,u)为顶点 v v v到顶点 x x x、顶点 x x x到顶点 u u u和顶点 v v v到顶点 u u u的路长,那么
dist[x]≤ d ( v , x ) \leq d(v , x) ≤d(v,x), d ( v , x ) + d ( x , u ) = d ( v , u ) < d i s t [ u ] d(v , x) + d(x , u) = d(v , u) < dist[u] d(v,x)+d(x,u)=d(v,u)<dist[u],利用边权的非负性,可知 d ( x , u ) ≥ 0 d(x , u) \geq 0 d(x,u)≥0,从而推得dist[x]< < <dist[u],此为矛盾 - 这就证明了
dist[u]是从源到顶点 u u u的最短路径长度
最优子结构性质
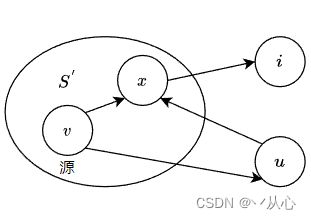
- 将添加 u u u之前的 S S S称为 S ′ S^{'} S′
- 当添加了 u u u后,可能出现一条到顶点 i i i的新的特殊路
- 如果这条新特殊路是经过 S ′ S^{'} S′到达顶点 u u u,然后从 u u u经一条边直接到达顶点 i i i,则这种路的最短的长度是
dist[u]+ + +c[u][i],此时,如果dist[u]+ + +c[u][i]< < <dist[i],则算法中用dist[u]+ + +c[u][i]作为dist[i]的新值 - 如果这条新特殊路经过 S ′ S^{'} S′到达 u u u后,不是从 u u u经一条边直接到达 i i i,而是回到 S ′ S^{'} S′中某个顶点 x x x,最后才到达顶点 i i i,那么由于 x x x在 S ′ S^{'} S′中,因此 x x x比 u u u先加入 S S S,故从源到 x x x的路的长度比从源到 u u u,再从 u u u到 x x x的路的长度小,于是当前
dist[i]的值小于这条新特殊路的长度,因此,在算法中不必考虑这种路 - 由此可知,不论算法中
dist[u]的值是否有变化,它总是关于当前顶点集 S S S到顶点 u u u的最短特殊路径长度
Dijkstra算法应用示例
- 对下图中的有向图,应用
Dijkstra算法计算从源顶点 1 1 1到其他顶点间最短路径的过程如下表所示
| 迭代 | S S S | u u u | dist[2] |
dist[3] |
dist[4] |
dist[5] |
|---|---|---|---|---|---|---|
| 初始 | { 1 } \set{1} {1} | − - − | 10 10 10 | m a x i n t maxint maxint | 30 30 30 | 100 100 100 |
| 1 1 1 | { 1 , 2 } \set{1 , 2} {1,2} | 2 2 2 | 10 10 10 | 60 60 60 | 30 30 30 | 100 100 100 |
| 2 2 2 | { 1 , 2 , 3 } \set{1 , 2 , 3} {1,2,3} | 4 4 4 | 10 10 10 | 50 50 50 | 30 30 30 | 90 90 90 |
| 3 3 3 | { 1 , 2 , 4 , 3 } \set{1 , 2 , 4 , 3} {1,2,4,3} | 3 3 3 | 10 10 10 | 50 50 50 | 30 30 30 | 60 60 60 |
| 4 4 4 | { 1 , 2 , 4 , 3 , 5 } \set{1 , 2 , 4 , 3 , 5} {1,2,4,3,5} | 5 5 5 | 10 10 10 | 50 50 50 | 30 30 30 | 60 60 60 |
时间复杂性
- 对于一个具有 n n n个顶点的带权有向图,
Dijkstra算法进行二重循环,需要 O ( n 2 ) O(n^{2}) O(n2)时间
Python实现
import sys
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for _ in range(vertices)] for _ in range(vertices)]
def printSolution(self, dist, parent):
for v in range(self.V):
path = []
curr = v
while curr != -1:
path.append(curr)
curr = parent[curr]
path.reverse()
print((v, dist[v], path))
def minDistance(self, dist, sptSet):
min_value = sys.maxsize
min_index = -1
for v in range(self.V):
if dist[v] < min_value and not sptSet[v]:
min_value = dist[v]
min_index = v
return min_index
def dijkstra(self, src):
dist = [sys.maxsize] * self.V
dist[src] = 0
sptSet = [False] * self.V
parent = [-1] * self.V
for _ in range(self.V):
u = self.minDistance(dist, sptSet)
sptSet[u] = True
for v in range(self.V):
if self.graph[u][v] != 0 and 0 < dist[u] + self.graph[u][v] < dist[v] and not sptSet[v]:
dist[v] = dist[u] + self.graph[u][v]
parent[v] = u
self.printSolution(dist, parent)
g = Graph(9)
g.graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],
[4, 0, 8, 0, 0, 0, 0, 11, 0],
[0, 8, 0, 7, 0, 4, 0, 0, 2],
[0, 0, 7, 0, 9, 14, 0, 0, 0],
[0, 0, 0, 9, 0, 10, 0, 0, 0],
[0, 0, 4, 14, 10, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 1, 6],
[8, 11, 0, 0, 0, 0, 1, 0, 7],
[0, 0, 2, 0, 0, 0, 6, 7, 0]]
src = 0
print(f'(顶点, 以顶点 {src} 为源的最短路径长度, 最短路径)')
print('-' * 40)
g.dijkstra(src)
print('-' * 40)
(顶点, 以顶点 0 为源的最短路径长度, 最短路径)
----------------------------------------
(0, 0, [0])
(1, 4, [0, 1])
(2, 12, [0, 1, 2])
(3, 19, [0, 1, 2, 3])
(4, 21, [0, 7, 6, 5, 4])
(5, 11, [0, 7, 6, 5])
(6, 9, [0, 7, 6])
(7, 8, [0, 7])
(8, 14, [0, 1, 2, 8])
----------------------------------------