机器学习——KNN案例

【说明】文章内容来自《机器学习——基于sklearn》，用于学习记录。若有争议联系删除。

1、电影类型

        电影类型根据搞笑镜头、拥抱镜头、打斗镜头的数量分为喜剧片、爱情片、动作片等，如图所示。现有电影《唐人街探案》，其搞笑镜头为23个，拥抱镜头为3个，打斗镜头为17个，预测该电影的类型。

序号	电影名称	搞笑镜头	拥抱镜头	打斗镜头	电影类型
1	《宝贝当家》	45	2	9	喜剧片
2	《美人鱼》	21	17	5	喜剧片
3	《澳门风云3》	39	0	31	喜剧片
4	《功夫熊猫3》	39	0	31	喜剧片
5	《谍影重重》	5	2	57	动作片
6	《叶问3》	3	2	65	动作片
7	《伦敦陷落》	2	3	55	动作片
8	《我的特工爷爷》	6	4	21	动作片
9	《奔爱》	7	46	4	爱情片
10	《夜孔雀》	9	39	8	爱情片
11	《代理情人》	9	38	2	爱情片
12	《新步步惊心》	8	34	17	爱情片

代码：

import math
movie_data = {'《宝贝当家》': [45, 2, 9, '喜剧片'],
             '《美人鱼》':[21, 17, 5, '喜剧片'],
             '《澳门风云3》':[54, 9, 11, '喜剧片'],
             '《功夫熊猫3》':[39, 0, 31, '喜剧片'],
             '《谍影重重》':[5, 2, 57, '动作片'],
             '《叶问3》':[3, 2, 65, '动作片'],
             '《伦敦陷落》':[2, 3, 55, '动作片'],
             '《我的特工爷爷》':[6, 4, 21, '动作片'],
             '《奔爱》':[7, 46, 4, '爱情片'],
             '《夜孔雀》':[3, 2, 65, '爱情片'],
             '《代理情人》':[9, 38, 2, '爱情片'],
             '《新步步惊心》':[8, 34, 17, '爱情片'],}
#测试样本：'《唐人街探案》':[23,3,17,'?']
x = [23, 3, 17]
KNN = []
#采用欧几里德距离
for key, v in movie_data.items():
    d = math.sqrt((x[0] - v[0]) ** 2 + (x[1] -v[1])** 2 + (x[2]-v[2])**2)
    KNN.append([key, round(d,2)])
#输出所有电影到《唐人街探案》的距离
print("《唐人街探案》到各个影片的距离如下：\n")
print(KNN)
#按照距离递增排序
KNN.sort(key = lambda dis: dis[1])
#选取距离最小的k个样本，这里取k=5
KNN = KNN[:5]
print('距离最小的前5部影片如下:')
print((KNN))
#确定前K个样本所在类别出现的频率，并输出频率最高的类别
labels = {'喜剧片':0,'动作片':0,'爱情片':0}
for s in KNN:
    label = movie_data[s[0]]
    labels[label[3]] +=1
labels = sorted(labels.items(), key = lambda l:l[1], reverse = True)
print(labels)
print('《唐人街探案》所属影片类型如下：')
print(labels[0][0])

【运行结果】

2、鸢尾花

用KNN算法进行鸢尾花识别

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
#步骤1:通过datasets加载鸢尾花数据集
iris = datasets.load_iris()#鸢尾花数据集包含4个特征变量
#步骤2：划分数据集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=6)
#步骤3：特征工程（标准化）
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
#步骤4：KNN算法预估器
estimator = KNeighborsClassifier(n_neighbors = 3)
estimator.fit(x_train, y_train)
#步骤5：模型评估采用如下两种方法
#方法1：直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print(y_predict)
print('比对真实值和预测值:\n', y_test == y_predict)
#方法2：计算准确率
score = estimator.score(x_test, y_test)
print('准确率:\n', score)

【运行结果】

3、波士顿房价

import pandas as pd
import numpy as np

data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]

print(data.shape)
x = data
y = target
from sklearn.feature_selection import SelectKBest, f_regression
#筛选和标签最相关的5个特征
# SelectKBest 类会计算每个特征的评分，然后根据评分选择最好的 k 个特征。
# 评分函数是 f_regression，这个函数使用 F 检验来计算特征的相关性。
selector = SelectKBest(f_regression, k = 5)
x_new = selector.fit_transform(x,y)
print('最相关的5列是:\n', selector.get_support(indices = True).tolist())
#将索引值存储在indices变量中没然后转换为list

from sklearn.model_selection import train_test_split
#划分数据集
x_train, x_test, y_train, y_test = train_test_split(x_new, y, test_size = 0.3,
                                                    random_state = 666)
from sklearn.preprocessing import StandardScaler
#均值方差归一化
standardscaler = StandardScaler()
standardscaler.fit(x_train)
x_train_std = standardscaler.transform(x_train)#标准差
x_test_std = standardscaler.transform(x_test)

from sklearn.neighbors import KNeighborsRegressor
#训练
KNN_reg = KNeighborsRegressor()
KNN_reg.fit(x_train_std, y_train)
#预测
y_pred = KNN_reg.predict(x_test_std)

from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
print(np.sqrt(mean_squared_error(y_test, y_pred)))#计算均方差根判断效果
print(r2_score(y_test, y_pred))#计算均方误差回归损失，越接近1，拟合效果越好

import numpy as np
import matplotlib.pyplot as plt
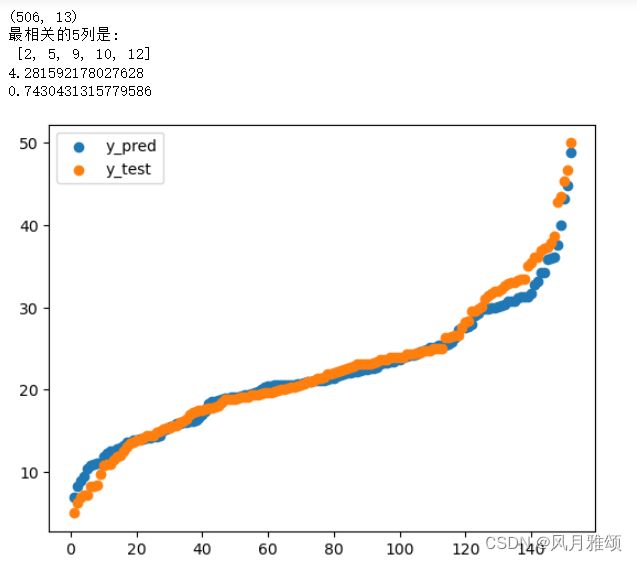
#绘图展示预测效果
y_pred.sort()
y_test.sort()
x = np.arange(1,153)
Pplot = plt.scatter(x, y_pred)
Tplot = plt.scatter(x, y_test)
plt.legend(handles = [Pplot, Tplot], labels = ['y_pred', 'y_test'])
plt.show()

【运行结果】

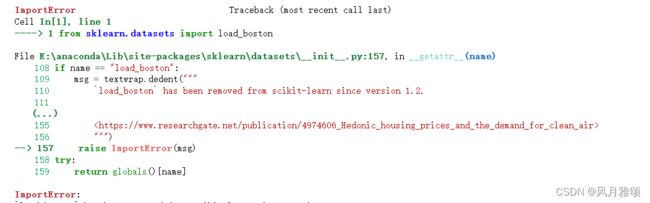
【说明】引入波士顿房价问题：from sklearn.datasets import load_boston调用的时候出现问题，

错误提示为：

原因，sklearn1.2版本后波士顿房价数据移除。

修改为：

import pandas as pd
import numpy as np
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]

可以调用波士顿房价数据使用。

4、印第安人的糖尿病

数据链接：https://pan.baidu.com/s/1aPekKeiQA7qRcyNYiL_jGw 
提取码：gpt4

import pandas as pd
data = pd.read_csv('diabetes.csv')
print('dataset shape {}'.format(data.shape))
data.info()

【运行结果】

【结果分析】

印第安人的糖尿病数据集总共有768个样本、8个特征。其中,Outcome为标签，是示没有糖尿病，1表示有糖尿病。8个特征如下:

• Pregnancies:怀孕次数。
• Glucose:血浆葡萄糖浓度，采用两小时口服葡萄糖耐量实验测得。
• BloodPressure:舒张压，
• SkinThickness:肱三头肌皮肤褶皱厚度，
• Insulin:两小时血清胰岛素。
• BMI:身体质量指数,体重除以身高的平方。
• Diabetes Pedigree Function:糖尿病血统指数。糖尿病和家庭遗传相关。
• Age:年龄。

print(data.head())

【运行结果】

x = data.iloc[:, 0:8]
y = data.iloc[:, 8]
print('shape of x{}, shape of y {}'.format(x.shape, y.shape))
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2)

【运行结果】

#构建3个模型，分别对数据集进行拟合并计算评分
from sklearn.neighbors import KNeighborsClassifier, RadiusNeighborsClassifier
models = []
#普通的KNN算法
models.append(('KNN', KNeighborsClassifier(n_neighbors = 2)))
#带权重的KNN算法
models.append(('KNN with weights', KNeighborsClassifier(n_neighbors = 2, weights = 'distance')))
#指定半径的KNN算法
models.append(('Radius Neighbors',RadiusNeighborsClassifier(radius=500.0)))#限定半径最近邻分类树

#分别训练以上3个模型，并计算得分
results = []
for name, model in models:
    model.fit(x_train, y_train)
    results.append((name, model.score(x_test, y_test)))
for i in range(len(results)):
    print('name:{}; score:{}'.format(results[i][0], results[i][1]))

【运行结果】

【结果分析】

        从输出可以看出，普通KNN算法最好，但是，由于训练集和测试集是随机分配的，不同的训练样本和测试样本组合可能导致算法准确性差异，从而导致判断不准确。采用多次随机分配训练集和交叉验证集，求模型评分的平均值的方法进行优化，Sklearn提供了FKold(k折交叉验证)和cross_val_score函数处理。

from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
 
results=[]
for name,model in models:
    kfold=KFold(n_splits=10)
    cv_result=cross_val_score(model,x,y,cv=kfold)
    results.append((name,cv_result))
for i in range(len(results)):
    print("name:{},cross_val_score:{}".format(results[i][0],results[i][1].mean()))

【运行结果】

#使用普通的KNN算法模型，查看对训练样本的拟合情况及测试样本的预测准确性
knn = KNeighborsClassifier(n_neighbors = 2)
knn.fit(x_train, y_train)
train_score = knn.score(x_train, y_train)
test_score = knn.score(x_test, y_test)
print('train score:{};test score:{}'.format(train_score, test_score))

【运行结果】

from sklearn.model_selection import learning_curve
#画学习曲线，可以直接返回训练样本、训练集分数、测试集分数
import numpy as np
def plot_learning_curve(plt, estimator, title, x, y, ylim = None, cv = None, n_jobs = 1,
                       train_sizes = np.linspace(.1, 1.0, 5)):
    plt.title(title)
    if ylim is not None:
        plt.ylim(* ylim)
    plt.xlabel('training examples')
    plt.ylabel('score')
    train_size, train_scores, test_scores = learning_curve(estimator, x, y, cv = cv,
                                                         n_jobs = n_jobs, train_sizes = train_sizes)
    train_scores_mean = np.mean(train_scores, axis = 1)
    train_scores_std = np.std(train_scores, axis = 1)
    test_scores_mean = np.mean(test_scores, axis = 1)
    test_scores_std = np.std(test_scores, axis = 1)
    plt.grid()
    plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
                    train_scores_mean + train_scores_std, alpha = 0.1, color = 'r')
    plt.fill_between(train_size, test_scores_mean - test_scores_std,
                    test_scores_mean + test_scores_std, alpha = 0.1, color = 'g')
    plt.plot(train_sizes, test_scores_mean, 'o--', color = 'r',label = 'Training score')
    plt.plot(train_sizes, test_scores_mean, 'o--', color = 'g',
            label = 'Cross-validation score')
    plt.legend(loc = 'best')
    return plt
from sklearn.model_selection import ShuffleSplit
import matplotlib.pyplot as plt
knn = KNeighborsClassifier(n_neighbors = 2)
cv = ShuffleSplit(n_splits = 10, test_size = 0.2, random_state = 0)
plt.figure(figsize = (6,4), dpi = 200)
plot_learning_curve(plt, knn, 'learn Curve for KNN Diabetes', x, y, ylim = (0.0, 1.01), 
                    cv=cv)

【运行结果】