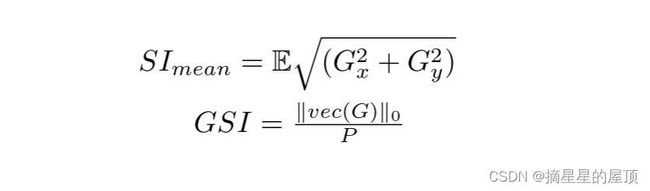论文学习记录之OpenFWI（Large-scale Multi-structuralBenchmark Datasets for Full Waveform Inversion）
目录
0 Abstract—摘要
1 Introduction—简介
2 Seismic FWI and Forward Modeling—地震FWI和正演模拟
3 OpenFWI Datasets and Domain Interests—OpenFWI数据集与领域兴趣
4 OpenFWI Benchmarks—OpenFWI基准
4.1 Deep Learning Methods for FWI—FWI的深度学习方法
4.2 Inversion Benchmarks—反演基准
4.2.1 2D FWI Benchmarks—2D FWI基准
4.2.2 3D FWI Benchmarks—3D FWI基准
5 消融研究
5.1 Velocity Map Complexity Analysis—速度图复杂性分析
5.2 Generalization Study—泛性研究
5.3 Uncertainty Quantification—不确定性量化
5.4 Additional Experiments—另外的实验
6 讨论
6.1 Future Challenges—未来挑战
6.2 Broader Impact—更广泛的影响
7 结论
附录安排：
A OPENFWI Public Resources and Licenses
B Velocity Map Generation（未完）
C Seismic Forward Modeling Details（未完）
D OPENFWI Datasets: Illustration, Format, Naming, Loading—OpenFWI数据集：插图、格式、排版与加载（未完）
E OPENFWI Benchmarks: Network Architecture（待理解与修改）
E.1 InversionNet
E.2 VelocityGAN
E.3 UPFWI（代理解）
E.4 InversionNet 3D
F OPENFWI Benchmarks: Training Configurations—OpenFWI基准：训练配置
G Illustration of Inversion Results—反演结果演示
H Velocity Map Complexity—速度图复杂度
I Generalization Test
J Uncertainty Quantification—不确定性度量
K Robustness Test（未完）
L Comparison with Physics-driven Methods（未完）
M Comparison between InversionNet and InversionNet3D—InversionNet和InversionNet 3D的比较（未完）
N Test Strategy in Real-world Situation（未完）
O Passive Picking
P Discussion
P.1 Past Version—过去版本
P.2 Limitations—限制
9 常用关键术语
10 思考
- Title：OPENFWI: Large-scale Multi-structural Benchmark Datasets for Full Waveform Inversion
- 标题：基于全波形反演的大规模多结构基准数据集
- 36th Conference on Neural Information Processing Systems (NeurIPS 2022) Track on Datasets and Benchmarks.
arXiv:2111.02926v6 [cs.LG] 24 Jun 2023
0 Abstract—摘要
全波形反演（FWI）是地球物理学中广泛应用的一种从地震资料中重建高分辨率速度图片的方法。最近速度驱动的FWI方法的成功导致对服务于地球物理学社区的开放数据集的需求迅速增加。由此，提出了OpenFWI数据集——一个大规模的多结构基准数据集，以促进FWI的多样化、严格化和可重复性的研究。特别是，OpenFWI由多个来源合成的12个数据集（共2.1TB）组成。它包括地球物理学的不同领域（界面、断层、二氧化碳储层等），覆盖不同的地质地下结构（平坦、弯曲等），并且也包含了各种数量的数据样本（2K~67K）。它还包括一个三维的FWI数据集。此外，本文使用OpenFWI对四种深度学习的方法进行基准测试，涵盖监督与无监督学习机制。沿着基准测试，本文还进行了额外的实验，包括物理驱动方法、复杂性分析、泛化研究、不确定性量化等，以加深我们对数据集和方法的理解。
所有的数据集和相关信息（包括代码）可以通过网站访问：Open FWI | A collection of benchmark datasets for Seismic FWI with Machine Learning
1 Introduction—简介
了解速度结构对无数的地下应用至关重要，比如碳封存、储层识别、地下能源勘探、地震预警等。它们可以通过全波形反演（FWI）从地震数据中重建，这是由偏微分方程（PDEs）控制的，并且它们可以被公式化为非凸优化问题。FWI在物理驱动方法的范例中被深入研究。这些方法的负面复杂性包括高计算消耗、跳过周期和不适定性问题。
随着深度学习技术的进步，研究人员一直在积极探索复杂的FWI问题的数据驱动解决方案。最近，数据驱动的方法见证了对FWI的探索，特别是在网络架构上，例如多层感知器（MLP）、基于编码器-解码器的卷积神经网络（CNNs）、递归网络、生成对抗性网络（GANs）等，将数据驱动的FWI从2D扩展到3D。UPFWI利用控制声波方程将学习范式从监督转为无监督，它提供了关于纯粹基于深度学习的FWI的详细调查，并对物理指导的数据驱动的FWI方法进行了全面概述。
数据是数据驱动方法的氧气，公开数据集在开发尖端机器学习算法中占据重要的位置。然而，FWI社区目前缺乏大型公共数据集。现有的地震数据集[34，35，18，17，36，37]尚未向公众发布。因此，很难在不同方法之间进行公平的比较。
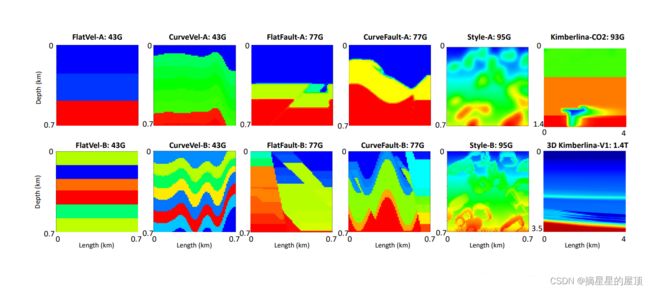
在这里，本文基于我们的知识，提出了OpenFWI—第一个大规模的开放获取多结构地震FWI数据集。它包含12个数据集，每个数据集将地震数据与不同的地下结构速度图进行配对。速度图示例如图1所示。OpenFWI数据集与其他现有的数据驱动FWI数据集之间的比较如表1所示。与以前的数据集相比较，OpenFWI的数据集是开源的，涵盖2D和3D场景，在多个尺度上捕获更多的地质结构。
图1：OpenFWI图库，其中包含OpenFWI中每个数据集的速度图示例。
表一：数据驱动FWI的现有数据集（最上面的一行对应于的OpenFWI数据集。符号√和×分别指示数据集具有或不具有对应特征。）
OpenFWI数据集具有以下有利特征：
- 多尺度：OpenFWI涵盖了多尺度的数据集，包括数据样本的数量和文件大小。最小的2D数据集有15K个数据样本，而最大的2D数据集包含60K个样本。其中四个2D数据集每个占用43GB的空间，这支持在没有大量计算能力的情况下进行训练。3D数据集占用1.4TB的空间，因此通常在分布式环境中进行训练，进一步加快了基于深度学习的FWI的可扩展算法的开发。
- 多领域：OpenFWI支持FWI的2D和3D场景研究。数据集包括真实地下应用的速度图，例如延时成像、地下碳汇、地质断层探测等。
- 多地下复杂性：OpenFWI包括从简单到复杂的各种地下结构，如界面、断层、二氧化碳存储和自然图像中的自然结构。复杂性主要由香农熵来衡量。它支持研究人员从适度的速度集开始，并改进他们的方法以适应更具有挑战性的数据集。
OpenFWI允许在多个数据集熵对不同的方法进行公平比较。本文在2D数据集上评估了三种代表性方法（InversionNet [20]，VelocityGAN [27]和UPFWI [31]），并在3D Kimberlina-V1数据集上评估了InversionNet 3D [30]。本文希望这些结果可以为未来的工作提供一个基线。有关再现性的尝试，请参阅补充材料第1节中列出的资源以及许可证。
OpenFWI还促进了其他相关的研究，如复杂性分析、不确定性量化、泛化等。限于篇幅，本文简要总结了这些研究的结果，并在补充材料中提供了详细信息。特别是，良好的泛化性被认为是数据驱动FWI的一个重要特性，作为一种乌托邦式的方法，被期望学习反演的物理规则，因此在使用看不见的数据进行测试的时候会引起小的误差。然而，本文的实证研究表明：现有方法在泛化性方面遭受了不可忽略的退化，这是与目标数据集的地下结构的复杂性有关。
本文其余部分的组织结构如下：第二部分介绍FWI的物理背景；第三部分介绍了领域兴趣关注的数据集特性；第四部分简要介绍了四种用于基准测试的深度学习方法，并展示了每个数据集的反演性能；第六部分，讨论了地下结构的复杂性、泛化性和不确定性量化，然后展望未来的挑战；最后，第七部分对全文进行了总结。
2 Seismic FWI and Forward Modeling—地震FWI和正演模拟
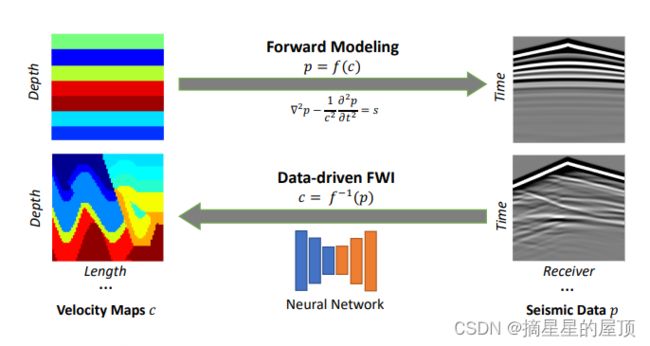
图2提供了2D数据驱动的FWI方法以及速度图与其中的地震数据之间的关系简明图示。在具有恒定密度的各项同性介质中的声波正演模拟的控制方程如下：
（1）
上式中，
，c表示速度图，p表示压力场，s表示震源项。速度图c取决于空间位置（x,y,z），而压力场p和震源项s取决于空间位置和时间（x,y,z,t）。在研究中，本文专注于受控源方法，因此震源项s是确定的。声波传播的正演模拟需要再给定速度c的情况下通过等式1计算压力场p。简单起见，将正演模拟的问题的表达式表示为
，其中
表示高度非线性前向映射。数据驱动的FWI利用神经网络学习逆映射：
图2：数据驱动的FWI和正演建模示意图（神经网络用于从地震数据中推断速度图，正演模拟使用提供的速度图利用波动方程计算地震数据。）
3 OpenFWI Datasets and Domain Interests—OpenFWI数据集与领域兴趣
OpenFWI数据集包含不同的地下结构，涵盖多个领域，因此支持由物理学领域兴趣所激发的研究。表2和表3总结了OpenFWI中所有数据集的基本信息和物理意义，其中包括11个2D数据集和1个3DFWI数据集。
表2：数据总结（数据大小说明如下：速度图如下-深度×宽度×长度；地震数据表示-震源数×时间×宽度上的接收器数量×长度上的接收器数量）
表3：OpenFWI数据集的物理意义
数据集分为四组：“Vel”、“Fault”、“Style”、“Kimberlina”，以解决以下五个潜在的话题。根据地下结构的复杂性，前三个系列包含两个版本：简单（A）和困难（B）。关于数据集复杂性度量的详细信息可以在第5.1节中找到。
OpenFWI数据集支持的领域兴趣包括：
- 描述地下结构并限制岩层速度特性的界面。为了检测界面，“Vel”提供了由具有清晰界面的平坦和弯曲层组成的速度图。在A版本中，层内速度值随深度逐渐增大，而在B版本中，层内速度值呈随机分布。
- 由移动的岩层引起的断层可以捕获流体烃并形成储层。断层探测对于识别、表征和定位储层至关重要。“Fault”包括由速度图中的断层引起的不连续性，这使得能够识别断层。版本B比版本A表现出更多的不连续性和更快的速度变化。
- 不同测区的野外数据具有很高的多样性和复杂性，对反演精度具有很大的影响。“Style”通过从多样化的自然图像中生成速度图来丰富数据集的多样性，这使得在一般情况下可以反演野外数据。版本B具有高分辨率速度图，而版本A中的速度图需要通过高斯滤波器进行平滑，并且相应的地震数据包含的事件较少。
- 二氧化碳储存，通过将二氧化碳注入储层进行长期存储，是实现大气层二氧化碳排放量显著减少的最有前途的方法之一。“Kimberlina”由两个通过地质碳封存（GCS-地质固碳）存储高保真度模拟的数据集。“Kimberlina-CO2”描述了储层内超临界二氧化碳羽流的空间和时间迁移，并附有200年时间范围内的时间戳，可用于二氧化碳存储问题，比如泄漏检测和测量。
- 自[43]以来，随着3D勘探的广泛实施，3D地震技术越来越受到关注。“3D Kimberlina-V1”数据集是第一个大规模的公共3DFWI数据集。它由多个机构[44]生成，并在美国能源部（DOE）-SMART计划[45]下得到支持。它是为开发此类技术（不限于FWI）而设计和指定的。它包含大量的高分辨率三维速度图和地震数据。
值得注意的是，速度图是从三个来源生成的：数学函数、自然图像和地质储层。这一特性显著增强了速度图的多样性和通用性。补充材料的第2节和第3节分别详细阐述了速度图和地震数据生成管道的细节。此外，在补充材料的第4节提供了有关数据格式、加载和所有必要信息的详细说明。
4 OpenFWI Benchmarks—OpenFWI基准
4.1 Deep Learning Methods for FWI—FWI的深度学习方法
我们介绍了四种基于深度学习的方法，2D FWI的InversionNet、VelocityGAN和UPFWI，以及3D FWI的InversionNet，并报告反演结果作为初始基准。如上所述，UPFWI是一种无监督学习方法，而其余的都属于经典的监督学习机制。我们分别提供了每种方法的总结如下：
- InversionNet[20]提出了一种全卷积网络来模拟地震反演过程。通过编码器-解码器，以多个源的二维（时间×接收器数量）地震数据作为输入，预测二维（深度×长度）速度图作为输出，在监督方案中训练网络。
- VelocityGAN[27]采用基于GAN的网络模型来解决FWI。生成器是一个编码器-解码器结构，其性能类似于InversionNet，而卷积神经网络是一个CNN，旨在对真实的和虚拟的速度图进行分类。它进一步使用基于网络的深度迁移学习来提高模型的鲁棒性和泛化能力。
- UPFWI31]将正演模拟和CNN连接在一个循环中，以实现无监督学习，而无须地面真实速度图进行训练。通过CNN从地震数据预测速度图，然后将其馈送到可微分正演模型中以重建地震数据。最后，通过计算输入地震数据和重建数据之间的损失来闭合环路。
- InversionNet 3D[30]将InversionNet扩展到3D领域。为了减少内存占用并提高计算效率（即，3D反演中最具有挑战性的两个障碍），该网络在编码器中利用群卷积，并通过基于加法耦合的可逆层采用部分可逆架构[46]。
4.2 Inversion Benchmarks—反演基准
本节演示基线结果。我们在表4中展示了三种2D深度学习方法的性能，在表6中分别展示了3D FWI的InversionNet3D。这些方法的网络架构和超参数在补充材料的第5节中提供。我们考虑三个指标：平均绝对误差（MAE）、均方根误差（RMSE）和结构相似性（SSIM）[47]。MAE和RMSE都捕获了预测速度图和真实速度图之间的数值差异。SSIM测量两个图像之间的感知相似性。
表4：2D FWI数据集上三种基准测试方法的定量结果。
表5：OpenFWI数据集上每个基准测试的训练时间。注意，UPFWI和InversionNet 3D的训练时间占用了32个GPU，其余的使用的单个GPU。
4.2.1 2D FWI Benchmarks—2D FWI基准
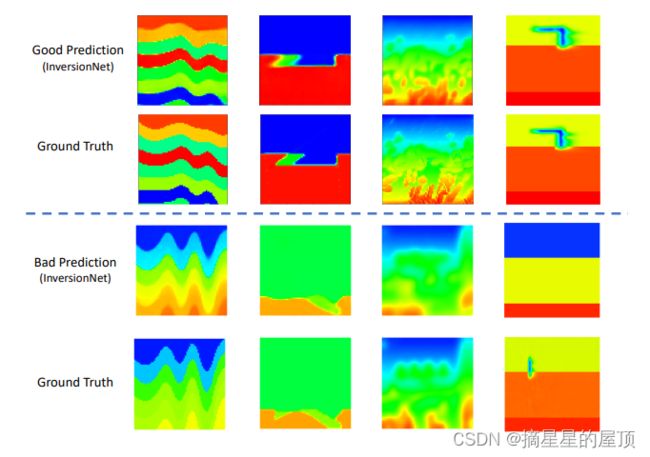
所有2D数据集的训练参数都是相同的，并且在使用Kimberlina-CO2数据集进行训练时，模型架构仅略有变化，这注意其数据具有不同的输入和输出形状。两个最常用的损失函数L1-norm和L2-norm，被用作InversionNet和VelocityGAN中的度量，而UPFWI使用L1-norm、L2-norm和混合损失的组合[31]。所有的实验都在NVIDIA Tesla P100 GPU上实现。表4显示了所有2D数据集上三种模型的反演性能，表5显示了OpenFWI数据集上每种方法的预估训练时间。请注意：UPFWI没有在Kimberlina-CO2上进行评估，因为它的计算成本很高。图3中展现了反演速度图和地面真实情况反应，其中我们显示了成功的反演结果和不太有希望的结果。有关训练配置和更多反演结果的详细信息，请分别参见补充材料的第6节和第7节。
从表4中，我们观察到所有三种方法在简单数据集（如FlatVel-A和FlatFault-A）上都表现良好。然而，在困难数据集（CurveFault-B，Style-B等）上存在相当大的改进空间。值得注意的是，VelocityGAN在大多数数据集上的表现都优于InversionNet，并且在其余数据集上显示出相当的结果。值得一提的是，VelocityGAN需要更多的训练时间才能获得比InversionNet更好的结果。由于地震数据中的频带有限，UPFWI速度图的性能在很小程度上低于监督方法。CurveFault-B的显著性能下降表明需要对UPFWI方法进行额外的改进。
图3：前两行：通过InversionNet和地面真实情况对四个数据集（从左到右）进行良好预测的速度图的说明：CurveVel-B，FlatFault-A，Style-B和Kimberlina-CO2。最后两行：InversionNet和地面真实情况对四个数据集（从左到右）的错误预测速度图的说明：CurveVel-A，FlatFault-A，Style-A和Kimberlina-CO2。
4.2.2 3D FWI Benchmarks—3D FWI基准
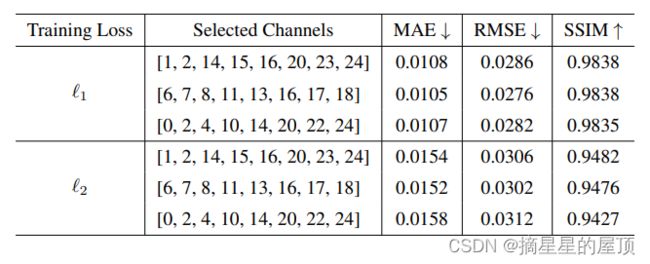
Kimberlina 3D-V1是最近生成的实验数据集，仅报告了InversionNet 3D的性能。在表6中，我们包括了InversionNet 3Dx1（网络的最浅版本）在三通道分布上的性能，其中一个是随机选择的，另外两个是对称的。图4说明了地震数据中的25个震源（道）的序列号分配。与L1损失相比，L2损失导致SSIM 3%的退化。更多的细节和分析可以在[30]中找到。
图4：源的空间放置。每个震源是一个道的输入地震数据。
表6：InversionNet 3D在3D Kimberlina-V1数据集上使用不同地震输入通道选择策略的定量结果。
5 消融研究
5.1 Velocity Map Complexity Analysis—速度图复杂性分析
回想一下，速度生成的第一步是合成来自不同先验的速度图，模拟各种地质地下结构（界面、层、断层等）。因此，速度图包括包含不同程度的复杂性。我们采用三个标准度量：香农熵、空间信息和梯度稀疏指数来比较所有2D数据集的相对模型复杂度。空间信息捕获平均边界幅度，并且梯度稀疏指数测量非平滑像素的百分比。他们的数学公式在补充材料的第8节中给出，其中还包括数值结构和插图。
我们的目标是探索地下地质和性能之间的联系。因此，在8个数据集中的“Vel”和“Fault”上，我们展现了他们的关系与三个复杂性指标以及SSIM的三个二维基准方法。选择这两个系列的原因是它们遵循相同的生成策略。从线性回归获得的散点图和折线图可以在图5中找到，其指示反演性能与速度图复杂性呈负相关，这与表4中的数值结果相对应。这个结论并不让人惊讶，因为直觉很简单：从地震数据中反演复杂的速度图应该更困难。
图5：从左到右：三个复杂度指标（空间信息、梯度稀疏指数、香农熵）与SSIM。三种2D基准方法（InversionNet、VelocityGAN和UPFWI）分别以蓝色、橙色和绿色着色。蓝线是从平均SSIM的线性回归中获得的。
5.2 Generalization Study—泛性研究
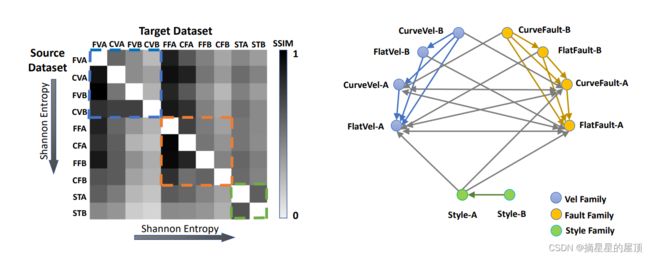
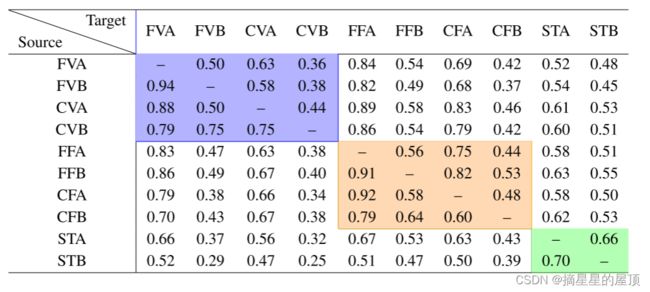
我们在“Vel”、“Fault”和“Style”系列中的10个数据集上进行成对泛化测试。具体来说，我们通过VelocityGAN在每个数据集上选择训练的最好模型（[27]声称它显示出必InversionNet更好的泛化结果），并使用其余的9个数据集进行了测试。泛化性能是通过SSIM度量来衡量的，我们的得到了10×10的矩阵，如图6的热力图所示，颜色越深表示泛化效果越好。我们基于泛化性能提取这10个数据集之间的关系，如图6右侧所示。结果分析在两个方面：域内和跨域。
- 域内：关注热力图图6上的3个对角块（每个数据家族用不同颜色的虚线矩形包围），我们观察到下三角形条目的值总是大于上三角形中的值，这意味着从较难的数据集到较容易的数据集的泛化比其他方式更有希望。
- 跨域：当元数据集固定时，随着复杂性的增加，目标数据集的泛化会下降。从图中，我们还观察到具有“A”的数据集上的节点的度总是高于具有“B”的数据集。样式B的数据集在与其他系列中的数据集没有传入边或者传出边，因此可以被视为一个具有挑战性的泛化数据集。更多关于泛化研究的讨论见补充材料第9节。
图6：热力图（左）和泛化性能图（右）。“FVA”是“FlatVelA”的缩写，其余数据集也是如此。箭头“X—>Y”表示在X上训练并在Y上测试的模型，其SSIM度量高于0.6。
5.3 Uncertainty Quantification—不确定性量化
我们在CurveVel—A上进行实验，对InversionNet中的不确定性进行了量化实验。如图7所示，边界的不确定性高于其他区域，这意味着边界周围的预测更加敏感。我们还观察到随着噪音水平的增加，不确定性也增加。此外，交叉数据集的不确定性明显高于在统一数据集上进行训练和测试，这表明域偏移会导致不确定性增加。实现详情和更多的结果见补充材料第10节。
图7：不确定性可视化。与其他区域相比，边界上的不确定性更高。
5.4 Additional Experiments—另外的实验
我们进行了更多的实验，包括鲁棒性测试、物理驱动方法和数据驱动方法之间的比较，InversionNet和InversionNet3D之间的比较以及真实场景中为目标选择数据集的演示。上述所有内容都是数据驱动的FWI社区的主要关注点。由于篇幅限制，我们简要介绍了这些实验的结果，更多细节分别在补充材料的第11、12、13和14节中提供。
- 鲁棒性测试：模型在2D干净的数据集上训练，但在多个噪声级别的含噪地震数据上进行测试。毫不奇怪，随着噪声的增加，性能会下降。我们还发现InversionNet是最敏感的模型。
- 数据驱动方法和物理驱动方法之间比较：我们比较了两种方法的准确性和计算成本。当训练样本和测试样本的数量之比小于62时，数据驱动方法的反演结果要好得多，而且速度更快。
- 3D模拟和2D切片之间的比较：我们使用3D“Kimberlina-V1”数据集的2D速度/地震数据切片训练InversionNet，并与InversionNet 3D基准进行比较。结果是可比的，尽管InversionNet 3D的表现略好（0.9625与0.9838相比）。
- 在真实的场景中选择数据集：我们在[49]中选择一个真实的速度图并生成其他地震数据，然后应用在10个OpenFWI数据集上训练所有20个模型。仅在这种情况下，使用L1损失训练的最佳模型来自FlatVel-B，使用L2损失训练的最佳模型来着Style-A数据集。
6 讨论
6.1 Future Challenges—未来挑战
根据迄今为止所展示的结果，本文设想了数据驱动的FWI的四个未来挑战，OpenFWI应该能够增强相关研究的能力，如下所示：
- 复杂速度图的反演：地下复杂性高的数据集的性能恶化需要更先进的方法，特别是那些不依赖于更多数据的方法。
- 数据驱动方法的泛化：现场数据通常不同于训练数据集，因此良好的泛化对于现场应用中的数据驱动FWI至关重要。然而，现有的方法在遭受不可忽视的退化。我们期待更强大的方法来处理不同领域的数据。
- 计算效率：根据我们的经验，UPFWI和InversionNet3D遭受搞结算成本，这限制了它们的潜在应用。特别是对于InversionNet3D，训练数据是采用多个通道进行下采样的，这可能会导致信息的丢失和性能受到影响。对于这些方向的研究，预计会有更加有效的算法。
- 被动地震成像：本文的基准测试结果主要涵盖可控/主动震源成像问题，但被动地震问题也是一个很大的子领域。如何利用数据驱动和FWI方法解决主动成像问题还需要进一步的研究和发展。我们对被动数据的事件拾取进行了初步测试，可以在补充材料的第15节中找到，作为未来研究的启动实验。
6.2 Broader Impact—更广泛的影响
- 数据驱动的FWI：FWI是一个典型的科学问题，几十年来一直在用物理驱动的方法进行研究，随着深度学习的快速发展，我们已经看到了无数的数据驱动方法。OpenFWI拥抱这一结合点，并为社区带来了以下潜力：①统一评价、评估；②进一步改进；③再现性和完整性，随着这一主题研究的发展上述这些是必不可少的。我们还设想了OpenFWI支持领域专家们尝试以平稳的开始探索深度学习方法，以及机器学习专业人员寻求进一步改进当前的局限性。
- 未来发展：我们计划通过发布新的数据集和新的基准并为社区提供后续问题来精心维护OpenFWI。将有关于OpenFWI的未来更新的研讨会、以及在适当的交界处举办更具有挑战性的数据/任务的数据竞赛。我们也胃肠感谢物理学和机器学习社区对改进OpenFWI的任何反馈。
- 人工智能在科学中的应用：科学机器学习（SciML）正在包括地球科学在内的各种领域展现其巨大潜力。与机器学习的其他领域（如计算机视觉和自然语言处理）相比，仍然存在严重的数据挑战—稀疏的直接测量、数据分布不平衡、不可避免的噪声等。我们的努力有望为SciMl克服这些数据挑战提供一些帮助，以便在典型的科学丰富和数据匮乏的科学领域取得令人兴奋的进展。
7 结论
在本文中介绍了OpenFWI，这是一个开源平台，包括12个数据集和四种深度学习的基准测试。发布的数据集具有各种尺度，涵盖了地球物理学的不同领域，并模拟了地下结构的多种场景。目前的基准在一些数据集上显示出有希望的结果，而其他数据集上还需要进一步改进。此外，我们还包括复杂性分析、泛化研究和不确定性量化，以证明我们数据集和基准的有利特性。最后，我们讨论了可以用这些数据集研究的现有挑战，并设想了随着OpenFWI的发展，未来的发展。
———————————————————————————————————————————
附录安排：
- 附录A强调了支持可重复性的公共资源，并描述了OpenFWI数据和发布代码的许可证。
- 附录B展示了速度图的生产流程。
- 附录C展示了地震正演模拟的配置。
- 附录D介绍了数据集文件的格式、命名的做法和其他细节。
- 附录E显示了网络架构的设计并指定了所涉及的参数。
- 附录F提供了用于训练的所有参数和配置以保证重现性。
- 附录G包含所有数据集的预测速度图的更多插图。
- 附录H介绍了地下复杂性的度量，并给出了具体的数值结果和说明。
- 附录I展示了关于泛化测试结果和分析的更多细节。
- 附录J进行了不确定性量化的案例研究。
- 附录K包括稳健性分析以及如何提高模型的稳健性。
- 附录L比较了物理驱动方法和数据驱动方法的反演结果和计算成本。
- 附录M研究通过InversionNet预测2D切片是否可以具有与InversionNet 3D相当的结果。
- 附录N详细说明了真实世界情况下的测试策略。
- 附录O建立了OpenFWI与被动地质推断及其潜在应用的联系。
- 附录P对数据集以前的版本和OpenFWI的当前限制进行了更多讨论。
A OPENFWI Public Resources and Licenses
首先，OpenFWI基准的可重复性得到了一下一些公共资源的保证。值得注意的是，我们有一个小组（链接如下），欢迎任何有关的讨论。我们的团队还承诺维护平台，并根据社区反馈支持进行进一步的开发。
- Website: https://openfwi-lanl.github.io
- Dataset URL: https://openfwi-lanl.github.io/docs/data.html#vel
- Github Repository: https://github.com/lanl/openfwi
- Pretrained Models: https://tinyurl.com/bddzkxfz
- Tutorial: https://openfwi-lanl.github.io/tutorial/
- Google Group: https://groups.google.com/g/openfwi
根据美国洛斯阿拉莫斯国家实验室和能源部的要求，这些代码在OSS许可证和BSD-3许可证下在Github上发布。我们还将知识共享署名-非商业性使用-相同方式共享4.0国际许可证附加到数据中。
B Velocity Map Generation（未完）
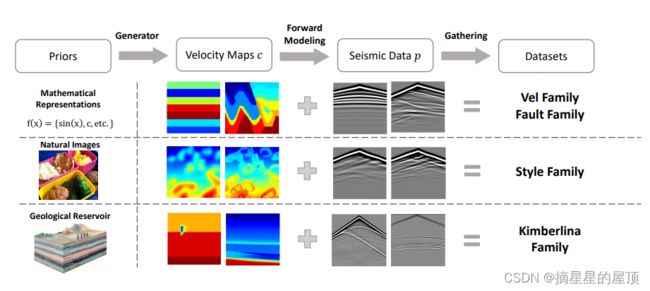
在本节中，我们将介绍数据的生成情况。基本上，数据生成遵循两个步骤：①合成速度图c ②经正演建模生成地震数据p。在第一步中，我们从三种不同的先验信息生成速度图：数学公式、自然图像和地质储层，这对数据集有显著贡献。
图8：数据生成介绍。从三个不同的先验建立速度图c，然后经由正演建模生成地震数据p。收集速度图c和地震数据p以构成四个数据集系列。
C Seismic Forward Modeling Details（未完）
D OPENFWI Datasets: Illustration, Format, Naming, Loading—OpenFWI数据集：插图、格式、排版与加载（未完）
E OPENFWI Benchmarks: Network Architecture（待理解与修改）
OpenFWI基准测试基于四种深度学习方法：InversionNet[20]、VelocityGAN[27]和UPFWI[31]用于2D FWI，InversionNet 3D[30]用于3D FWI。这些方法的所有细节可以从他们的原始论文中找到。而在本节中，我们将特别描述OpenFWI数据集采用的网络架构。请注意，“Vel”、“Fault”和“Style”系列中的十个数据集具有相同的大小，因此共享相同的网络架构。Kimberlina-CO2数据需要对卷积核参数进行微小更改。
E.1 InversionNet
InversionNet是一个编码器-解码器结构的CNN网络。编码器提起洗澡输入的超特征，解码器根据压缩的特征向量估计相应的速度图。我们在编码器中堆叠了14个CNN层，其中第一层的内核大小为7×1，下面的六层的内核大小为3×1。每隔一层应用stride步幅2将独居维度减少到速度图维度。然后使用六个3×3的CNN层来提取压缩数据中的时空特征，其中使用stride步幅2每隔一层对数据进行下采样。之后，堆叠一个内核大小为8×9的CNN层，将特征图展平为输出潜在向量大小，在我们的实验中为512。解码器首先在潜在向量上应用反卷积层生成的具有5核大小的5×5×512的张量，然后具有相同数量的输入和输出通道的卷积层。反卷积-卷积过程中在饭卷积层中以4的内核大小重复4次，从而产生大小为80×80×32的特征图。最后，我们通过一个70×70的窗口对特征图进行中心裁剪，并应用一个3×3的卷积层来输出一个单通道速度图。因此，编码器中有14个CNN层，减去中有11个层。前面提到的卷积层和饭卷积层转之后会进行批归一化，并使用LeakReLU作为激活函数。
E.2 VelocityGAN
VelocityGAN是一个生成式对抗网络，其中生成器与InversionNet中的编码器-解码器网络具有相同的架构。它具有9层的CNN。首先，使用8个3×3的CNN层来提取速度图中的时空特征，其中使用步幅2每隔一层对数据进行下采样。然后，使用内核为5×5且填充为零的CNN层作为输出层。同样，上述所有卷积层之后都会进行批量归一化和LeakReLU作为激活函数。为了训练GAN，我们使用Wasserstein 损失，除了pixel-wise L1-norm和L2norm外，我们还使用Wasserstein 损失和梯度损失来区分真实和生成的速度图。
E.3 UPFWI（代理解）
UPFWI是一种无监督学习方法，它利用编码器-解码器架构中的卷积层。一般的网络架构与InversionNet中的网络架构相同，除了解码器使用最近邻上采样的CNN层作为反卷积层。
与其他基准方法不同，UPFWI通过以下损失函数最小化数据差异：
E.4 InversionNet 3D
作为InversionNet在3D领域的自然扩展，InversionNet3D以类似的拓扑结构构建。最浅的版本（本文中的结果就是从其中获得的）构建在编码器和解码器的13层上，每一层都是3D卷积或反卷积，然后是批量归一化和LeakyReLU激活。为了减少内存消耗和计算复杂度，特意选择了3D FWI的两个最重要的障碍，即过滤器的大小和每一层的步幅，另外在网络的某些阶段采用了两个特殊的组件，组卷积与可逆层。因此，这个基线网络有1442万个参数，并消耗9.93GB的内存，批量大小为1。建议参考原始论文，以获得对网络架构更准确和详细的描述。
F OPENFWI Benchmarks: Training Configurations—OpenFWI基准：训练配置
在本节中，我们提供了训练配置的详细信息，以保证可再现性。所有实验都在NVIDIA Tesla P100 GPU上实现。我们已经通过Google Drive发布了预训练模型：https://tinyurl.com/bddzkxfz。代码和相关信息可以在Github上找到： https://github.com/lanl/OpenFWI。
在2D基准测试中，我们在InversionNet和VelocityGAN的所有数据集上使用相同的参数，而UPFWI的训练在不同的数据集上略有不同。特别的，我们使用AdamW作为优化器，权重衰减为
，动量参数
，
来更新所有模型。对于InversionNet，学习率为，并且不应用衰减。mini-batch的大小为256。我们为所有的InversionNet训练了120个epoch。对于VelocityGAN，生成器和学习器的学习率都是，并且没有应用衰减。mini-batch的大小设置为64。遵循[57]的策略，我们在每次生成器更新时执行三次迭代。所有VelocityGAN模型都经过了480个epoch的训练。
对于UPFWI，初始学习率为
，我们在第150和175个时期将学习率降低了10倍，除了在CurveVel-A和CurveVel-B上的实验没有应用衰减，在CurveVel-A和CurveVel-B上的实验中，mini-batch的大小为128，在其他所有的实验中为256.我们遵循[31]，并将每个损失项的权重设置为1。由于相对较高的计算成本，我们尽可能多地训练UPFWI模型。在不同的实验中，epoch的数量从200到500不等。在3D基准测试中，我们在所有实验中都保持了和InversionNet 3D相同的训练配置，详细信息可以在[30]中找到。
在训练过程中，我们应用最小-最大归一化将速度图和地震数据重新缩放为[-1,1]。速度值在1500~4500 m/s之间。对于“KimFamily”，Kimberlina-CO2中的速度范围在947~2545 m/s，3D Kimberlina-V1中的速度值范围为1975 ~ 3892 m/s。
G Illustration of Inversion Results—反演结果演示
基准采用SSIM反演结果的数值评估。在这里，我们在图14至图17中所有数据集上展示了不同方法的说明。我们注意到VelocityGAN通常提供最好的结果。UPFWI使用预测和观测地震数据之间的差异作为损失函数，因此它对层的边界敏感，这是数据中反射波的原因。此外，由于地震资料的有线下，UPFWI难以对速度图的深部进行反演。
图14：“Vel”系列中地面实况与反演结果示例。 左侧展示了地面真实速度图，右侧显示了使用InversionNet、VelocityGAN和UPFWI的反演结果。从第一列到最后一行：FlatVel-A、FlatVel-B、CurveVel-A、CurveVel-B。
H Velocity Map Complexity—速度图复杂度
在本节中，我们介绍了用于策略速度图复杂度的单个度量：空间信息[58]、梯度稀疏指数[59]和香农熵[60]。香农熵是“信息量”的最广泛应用的量化器，根据定义，它是数据集中变量对数的期望。空间信息（SI）是边界幅度的估计值，因为它是从Sober算子[61]获得的，Sober算子是一种边缘检测滤波器。梯度稀疏指数（GSI）也通过应用sober算子来计算图像中非平滑像素的百分比。具体来说，设
和
表示通过Sober滤波器获得的水平和垂直坐标（x,y）上的梯度大小，G表示以
为像素p上的元素的矩阵，p表示像素的总数，然后我们有以下定义：
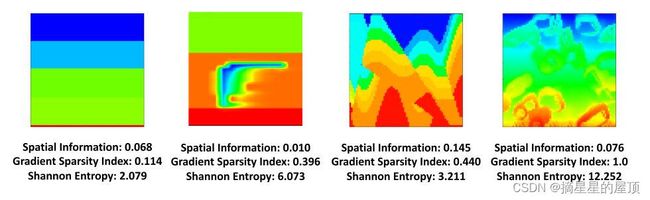
速度图复杂性的度量加深了我们对数据集的理解，并有望成为研究人员选择合适数据集的指导。数值计算结果见表8。为了更直观，图18展示了速度图及其复杂性的三个度量值。根据复杂性、基准测试结果和我们的经验，初学者可以从简单的数据集（FlatVel-A、FlatVel-B、CurveVel-A、FlatFault-A、Curve-Fault-A和Kimberlina-CO2）中受益，而高级解决方案应该在具有挑战性的数据集（CurveVel-B、FlatFault-B、CurveFault-B、Style-A和Style-B）上进行评估。
我们从表8中得到了一些观察结果。首先，对于每个数据集，这三个指标基本上是一致的。其次，版本B中的数据集总是比版本A具有更高的复杂性，这符合我们的期望，即版本B是硬版本。第三，具有曲线结构的数据集显示出比具有平坦结构的相应数据集更高的复杂性（例如CurveVel-A与FlatVel-A）。其次，版本B中的数据集总是比版本A具有更高的复杂性，这符合我们的期望，即版本B是困难版本。第三，具有曲线结构的数据集显示出比具有平坦结构的相应数据集更高的复杂性（例如CurveVel-A与FlatVel-A）。
表8：2D数据集的速度图复杂度（空间信息、梯度稀疏指数、香农熵）
图18：每个数据集系列中不同级别的速度图复杂性示例。
这种测量的主要局限性是：这三个指标都不能在所有数据集上提供一致的评估。例如，虽然“Style Family”数据集比“Vel”和“Fault”族数据集具有更复杂的细节，这与Shannon熵一致，但我们不能从空间信息中暗示它。我们注意到，差异是由于数据生成方法的差异。简而言之，我们强调，尽管我们可以通过三个指标之间的交叉引用来证明数字结果的合理性，但最好是进行一次利用所有三个指标的综合分析。
I Generalization Test
在本节中，我们分别在表9至表11中提供了对InversionNet、VelocityGAN和UPFWI进行泛化测试的详细结果。“FVA”是FlatVel-Ad缩写，相同的命名跪着适用于其余数据集。蓝色、橙色和绿色框分别表示具有“Vel”系列、“Fault”系列和“Style”系列的域内测试。对于所有这三种反演方法，下方三角形项的值始终大于上方项，除了InversionNet具有一些离群值。VelocityGAN和UPFWI的性能优于InversionNet，这与[31，27]中的结果一致。此外，InversionNet使用比其他两种方法更大的批量大小，这可能会降低其泛化能力。
表9：使用InversionNet测试10个2D数据集的泛化性能。蓝色、橙色、绿色框表示具有“Vel”系列、“Fault”系列和“Style”系列的域内测试。
表10： 使用VelocityGAN测试10个2D数据集的泛化性能。蓝色、橙色、绿色框表示具有“Vel”系列、“Fault”系列和“Style”系列的域内测试。
表11：使用UPFWI测试10个2D数据集的泛化性能。蓝色、橙色、绿色框表示具有“Vel”系列、“Fault”系列和“Style”系列的域内测试。
J Uncertainty Quantification—不确定性度量
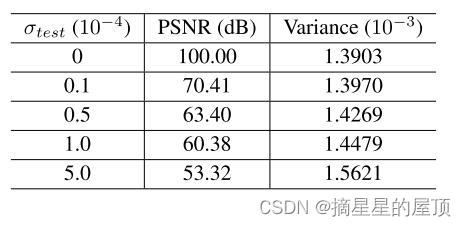
我们进一步在CurveVel-A上进行实验，以量化INversionNet中的不确定性作为案例研究。在[62]之后，我们修改了网络架构，在除最后一个卷积层之外的每个卷积层之后添加了一个丢失率p=0.2的丢失层来修改网络体系结构。如图19所示，边界上的不确定性高于其他区域，这意味着边间周围的预测灵敏度更高。为了量化不确定性和边界之间的相关性，我们计算不确定性值和边缘上的梯度幅度之间的Pearson相关性。该值为0.5462，表示中度正相关，如图20所示。如表12所示，当噪声水平增加时，不确定性逐渐增加。我们还将平均峰值信噪比（PSNR）包括在表中。样本的PSNR定义为：
其中，
和
表示数据集中地震数据的最大和最小可能值，
是干净的地震数据，而
是噪声数据。同时，交叉数据集的不确定性远高于在泳衣数据集上进行训练和测试。表13表明域转移导致不确定性增加。
图19： 不确定性可视化。与其他区域相比，边界上的不确定性更高。
图20：平均方差与速度边缘梯度幅度之间的相关性。
表12：关于噪声地震输入的不确定性量化的定量结果。在检验过程中，将不同标准差的高斯噪声加入到地震数据中（
）
表13：2D数据集平均方差的定量结果。该模型在CurveVel-A上训练。
K Robustness Test（未完）
L Comparison with Physics-driven Methods（未完）
M Comparison between InversionNet and InversionNet3D—InversionNet和InversionNet 3D的比较（未完）
在本节中，我们将InversionNet3D数据作为2D切片处理时的性能与InversionNet 3D的基准性能进行比较。将地球视为二维平面式处理真实数据的常用方法。为了量化2D和3D训练策略之间的差异，我们执行了以下两个2D实验，并将其结果与3D Kimberlina-V1数据集上的InversionNet 3D基准测试结果进行了比较。
N Test Strategy in Real-world Situation（未完）
O Passive Picking
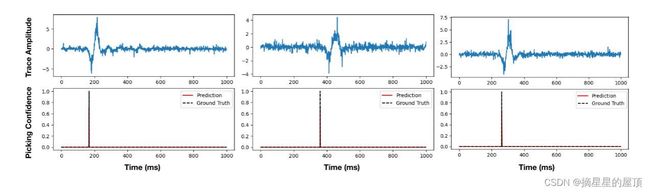
目前的OpenFWI数据集主要关注主动或受控震源的地球物理成像问题，这意味着震源通常是受控爆炸或由振动器产生的。然而，还有另外一个地球物理成像问题的致力于，被动地震成像，其中源项是未知的。它是全球地震学、水力压裂检测、页岩油气勘探、二氧化碳注入检测和许多其他研究领域的干苔外套。其主要目的实在给出一个可靠的速度模型时，找到被动震源的信息，包括震源的空间位置、起始点和地震矩张量。OpenFWI对被动地震问题的潜在贡献是使用提供的大量模拟道来训练神经网络。例如，PhaseNet[69]，该神经网络可以进行波至拾取或事件检测，这是被动地震成像问题的重要步骤。本文以P波的波达拾取为例。我们通过向地震道添加（a）P波到达的标签和（b）强高斯噪声（
）来转换“Style-B”数据集。然后，我们训练一个InversionNet来预测噪声地震道中的P波到达。相应的测试结果图29所示，这表明在转换后的数据集上训练的InversionNet可以准确地识别P波的到达。此外，OpenFWI数据集都作为未知数，尽管它们都位于顶面，并在FWI方案[70,71]或神经网络中反演源或者速度模型。在未来的 OpenFWI版本中，我们可能会在数据可用性和DOE、LANL批准的情况下开源被动地震数据集和基准。
图29：在Style-B数据集上训练的InversionNet的P波到达拾取。人工生成并在培训阶段使用到训练标签。
P Discussion
P.1 Past Version—过去版本
我们注意到，在以前的出版物中已经使用了几个同名的数据集。具体来说，FlatVel-A和CurveVel-A首先出现在[20]中；FlatFault-A和CurveFault-A在[31]中产生，Style-A和Style-B在[21]中提出。OpenFWI统一了“Vel”、“Fault”和“Style”系列中的所有数据集的数据大小和正演建模参数，以及基准测试结果的训练参数。因此，与以前报道的实验结果略有不同。从OpenFWI，我们将保持现在提供的数据集，未来的比较也应该与OpenFWI基准进行。
P.2 Limitations—限制
OpenFWI数据集：所有数据集都是从少数先验知识（即，数学表示、自然图像或地质储层），因此将固有地限制所生成的速度图的代表性和可变性。我们还注意到，在一般情况下，“Style”系列数据集是野外数据反演的优秀候选者。然而，可能有一些特定的地下结构没有被OpenFWI覆盖。此外，如果OpenFWI可以与一些现场数据进行验证，以进一步评估，将是更好的。
OpenFWI基准测试：当前的基准测试主要有2个测试。第一，3D FWI的文献有限，我们的基准几乎是孤立的。此外，我们的评估策略测试时随机选择的通道，因此是不普遍的。另外一个问题时，数据驱动的FWI已经随着新的进步而蓬勃发展，由于相关代码的不可用，我们可能无法比较所有其他最新的方法。
以下是关于我的一些思考：
9 常用关键术语
| 英文 | 中文 |
| Full Waveform Inversion（FWI） | 全波形反演 |
| Partial Differential Equations（PDEs） | 偏微分方程 |
| Convolutional Neural Networks（CNNs） | 卷积神经网络 |
| Generative Adversarial Networks（GANs） | 生成对抗性网络 |
| Geologic Carbon Sequestration（GCS） | 地质固碳 |
| Scientific Machine Learning（SciML） | 科学机器学习 |
| Peak-to-noise Ratio（PSNR） | 峰值信噪比 |
10 思考
- 多尺度是什么意思？
- 如何使用香农熵判断地层的复杂性？
- 损失函数之间的区别？
- 什么表示域内测试？本文中域内测试的结果可以得出什么结论？
- 最近邻上采样是什么意思？