unity-shader-2
个人学习使用,摘抄《unity shader 入门》一书中部分重要内容
创建 shader
在 unity 中使用 shader (手写):
-
创建材质,创建 shader ,将 shader 应用于材质
-
创建物体(需要有 meshrender、meshfliter 组件),将材质应用于物体
-
在材质面板中,调整 shader 属性改变物体外观
创建 shader 时的预设:
- 包含标准光照模型的表面着色器(和光源打交道)
- 不含光照 (含雾效) 的顶点 / 片元着色器(光源较少、需要自定义渲染效果)
- 实现屏幕后处理效果的模板
- 利用GPU并行性进行一些计算的模板
- 包含光线追踪相关计算的模板
还可以通过 shader graph 图形界面来创建 shader ,两种创建方法在 unity 内部作用的一致。
shaderLab
unity 为方便用户写 shader 专门提供的一种语言——shaderLab 格式类似 JSON :
一个 shader 包括自身信息、子着色器 SubShader 和默认着色器 Fallback 三部分
// shader 名称
Shader "Custom/ToonShader" {
Properties {
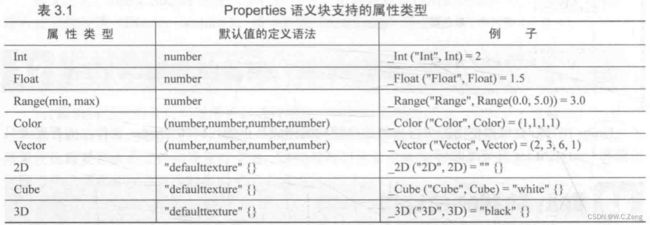
// 属性的名字(用于 shader 计算应用各种效果) 显示在面板上的名字(用于提示用户方便调整各种效果) 属性的类型(数据类型)
// 支持的类型 int float range color vector 2d cube 3d
_Color ("Color", Color) = (1,1,1,1)
}
SubShader {
// 显卡A使用的子着色器 的代码
// 可选的标签
Tags { "RenderType"="Opaque" }
// 可选的状态
Cull Front
ZWrite Off
// 代表一次渲染流程
Pass {
// 定义名称
Name "OUTLINE"
// 定义 Pass 在 unity 渲染流水线中的角色
Tags{ "LightMode" = "Always" }
}
}
SubShader {
// 显卡B使用的子着色器
[Tags]
[RenderSetup]
Pass {
[Name]
[Tags]
[RenderSetup]
}
}
// 当显卡无法执行以上任何一个着色器时,默认使用的着色器
FallBack "Diffuse"
}
表面着色器是 unity 提供的对顶点/片元着色器的一种抽象(本质上自动会转化为顶点/片元着色器),自动处理光照细节,让用户方便快捷地使用 shader
定义在 subshader 语句块中,而非 pass 语句块,在 CGPROGRAM 关键字与 ENDCG 之间(使用CG/HLSL语言编写)。
Shader "..." {
SubShader {
Tags {}
CGPROGRAM
#pragma surface surf Lambert
struct Input {
float4 color : COLOR;
};
void surf(Input IN, inout SurfaceOutput o) {
o.Albedo = 1;
}
ENDCG
}
}
片元/顶点 着色器定义在 pass 语句块中
Shader "..." {
SbuShader {
Pass {
CGPROGRAM
// 编译指令
#pragma vertex vert
#pragma fragment frag
float4 vert(float4 v : POSITION) : SV_POSITION {
return mul (UNTY_MATRIX_MVP, v);
}
fixed4 frag() :SV_Target {
return fixed4(1.0,0.0,0.0,1.0);
}
ENDCG
}
}
}
上述两种都是较新的可编程管线,较旧的设备可能不支持,就需要使用固定函数着色器。
unity 中,模型空间使用左手坐标系
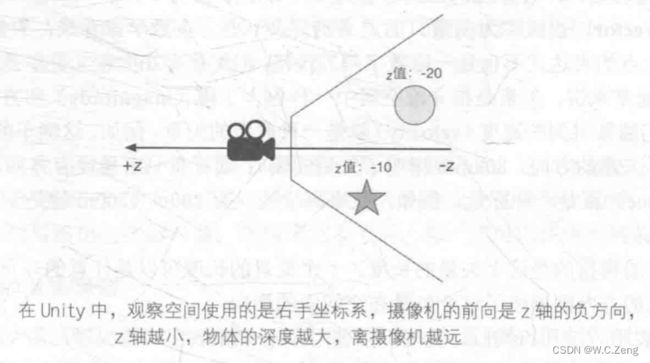
观察空间使用右手坐标系,相机沿着 -Z 方向看,Z 值越小,离摄像机越远
数学基础
笛卡尔坐标系(原点、两或三条垂直的轴)、点和向量
左手坐标系和右手坐标系
矢量和标量、矢量乘除标量、三角形法则、矢量的模
方向向量、归一化、点积和叉积
点积的意义:投影、向量之间夹角的余弦(判断玩家是否处于敌怪前方的视角范围)
点积的性质:点积与标量乘法结合、点积与矢量加减结合、自身的点积等于模的平方
叉积的意义:得到同时垂直于两个向量的新向量(法向量)、向量之间夹角的正弦、判断三角形面朝里还是朝外(根据左手坐标系、三个顶点逆时针排列时三角形面朝向正前方)
矩阵
用来描述矢量的坐标空间转换、矢量的位置变换
把矢量转化成行矩阵或列矩阵,参与矩阵的运算,就能得到变换后的矢量(在unity中把矢量转化为列矩阵,放在最右边参与矩阵的运算,阅读时从右往左阅读,矢量使用矩阵进行变换)
矩阵和标量的乘法、矩阵和矩阵的乘法(新矩阵的每个元素Cij的值,等于原矩阵A中i行和B中j列矢量的点积)
特殊的矩阵
方阵(又叫方块矩阵,行列数目相同)、对角矩阵(对角线上元素不为0,其余元素为0的方阵)、单位矩阵(对角线上元素为1,其余为0的方阵)、转置矩阵(行列交换、串接再转置等于转置再反向串接)
逆矩阵(首先得是方阵,然后它与原矩阵的乘积为单位矩阵)
如果矩阵有逆矩阵,它就是可逆的(非奇异的)(行列式不为0);否则它就是不可逆的(奇异的)。
逆矩阵的性质:逆矩阵的逆矩阵是它本身、单位矩阵的逆矩阵是它本身、转置再求逆等于求逆再转置、串接再求逆等于求逆再反向串接
正交矩阵:矩阵和它的转置矩阵乘积为单位矩阵,那么这个矩阵就是正交矩阵(结合逆矩阵的定义,我们发现正交矩阵的转置等于正交矩阵的逆矩阵)
矩阵与它的转置矩阵乘积的结果的行矢量是单位矢量、且互相垂直时(矩阵行列之间构成一组标准正交基矢量),那它就是一个正交矩阵。P60
变换
用矩阵表示变换
线性变换:可以保留矢量加法、矢量与标量乘法的变换,定义变换
f ( x ⃗ + y ⃗ ) = f ( x ⃗ ) + f ( y ⃗ ) f ( k x ⃗ ) = k f ( x ⃗ ) \mathbf{f}(\vec{x}+\vec{y}) = \mathbf{f}(\vec{x}) + \mathbf{f}(\vec{y})\\\mathbf{f}(k\vec{x})=k\mathbf{f}(\vec{x}) f(x+y)=f(x)+f(y)f(kx)=kf(x)
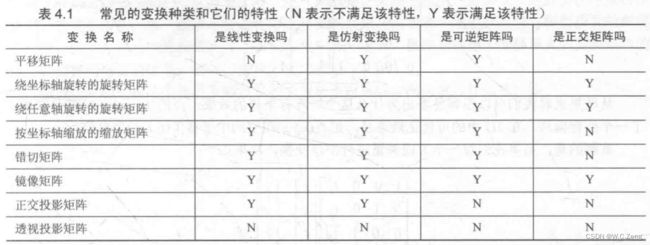
线性变换包括:缩放、旋转、错切、镜像、正交投影,都可以 3 x 3 的矩阵表示
但是平移变换不能
因此引入仿射变换,仿射变换就是合并了线性变换和平移变换的变换类型,把矢量扩展到了四维空间用 4 x 4 的矩阵表示,这就是齐次坐标空间
因此需要把原先的三维向量转换为四维向量,这就是齐次坐标(可以超过四维)
对于原先的一个点,转化为四维坐标时,w 值为 1;对于原先的方向矢量,转化为四维坐标时,w 值为 0
平移矩阵、缩放矩阵、旋转矩阵(与GS101图形学入门中的变换矩阵相同,故省略)
大多数情况下,我们约定组合变换的顺序是:先缩放,再旋转,最后平移
unity 中绕多个轴旋转时的顺序为 zxy
坐标变换
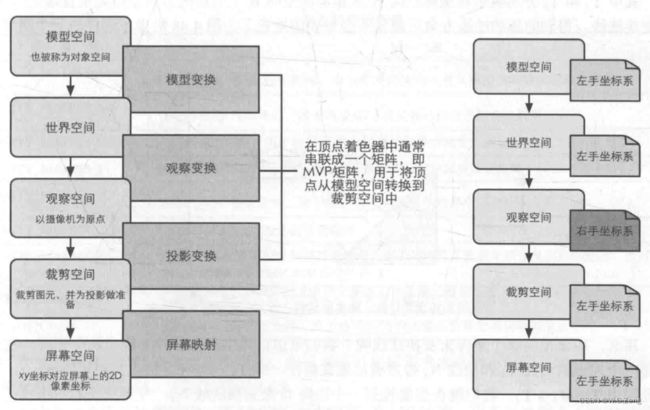
顶点着色器阶段时,模型的顶点坐标要从模型空间,转换到齐次裁剪坐标空间中(单位正方体空间)
模型空间 model space:又称对象空间、局部空间,是和对象有关的独立坐标空间,unity中模型空间使用左手坐标系
世界空间 world space:最外层的坐标空间,用于描述绝对位置,左手坐标系
观察空间 view space:又称摄像机空间,摄像机为原点,在unity中摄像机后方为+Z轴、右方为+X轴、上方为+Y轴
观察空间使用右手坐标系,符合 OpenGL 标准,摄像机正前方为-Z轴
将模型坐标从世界空间转换到观察空间时,由于从左手坐标系转换到右手坐标系,需要对 z 分量取反,就是再乘上一个特殊矩阵 [ 1 0 0 0 0 1 0 0 0 0 − 1 0 0 0 0 0 ] \left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&0\end{matrix}\right] ⎣ ⎡1000010000−100000⎦ ⎤ 来得到最终结果 P76
裁剪空间 clip space :由摄像机可以看到的空间,视锥体决定的空间。视锥体由 6 个平面包围而成,又叫裁剪平面。其中,近裁剪平面和远裁剪平面决定摄像机能看到的深度范围。
视锥体有两类分别对应两种投影类型:正交投影和透视投影
为了更通用的表示两种投影,我们先将顶点从观察空间转换到裁剪空间(这一步就是投影变换)中,之后根据 6 个裁剪平面的坐标进行裁剪(判断物体是否可见、部分可见)。
顶点进行正交投影后,w分量仍为1;进行透视投影后,w分量为-z。
屏幕空间:由像素点组成的二维空间。从裁剪空间变换到屏幕空间,需要经过齐次除法,得到归一化的设备坐标(在标准立方体中的坐标,OpenGL是[-1,1]的坐标范围,directX是[0,1]的坐标范围,unity使用OpenGL的规范)。
unity 中,屏幕坐标系左下角是 (0,0) ,将上述的 [-1,1] 坐标范围经过缩放,映射到 (0,0) ~ (screenWidth,screenHeight) 就能得到像素坐标
整个渲染流水线中,顶点经过了哪些坐标变换?P70
M–模型变换、V–观察变换(视图变换)、P–投影变换、屏幕映射(视口变换)
法线变换
模型的顶点往往带有法线信息,用变换矩阵变换顶点和大部分方向向量没问题,但是变换法线时可能出现问题。例如在进行非统一缩放变换时,变换后的法线不再垂直。因此需要一个新的矩阵来变换法线。
首先,法线垂直于切线,又因为切线可以由两个顶点之间的差值计算,那么我们就可以拿变换后的切线来算出法线
推导过程省略,最后的结论就是,原变换矩阵的逆转置矩阵可以用来变换法线,得到正确的结果。P87