矩阵分解程序及报告:LU分解、QR分解、Householder变换、Givens变换、URV分解
简介:
本博客包含了矩阵分解的LU、QR(Gram-Schmidt)、Orthogonal Reduction (Householder reduction 和Givens reduction)和 URV程序实现。
目录
文章目录
- 简介:
- 目录
- 1. LU分解
-
- 1.1 分解需满足的条件
- 1.2分解得到的矩阵的性质
- 1.3 程序实现思路
- 1.4 例子
- 1.5 程序代码
- 2. QR分解
-
- 2.1 格拉姆-施密特正交化算法
-
- 2.1.1 分解满足的条件
- 2.1.2 分解得到的矩阵满足的性质
- 2.1.3 程序实现思路
- 2.1.4 例子
- 2.1.5 程序代码
- 2.2 householder变换
-
- 2.2.1 分解满足的条件
- 2.2.2 分解得到的矩阵满足的性质
- 2.2.3 程序实现思路
- 2.2.4 例子
- 2.2.5 程序代码
- 2.3 Givens旋转
-
- 2.3.1 分解满足的条件
- 2.3.2 分解得到的矩阵满足的性质
- 2.3.3 程序实现思路
- 2.3.4 例子
- 2.3.5 程序代码
- 3. URV分解
-
- 3.1 分解满足的条件
- 3.2 分解得到的矩阵满足的性质
- 3.3 程序实现思路
- 3.4 例子
- 3.5 程序代码
- 4.可视化代码
- 5. 主函数
1. LU分解
1.1 分解需满足的条件
- N*N的可逆矩阵
- 列运算过程中,0不得在轴元位置
1.2分解得到的矩阵的性质
- L为单位下三角矩阵,U为上三角矩阵。
- 对于i=1,…,n, L i i L_{ii} Lii=1且 U i i U_{ii} Uii≠0。
- U是对A执行高斯消去法所得到的结果。
- L的主对角线下各元 L i j L_{ij} Lij,i>j,记录所执行的列取代运算的乘数。
当条件2得不到满足时补救方法是使用行交换运算设法产生其他非零轴元,将A=LU分解修改成PA=LU,其中P是排列矩阵。
1.3 程序实现思路
因为当P矩阵为单位矩阵时,PA=LU退化为A=LU,故可以将A=LU看成PA=LU的特殊情况,所有整个程序按照PA=LU的思路实现,首先读取矩阵检查矩阵是否为方阵,不是的话结束程序并输出报错信息,之后对输入矩阵进行高斯消元,在变换的同时将执行列取代运算的乘数记录到P矩阵中,因为采用PA=LU的思路,所以遇到0在轴元位置的情况时,直接采用行交换运算产生非零轴元,所以避免了不满足约束b的情况。完成高斯消元之后,如果得到的矩阵存在非零行,则说明输入矩阵A是不可逆的,程序结束并输出错误信息,如果矩阵A仍为可逆,则输出分解得到的P,L,U矩阵。
1.4 例子
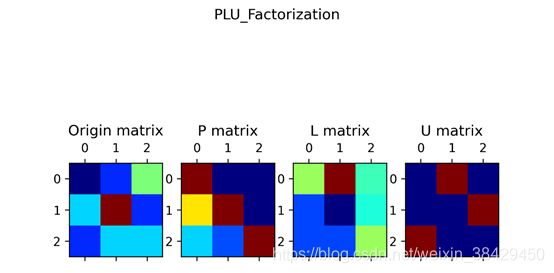
Sample1:
[[1.0, 2.0, 4.0], [3.0, 7.0, 2.0], [2.0, 3.0, 3.0]]
终端输出:
可视化:
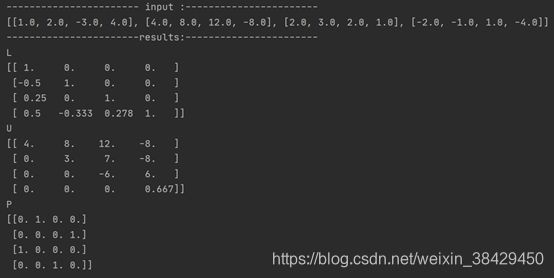
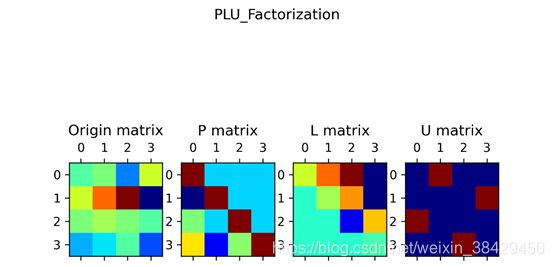
Sample2:
[[1.0, 2.0, -3.0, 4.0], [4.0, 8.0, 12.0, -8.0], [2.0, 3.0, 2.0, 1.0], [-2.0, -1.0, 1.0, -4.0]]
终端输出:
可视化:
1.5 程序代码
注:这个代码写得比较复杂,后面的代码会简介一些
import numpy as np
from visualization import visualization_PLU
def change_row(matrix,i,j):
'''
:param matrix: 输入矩阵
:param i,j:需交换的行
:return:
'''
temp=np.copy(matrix[i])
matrix[i]=matrix[j]
matrix[j]=temp
return matrix
def LU_Factorization(matrix):
'''
:param matrix: 输入矩阵
:param P L U: 分解得到的输出矩阵
:return:
'''
print("----------------------- input :-----------------------")
print(matrix)
matrix_copy=np.copy(matrix)
matrix=np.array(matrix)
row_len=matrix.shape[0]
col_len=matrix.shape[1]
#Premise1:suqare matrix
if(row_len==col_len):
#Solution step1: expand to an (matrix|b) matrix
order=list()
for i in range(row_len):
order.append(i)
order=np.array(order)
order=np.expand_dims(order,axis=0)
matrix=np.c_[matrix,order.T]
col_len+=1
#Solution step2: convert matrix to upper triangular form, and solve L, U, P
solution=np.zeros(matrix.shape)
show_matrix=np.zeros(matrix.shape)
col_index=0
for i in range(row_len-1):
if (col_index == row_len):
print( "ERROR: Your input is not invertible." )
exit( -1 )
pivot_row = i+np.argmax(np.abs(matrix[i:row_len, col_index]))
while(matrix[pivot_row,col_index]==0):
if(col_index<=row_len):
col_index+=1
else:
break
if(col_index==row_len):
print("ERROR: Your input is not invertible.")
exit(-1)
if(pivot_row!=i):
matrix=change_row(matrix,i,pivot_row)
solution=change_row(solution,i,pivot_row)
show_matrix = matrix+solution
for j in range(i+1,row_len):
if(matrix[j,col_index]!=0):
solution[j,col_index]=1.0*matrix[j,col_index]/matrix[i,col_index]
matrix[j,:row_len]=matrix[j,:row_len]-matrix[i,:row_len]*1.0*matrix[j,col_index]/matrix[i,col_index]
show_matrix = matrix+solution
col_index += 1
#Premise2:matrix is invertible
invertible=True
for i in range(row_len):
if((matrix[i,:col_len-1]==np.zeros(col_len-1)).all()):
invertible=False
if(invertible==True):
np.set_printoptions( precision=3, suppress=True )
U=matrix[:row_len,:row_len]
L=solution[:row_len,:row_len]
for i in range(row_len):
L[i,i]=1
P=np.zeros((row_len,row_len))
for i in range(row_len):
P[i][int(matrix[i,-1])]=1
print("-----------------------results:-----------------------")
print("L")
print(L)
print("U")
print(U)
print("P")
print(P)
#print("L:{}\n,U:{}\n,P:{}\n".format(L,U,P))
visualization_PLU(matrix_copy,L,U,P,title='PLU_Factorization')
else:
print("ERROR: Your input is not invertible.")
else:
print("ERROR:Your input is not a square matrix.")
2. QR分解
QR分解把矩阵分解成一个正交矩阵Q与一个上三角矩阵R的积。本博客中实现了三种QR分解的方法,分别是QR(Gram-Schmidt)、Orthogonal Reduction (Householder reduction 和Givens reduction),下面分别介绍:
2.1 格拉姆-施密特正交化算法
2.1.1 分解满足的条件
列向量无关的m*n矩阵
2.1.2 分解得到的矩阵满足的性质
Q为正交矩阵,R为上三角矩阵
2.1.3 程序实现思路
施密特正交化构建正交矩阵 Q ∈ R ( m × m ) Q∈R^{(m×m)} Q∈R(m×m)的方法是从A矩阵的n个列( A ( : , j ) ∈ R ( m × 1 ) A_{(:,j)}∈R^{(m×1)} A(:,j)∈R(m×1))中构建互相正交的基,先选定 A ( : , 0 ) A_{(:,0)} A(:,0) 为第一个基,然后把第二列 A ( : , 1 ) A_{(:,1)} A(:,1)减去平行于 A ( : , 0 ) A_{(:,0)} A(:,0) 的部分,剩下的垂直于 A ( : , 0 ) A_{(:,0)} A(:,0) 的部分作为下一个基,以此类推,直到生成了n个基,在构造完一个基之后还要用这个基的模长对其归一化。所以在程序中,对于输入矩阵,首先检查是否满足列向量无关的条件,然后再依次用上面的构造思路构造正交基。

2.1.4 例子
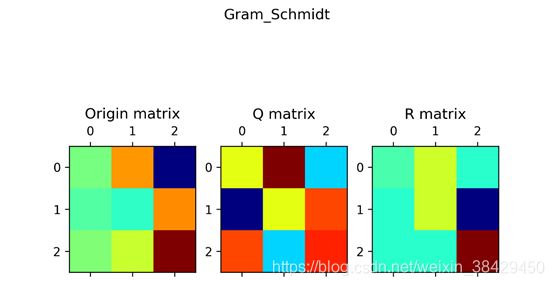
Sample1:
[[ 1. 19. -34.] [ -2. -5. 20.] [ 2. 8. 37.]]
终端输出:
可视化:
Sample2:
[[12.0, 3.0, 4.0], [5.0, 8.0, 0.0], [2.0, 1.0, 2.0]]
终端输出:
可视化:
2.1.5 程序代码
import numpy as np
from numpy.linalg import matrix_rank
from visualization import visualization_QR
def check(matrix):#考察能否完成QR分解的矩阵条件:所有列线性无关,即矩阵秩=列数
'''
:param matrix: 需分解矩阵
:return: 如果满足所有列线性无关则返回Ture,不满足返回False
'''
rank= matrix_rank( matrix )
n=matrix.shape[-1]
if(rank==n):
return True
else:
return False
def QR_Factorization(matrix):#斯密特正交化分解
'''
:param matrix: 需分解矩阵
:return: 正交矩阵Q,上三角矩阵R
'''
print(matrix)
np.set_printoptions( precision=3, suppress=True )
matrix=np.array(matrix)
if(check(matrix)==False):
print("输入矩阵各列不满足线性无关条件,请检查后重新输入!")
else:
Q = np.zeros_like(matrix)
count = 0
for a in matrix.T:
u=np.copy(a)
for i in range(0, count):
u=u-np.dot(np.dot(Q[:, i].T,a), Q[:, i]) #减去分量
norm_factor=np.linalg.norm(u) #归一化
Q[:, count]=u/norm_factor
count += 1
R = np.dot(Q.T,matrix)
print( "Q" )
print( Q )
print( "R" )
print( R )
visualization_QR( matrix, Q, R, title='Gram_Schmidt')#可视化
return (Q, R)
2.2 householder变换
2.2.1 分解满足的条件
任意N阶方阵
2.2.2 分解得到的矩阵满足的性质
N阶酉矩阵Q和N阶上三角矩阵R,其中酉矩阵满足以下性质:
1)它是埃尔米特矩阵: Q = Q ∗ Q=Q^* Q=Q∗
2)它是正交矩阵: Q ( − 1 ) = Q ∗ Q^{(-1)}=Q^* Q(−1)=Q∗
3)它也是对合的: Q 2 = I Q^2=I Q2=I
2.2.3 程序实现思路
Householder变换的通过将一个向量变换为由一个超平面反射的镜像实现,对于任意n维向量x,y,householder变换通过x和y之间的垂直平分面将x“反射”到y,因此可以利用householder变化将任意n维向量x变换成任意一个等长的若干个分量为0的向量,从而实现与高斯消元法相似效果。在程序中,通过将x矩阵反射为单位向量来实现该变换,其中householder变换构造方法为:
v = x − ∣ ∣ x ∣ ∣ 2 ∗ e 1 v=x-||x||_2*e_1 v=x−∣∣x∣∣2∗e1
ω = v / ∣ ∣ v ∣ ∣ 2 ω=v/||v||_2 ω=v/∣∣v∣∣2
H = I − 2 ω ω T H=I-2ωω^T H=I−2ωωT
2.2.4 例子
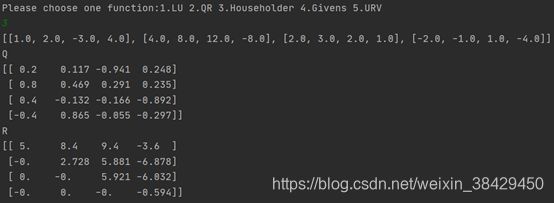
Sample1:
[[1.0, 2.0, -3.0, 4.0], [4.0, 8.0, 12.0, -8.0], [2.0, 3.0, 2.0, 1.0], [-2.0, -1.0, 1.0, -4.0]]
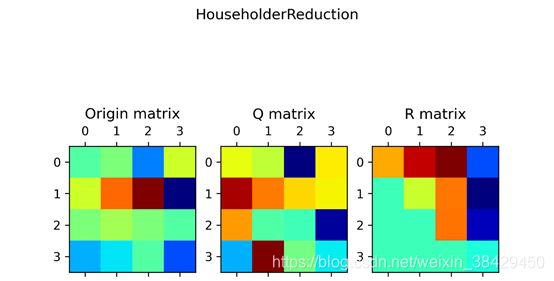
终端输出:
可视化:
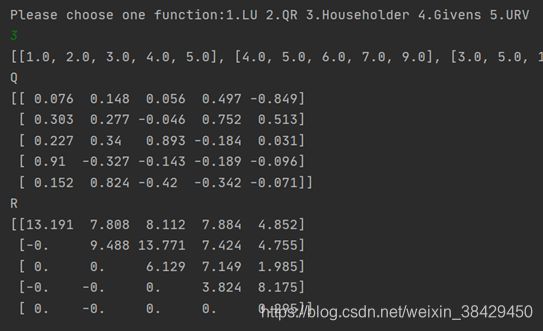
Sample2:
[[1.0, 2.0, 3.0, 4.0, 5.0], [4.0, 5.0, 6.0, 7.0, 9.0], [3.0, 5.0, 12.0, 10.0, 3.0], [12.0, 4.0, 2.0, 3.0, 1.0], [2.0, 9.0, 10.0, 3.0, 1.0]]
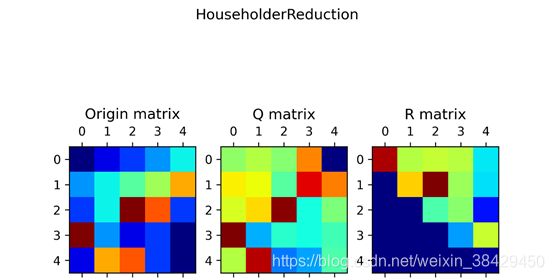
终端输出:
可视化:
2.2.5 程序代码
import numpy as np
from visualization import visualization_QR
import math
def Householder_Reduction(matrix):#Householder变换
'''
:param matrix: 需分解矩阵
:return: 酉矩阵Q,上三角矩阵R
'''
print(matrix)
np.set_printoptions( precision=3, suppress=True )
matrix=np.array(matrix)
row=np.shape(matrix)[0]
col=np.shape(matrix)[1]
P = np.identity( row )
T = np.copy( matrix )
for count in range( row - 1 ):
cur_col = T[count:, count]
e = np.zeros_like( cur_col )
e[0]=1
norm_factor=np.linalg.norm(cur_col)#归一化因子
u = cur_col - norm_factor*e#矩阵列向量-归一化因子*单位向量(变换构造第一二步)
factor=2.0*1/(u.T.dot(u))
I = np.identity( row )
I[count:, count:] -= (factor * np.dot(u[:, None], u.T[None, :]))#H=I-2ωω.T(变换构造第三步)
T = np.dot( I, T )
P = np.dot( P, I )
Q=P
R=T
print( "Q" )
print( Q )
print( "R" )
print( R )
visualization_QR(matrix,Q,R,"HouseholderReduction")#可视化
# print(np.dot(Q,R))
return (Q, R)
def Householder_Reduction_1(matrix):
"""
处理输入不为方阵的情况
:param matrix: 需分解的矩阵
:return: Q,R
"""
matrix= np.array(matrix)
m,n = matrix.shape
num = min( m , n ) - 1
if m > n :
num = num + 1
P = np.zeros((m,m,num))
Q = np.eye(m,m)
for i in range(m):
P[i, i, :] = 1
for i in range(num) :
e = np.zeros((m-i,1))
e[ 0 ,] = 1
I = np.eye( m - i , m - i )
u = np.reshape(matrix[ i : , i ],(m-i,1)) - np.reshape(math.sqrt(np.sum(matrix[ i : , i ] * matrix[ i : , i ])) * e,(m-i,1))
temp = I - 2*np.dot(u,u.T)/np.dot(u.T,u)
P[ i : , i : , i ] = np.copy(temp)
matrix = np.dot(P[ : , : , i ], matrix )
Q = np.dot(P[ : , : , i ], Q )
return matrix , Q.T
2.3 Givens旋转
2.3.1 分解满足的条件
任意N阶方阵
2.3.2 分解得到的矩阵满足的性质
Q为正交矩阵,R为上三角矩阵
2.3.3 程序实现思路
Givens变换是一种将n维向量x在第(i,k)两个维度确定的坐标平面内进行旋转,从而将其中一个分量化0的变换。因此有了 Givens 旋转方法,只要确定两个坐标之间的夹角,我们可以将任意向量旋转到单位向量上从而实现与高斯消元法类似的效果。其旋转矩阵的构建方法为:
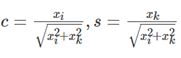
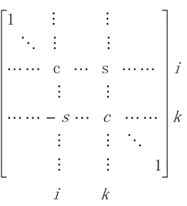
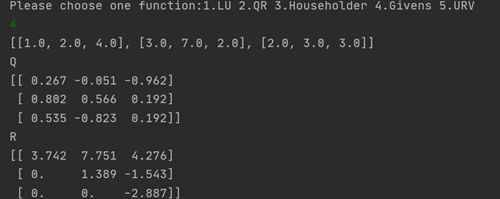
2.3.4 例子
Sample1:
[[1.0, 2.0, 4.0], [3.0, 7.0, 2.0], [2.0, 3.0, 3.0]]
程序输出:
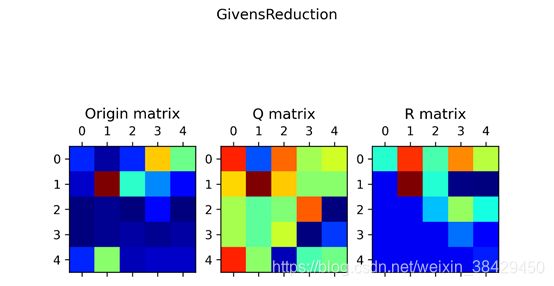
可视化:
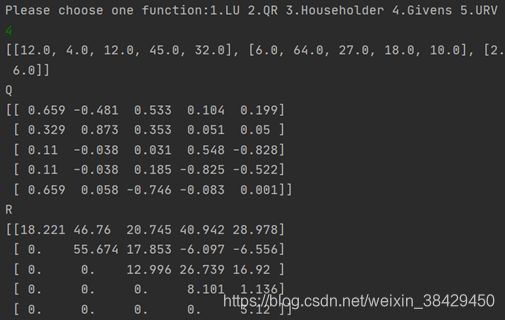
Sample2:
[[12.0, 4.0, 12.0, 45.0, 32.0], [6.0, 64.0, 27.0, 18.0, 10.0], [2.0, 3.0, 2.0, 10.0, 2.0], [2.0, 3.0, 4.0, 3.0, 4.0], [12.0, 34.0, 5.0, 6.0, 6.0]]
终端输出:
可视化:
2.3.5 程序代码
import numpy as np
from visualization import visualization_QR
def Givens_Reduction(matrix): #givens旋转
'''
:param matrix: 需分解矩阵
:return: 正交矩阵Q,上三角矩阵R
'''
print(matrix)
np.set_printoptions( precision=3, suppress=True )
row_len = np.shape( matrix )[0]
col_len = np.shape(matrix)[1]
P = np.identity( row_len )
T = np.copy( matrix )
for i in range( row_len ):
for j in range(col_len-1,i,-1):
val_a=T[i,i]
val_b=T[j,i]
mag = np.sqrt( (val_a ** 2 + val_b ** 2) )
#以下构建旋转矩阵
c = val_a / mag
s = val_b / mag
Pi = np.eye(row_len)
Pi[i, i] = c
Pi[j, j] = c
Pi[i, j] = s
Pi[j, i] = -s
#通过多个旋转矩阵相乘得到正交矩阵Q
P = np.dot(Pi,P)
T = np.dot(Pi,T)
Q = P.T
R = T
print( "Q" )
print( Q )
print( "R" )
print( R )
visualization_QR(matrix,Q,R,title="GivensReduction")
# print(np.dot(Q,R))
return (Q, R)
3. URV分解
3.1 分解满足的条件
任意矩阵
3.2 分解得到的矩阵满足的性质
若分解矩阵 A ∈ R ( m ∗ n ) A∈R^{(m*n)} A∈R(m∗n),则U为 m ∗ m m*m m∗m的正交矩阵,V为 n ∗ n n*n n∗n的正交矩阵, r a n k ( A ) = r rank(A)=r rank(A)=r,则 ( C r ∗ r 0 0 0 ) \left(\begin{array}{cc}C_{r * r} & 0 \\ 0 & 0\end{array}\right) (Cr∗r000)
3.3 程序实现思路
U的前r列时 R ( A ) R(A) R(A)的标准正交基
U的后(m-r)列是 N ( A T ) N(A^T) N(AT)的标准正交基
V的前r列是N 列是 R ( A T ) R(A^T) R(AT)的标准正交基
V的后(n-r)列是 N ( A ) N(A) N(A)的标准正交基
3.4 例子
sample:
[[-4. -2. 4. 2.] [ 2. -2. -2. -1.] [-4. 1. 4. 2.]]
终端输出:
可视化:
3.5 程序代码
import numpy as np
from Householder_Reduction import Householder_Reduction,Householder_Reduction_1
from numpy.linalg import matrix_rank
from visualization import visualization_URV
def URV_Factorization(matrix):#URV分解
'''
:param matrix: 需分解的矩阵
:return: m*m的正交矩阵U,V为n*n的正交矩阵V R为m*n的矩阵
'''
np.set_printoptions( precision=3, suppress=True )
Q_one,R_one =Householder_Reduction_1(matrix)
P = R_one.T
temp = Q_one[ : matrix_rank(Q_one), :]
Q_two,R_two = Householder_Reduction_1( temp.T )
Q = R_two.T
T = Q_two[ : matrix_rank(Q_two) , :]
R = np.zeros_like(matrix,dtype=float)
R[ : matrix_rank(Q_two) , : matrix_rank(Q_two)] = T.T
print( np.dot(np.dot(P.T,R),Q.T))
print("U")
print(P.T)
print("R")
print(R)
print("V")
print( Q.T)
visualization_URV(matrix, P.T, R, Q.T,title="URV_Factorization")
return P.T, R, Q.T
4.可视化代码
import numpy as np
import matplotlib.pyplot as plt
def visualization_PLU(A,B,C,D,title=None):
fig, axes = plt.subplots( nrows=1, ncols=4 )
axes[0].matshow( A, cmap='jet' )
axes[0].set_title( "Origin matrix" )
axes[1].matshow( B, cmap='jet' )
axes[1].set_title( "P matrix" )
axes[2].matshow( C, cmap='jet' )
axes[2].set_title( "L matrix" )
axes[3].matshow( D, cmap='jet' )
axes[3].set_title( "U matrix" )
plt.suptitle(title)
if(title!=None):
plt.savefig(title+'.png',dpi=300)
plt.show()
def visualization_QR(A,B,C,title=None):
fig, axes = plt.subplots( nrows=1, ncols=3 )
axes[0].matshow( A, cmap='jet' )
axes[0].set_title( "Origin matrix" )
axes[1].matshow( B, cmap='jet' )
axes[1].set_title( "Q matrix" )
axes[2].matshow( C, cmap='jet' )
axes[2].set_title( "R matrix" )
plt.suptitle(title)
if (title != None):
plt.savefig( 'QR_'+ title + '.png', dpi=300 )
plt.show()
def visualization_URV(A,U,R,V,title=None):
fig, axes = plt.subplots( nrows=1, ncols=4 )
axes[0].matshow( A, cmap='jet' )
axes[0].set_title( "Origin matrix" )
axes[1].matshow( U, cmap='jet' )
axes[1].set_title( "U matrix" )
axes[2].matshow( R, cmap='jet' )
axes[2].set_title( "R matrix" )
axes[3].matshow( V, cmap='jet' )
axes[3].set_title( "V matrix" )
plt.suptitle(title)
if(title!=None):
plt.savefig(title+'.png',dpi=300)
plt.show()
5. 主函数
import numpy as np
import copy
import sys
import matplotlib.pyplot as plt
from LU_Factorization import LU_Factorization
from QR_Factorization import QR_Factorization
from Householder_Reduction import Householder_Reduction
from Givens_Reduction import Givens_Reduction
from URV_Factorization import URV_Factorization
def ReadData(file_name):
f = open( file_name )
line = f.readline()
matrix=[]
while line:
line=line.strip('\n')
temp_line=line.split(" ")
temp_line=[float(x) for x in temp_line]
matrix.append(temp_line)
line = f.readline()
f.close()
return matrix
def choose_func(choose):
function={
'1':LU_Factorization,
'2':QR_Factorization,
'3':Householder_Reduction,
'4':Givens_Reduction,
'5':URV_Factorization,
}
method = function.get( choose )
if method:
file_name='./examples/example1.txt'
matrix=ReadData(file_name)
method(matrix)
else:
print("您的输入的选项有误,请检查后重新输入!")
if __name__ == '__main__':
print("Please choose one function:"
"1.LU "
"2.QR "
"3.Householder "
"4.Givens "
"5.URV ")
choose=input()
choose_func(choose)